Lý thuyết Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây – Toán 10 Cánh diều

Lý thuyết Toán 10 Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây - Cánh diều

A. Lý thuyết

I. Quy tắc cộng

Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n cách hoàn thành.

Ví dụ: Một nhóm học sinh ưu tú của lớp 10A có 13 học sinh nam và 7 học sinh nữ. Giáo viên muốn chọn ra 1 bạn để đi dự đại hội dành cho học sinh của khối. Hỏi giáo viên có bao nhiêu cách để chọn học sinh đó.

Hướng dẫn giải

Để chọn 1 học sinh ta thực hiện một trong hai hành động sau:

Chọn một học sinh trong 13 học sinh nam: Có 13 cách chọn.

Chọn một học sinh trong 7 học sinh nữ: Có 7 cách chọn.

Vậy có 13 + 7 = 20 cách chọn 1 học sinh.

Vậy giáo viên có 20 cách để lựa chọn một học sinh để đi dự đại hội.

Nhận xét: Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện, hành động thứ ba có p cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n + p cách hoàn thành.

Ví dụ: Nhà trường tổ chức cho học sinh tìm hiểu về các đề tài. Ban tổ chức đưa ra ba nội dung gồm: 5 đề tài về khoa học tự nhiên, 6 đề tài xã hội và 10 đề tài về môi trường và cuộc sống. Hỏi mỗi học sinh có bao nhiêu khả năng lựa chọn. Biết mỗi học sinh chỉ được chọn một đề tài.

Hướng dẫn giải

Mỗi học sinh chọn một đề tài, tức là mỗi học sinh thực hiện một trong ba hành động sau:

Chọn một đề tài trong 5 đề tài về khoa học tự nhiên: Có 5 cách chọn.

Chọn một đề tài trong 6 đề tài về xã hội: Có 6 cách chọn.

Chọn một đề tài trong 10 đề tài về môi trường và cuộc sống: Có 10 cách chọn.

Vậy có 5 + 6 + 10 = 21 cách chọn 1 đề tài.

Vậy mỗi học sinh có 21 khả năng lựa chọn một đề tài để tìm hiểu.

II. Quy tắc nhân

Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai thì công việc có m.n cách hoàn thành.

Ví dụ: Để đi từ nhà An đến nhà Minh có hai con đường để đi. Từ nhà Minh đến nhà Lâm có ba con đường để đi. Hỏi có bao nhiêu cách lựa chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.

Hướng dẫn giải

Việc lựa chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh là thực hiện hai hành động liên tiếp.

 –  Chọn con đường đi từ nhà An đến nhà Minh có 2 cách chọn;

 –  Chọn con đường đi từ nhà Minh đến nhà Lâm có 3 cách chọn.

Theo quy tắc nhân, ta có 2.3 = 6 cách chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.

Vậy có 6 cách chọn con đường đi từ nhà An đến nhà Lâm và đi qua nhà Minh.

Nhận xét: Một công việc được hoàn thành bởi ba hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có p cách thực hiện hành động thứ ba thì công việc có m.n.p cách hoàn thành.

Ví dụ: Một người ăn trưa tại một của hàng. Trong thực đơn có 5 món thịt, 3 món rau và 4 món tráng miệng. Hỏi người này có bao nhiêu cách để lựa chọn một bữa ăn gồm 1 món thịt, 1 món rau và 1 món tráng miệng.

Hướng dẫn giải

Để lựa chọn một bữa ăn có 1 món thịt, 1 món rau và 1 món tráng miệng thì phải thực hiện qua ba hành động liên tiếp là:

 –  Lựa chọn một món thịt: có 5 cách chọn.

 –  Lựa chọn một món rau: có 3 cách chọn.

 –  Lựa chọn một món tráng miệng: có 4 cách chọn.

Theo quy tắc nhân, ta có 5.3.4 = 60 cách chọn 1 món thịt, 1 món rau và 1 món tráng miệng.

Vậy người này có 60 cách để lựa chọn một bữa ăn gồm 1 món thịt, 1 món rau và 1 món tráng miệng.

III. Sơ đồ hình cây

Nhận xét:

 –  Sơ đồ hình cây (Hình 6) là sơ đồ bắt đầu tại một nút duy nhất với cách nhánh tỏa ra các nút bổ sung.

 –  Ta có thể sử dụng sơ đồ hình cây để đếm số cách hoàn thành một công việc khi công việc đó đòi hỏi những hành động liên tiếp.

Ví dụ: Bạn Diệp muốn mua một chiếc đồng hồ đeo tay. Biết đồng hồ có 3 loại mặt để lựa chọn: mặt vuông, mặt tròn, mặt elip; có 2 loại dây đồng hồ là: dây da màu đen, dây da màu nâu. Hỏi Diệp có bao nhiêu cách để lựa chọn một chiếc đồng hồ.

Hướng dẫn giải

Để lựa chọn một chiếc đồng hồ phải trải qua hai hành động: Lựa chọn mặt đồng đồ, sau đó ứng với mỗi cách lựa chọn mặt đồng hồ ta lại lựa chọn dây đồng hồ.

Khi đó, ta có sơ đồ hình cây mô tả các cách chọn một chiếc đồng hồ như sau:

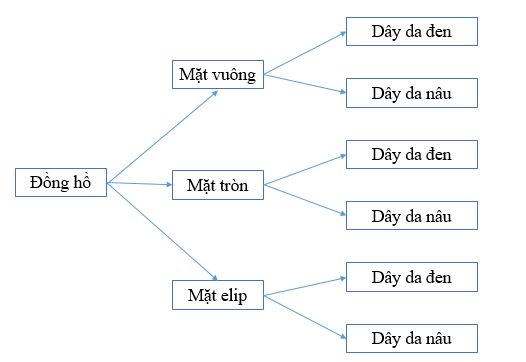
Quan sát sơ đồ hình cây ta thấy có 6 cách lựa chọn một chiếc đồng hồ.

Vậy có 6 cách để bạn Diệp lựa chọn 1 chiếc đồng hồ.

IV. Vận dụng trong bài toán đếm

Việc kiểm đến có ý nghĩa quan trọng trong toán học và thực tiễn, đặc biệt trong thống kê và xác suất. Kết quả đếm cho phép chúng ta xác định số khả năng mà một sự kiện có thể xảy ra để làm cơ sở cho việc đưa ra quyết định. Quy tắc cộng, quy tắc nhân và sơ đồ hình cây là những nguyên tắc cơ bản trong các bài toán đếm.

1. Vận dụng trong giải toán

Ví dụ: Cho 3 chữ số 3; 4; 5. Lập được bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau từ ba chữ số trên.

Hướng dẫn giải

Gọi số có ba chữ số đôi một khác nhau có dạng abc.

Để được một số có ba chữ số ta phải thực hiện 3 hành động liên tiếp.

 –  Chọn chữ số a: ta chọn một trong 3 chữ số {3; 4; 5}, có 3 cách chọn.

 –  Chọn chữ số b: chữ số b phải khác chữ số a, nên chữ số b có 2 cách chọn.

 –  Chọn chữ số c: chữ số c phải khác chữ số a và b nên chữ số c có 1 cách chọn.

Theo quy tắc nhân, ta có 3.2.1 = 6 cách chọn.

Vậy ta lập được 6 số tự nhiên có ba chữ số đôi một khác nhau từ ba chữ số {3; 4; 5}.

2. Vận dụng trong thực tiễn

Ví dụ: Bạn Mai muốn đặt mật khẩu cho điện thoại của mình bằng các chữ số. Biết mật khẩu là dãy số gồm 6 chữ số. Hỏi bạn Mai có bao nhiêu cách để đặt mật khẩu.

Hướng dẫn giải

Gọi mật khẩu cần đặt có dạng abcfeg.

Việc chọn mật khẩu là chọn liên tiếp 6 chữ số a, b, c, d, e, g mỗi chữ số là một trong các chữ số {0; 1; 2; …; 9}.

Chọn a: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.

Chọn b: là chọn 1 trong các chữ số {0;1; 2; …; 9}. Có 10 cách chọn.

Chọn c: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.

Chọn d: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.

Chọn e: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.

Chọn g: là chọn 1 trong các chữ số {0; 1; 2; …; 9}. Có 10 cách chọn.

Theo quy tắc nhân ta có 10 .10. 10. 10. 10. 10 = 1 000 000 cách đặt mật khẩu.

Vậy Mai có 1 000 000 cách để đặt mật khẩu.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Trong lớp có 30 học sinh trong đó 14 học sinh là nam. Giáo viên cần chọn 2 học sinh trong đó có 1 học sinh nam và 1 học sinh nữ để tham gia đội cờ đỏ. Hỏi giáo viên có bao nhiêu cách chọn.

Hướng dẫn giải

Lớp có 30 học sinh trong đó 14 học sinh là nam nên có 30 – 14 = 16 học sinh nữ.

Để lựa chọn 2 học sinh trong đó có 1 học sinh nam và 1 học sinh nữ ta thực hiện liên tiếp hai hành động sau:

 –  Chọn 1 học sinh nam, ta có 14 cách chọn.

 –  Chọn 1 học sinh nữ, ta có 16 cách chọn.

Theo quy tắc nhân, ta có 14.16 = 224 cách chọn hai học sinh 1 nam và 1 nữ.

Vậy giáo viên có 224 cách chọn hai học sinh 1 nam và 1 nữ để tham gia đội cờ đỏ.

Bài 2. Một cửa hàng có 4 loại sinh tố là: Sinh tố bơ, sinh tố mãng cầu, sinh tố dưa hấu, sinh tố xoài, và 3 loại nước ngọt là: coca cola, nước cam Twister; Mirinda. Hãy vẽ sơ đồ hình cây mô tả các cách chọn mua một loại sinh tố hoặc một loại nước ngọt ở cửa hàng này ?

Hướng dẫn giải

Để chọn mua một loại sinh tố hoặc một loại nước ngọt ở cửa hàng này ta thực hiện một trong hai hành động : Chọn mua một loại sinh tố hoặc chọn mua một loại nước ngọt. Ta có sơ đồ hình cây mô tả các cách lựa chọn như sau :

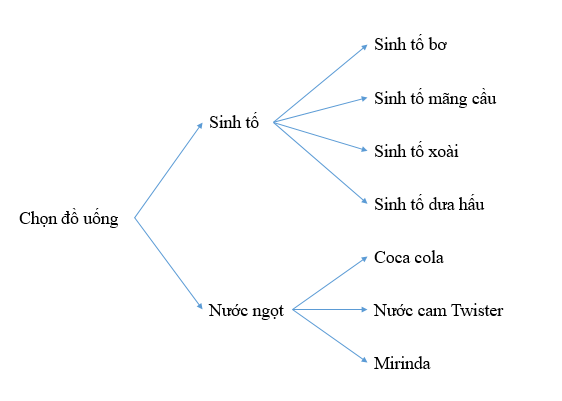
Từ sơ đồ hình cây ta thấy có 7 cách lựa chọn đồ uống.

Vậy có 7 cách chọn mua một loại sinh tố hoặc một loại nước ngọt ở cửa hàng này.

B.2 Bài tập trắc nghiệm

Câu 1. Có bao nhiêu số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị?

A. 40;

B. 45;

C. 50;

D. 55.

Hướng dẫn giải

Đáp án đúng là: B

Nếu chữ số hàng chục là n thì số có chữ số hàng đơn vị là n – 1. Do chữ số hàng chục lớn hơn hoặc bằng 1 còn chữ số hàng đơn vị lớn hơn hoặc bằng 0 nên ta có các trường hợp sau:

TH1: b = 0 thì a ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9}. Do đó có 9 số;

TH2: b = 1 thì a ∈ {2; 3; 4; 5; 6; 7; 8; 9}. Do đó có 8 số;

TH3: b = 2 thì a ∈ {3; 4; 5; 6; 7; 8; 9}. Do đó có 7 số;

...

TH9: b = 8 thì a = 9. Do đó có 1 số;

TH10: b = 9 thì không có a thỏa mãn.

Vậy số các số tự nhiên có hai chữ số mà các chữ số hàng chục lớn hơn chữ số hàng đơn vị là: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45 số.

Câu 2. Có 7 quả cầu đỏ khác nhau, 5 quả cầu vàng khác nhau và 3 quả cầu trắng khác nhau. Hỏi có bao nhiêu cách lấy 3 quả cầu có đủ ba màu.

A. 105;

B. 320;

C. 15;

D. 319.

Hướng dẫn giải

Đáp án đúng là: A

Vì chọn 3 quả cầu có đủ 3 màu nên mỗi màu ta chọn một quả

Quả cầu đỏ có 7 cách chọn

Quả cầu vàng có 5 cách chọn

Quả cầu trắng có 3 cách chọn

Vậy có 7 . 5 . 3 = 105 cách.

Câu 3. Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số?

A. 882;

B. 736;

C. 720;

D. 865.

Hướng dẫn giải

Đáp án đúng là: A

Gọi số có bốn chữ số cần tìm là $\overline{abcd}$, với a ≠ 0

Chọn số d có 3 cách chọn (vì số $\overline{abcd}$ là số lẻ nên d có thể chọn một trong 3 số là 1; 3; 5)

Chọn số a có 6 cách chọn (vì a ≠ 0 nên a có thể chọn một trong 6 số là 1; 2; 3; 4; 5; 6)

Chọn số b có 7 cách chọn (vì b chọn tuỳ ý nên b có thể chọn một trong 7 số là 0; 1; 2; 3; 4; 5; 6)

Chọn số c có 7 cách chọn(vì c chọn tuỳ ý nên c có thể chọn một trong 7 số là 0; 1; 2; 3; 4; 5; 6)

Số các số tự nhiên lẻ có 4 chữ số lập từ các số trên là: 3 . 6 . 7 . 7 = 882 (số).

Xem thêm tóm tắt lý thuyết Toán lớp 10 sách Cánh diều hay, chi tiết khác: