Lập phương trình của các mặt phẳng tọa độ (Oxy), (Oyz) và (Ozx)

Với giải bài tập 3 trang 80 sgk Toán lớp 12 Hình học được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

1 22,586 07/11/2024

Trang trước

Trang sau

Giải Toán 12 Bài 2: Phương trình mặt phẳng

Bài 3 trang 80 SGK Toán lớp 12 Hình học:

a) Lập phương trình của các mặt phẳng tọa độ (Oxy), (Oyz) và (Ozx).

b) Lập phương trình của các mặt phẳng đi qua điểm M(2; 6; –3) và lần lượt song song với các mặt phẳng tọa độ.

Lời giải:

a) Mặt phẳng (Oxy) là tập hợp các điểm có cao độ z = 0 nên có phương trình: z = 0.

Tương tự:

Mặt phẳng (Oyz): x = 0

Mặt phẳng (Ozx): y = 0.

b) Phương trình mặt phẳng đi qua M(2; 6; –3) và song song với (Oxy): z + 3 = 0

Phương trình mặt phẳng đi qua M(2; 6; –3) và song song với (Oyz): x – 2 = 0

Phương trình mặt phẳng đi qua M(2; 6; –3) và song song với (Ozx): y – 6 = 0.

*Phương pháp giải:

nhớ kĩ lý thuyết SGk

*Lý thuyết:

Phương trình tổng quát của mặt phẳng

1. Định nghĩa.

- Phương trình có dạng Ax + By + Cz + D = 0 trong đó A; B; C không đồng thời bằng 0 , được gọi là phương trình tổng quát của mặt phẳng.

- Nhận xét.

a) Nếu mặt phẳng (α) có phương trình Ax + By + Cz + D = 0 thì nó có một vecto pháp tuyến là $\vec{n} (A; B; C)$ .

b) Phương trình mặt phẳng đi qua điểm M (x₀; y₀; z₀) và nhận vectơ $\vec{n} (A; B; C)$ khác là vecto pháp tuyến là: A(x- x₀ ) + B( y – y₀) + C(z – z₀) = 0.

Trong không gian Oxyz, cho mặt phẳng (α) : Ax + By + Cz + D = 0.

a) Nếu D = 0 thì mặt phẳng (α) đi qua gốc tọa độ O.

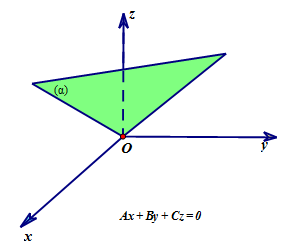
Lý thuyết Phương trình mặt phẳng chi tiết – Toán lớp 12 (ảnh 1)

- Nếu $A = 0, B \neq 0, C \neq 0$ thì mặt phẳng (α) song song hoặc chứa trục Ox.

- Nếu $A \neq 0, B = 0, C \neq 0$ thì mặt phẳng (α) song song hoặc chứa trục Oy.

- Nếu $A \neq 0, B \neq 0, C = 0$ thì mặt phẳng (α) song song hoặc chứa trục Oz.

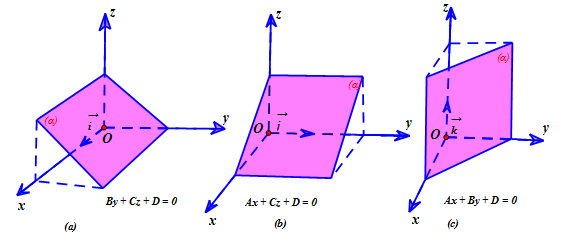
Lý thuyết Phương trình mặt phẳng chi tiết – Toán lớp 12 (ảnh 1)

- Nếu A = B = 0; $C \neq 0$ thì mặt phẳng (α) song song hoặc trùng với (Oxy).

- Nếu A = C = 0; $B \neq 0$ thì mặt phẳng (α) song song hoặc trùng với (Oxz).

- Nếu B = C = 0; $A \neq 0$ thì mặt phẳng (α) song song hoặc trùng với (Oyz).

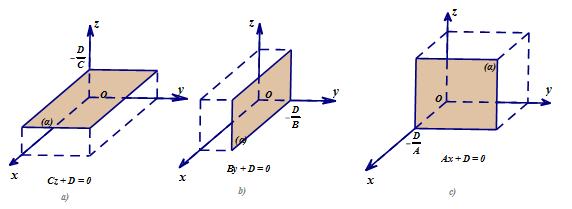
Lý thuyết Phương trình mặt phẳng chi tiết – Toán lớp 12 (ảnh 1)

- Nhận xét:

Phương trình mặt phẳng theo đoạn chắn $(α) : \frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$ . Ở đây (α) cắt các trục tọa độ tại các điểm (a; 0; 0); (0; b; 0); (0; 0; c) với $a b c \neq 0$ .