Trắc nghiệm Toán 8 Bài 6: Thể tích hình lăng trụ đứng
-
420 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
16/07/2024Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét.
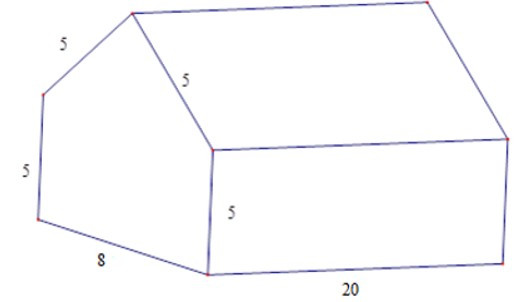
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Gọi H là trung điểm BC
=> AH ⊥ BC.
Ta có BH = 4; AB = 5 m
Bằng định lý Py-ta-go tính được
AH = = 3 m
Diện tích đáy của hình lăng trụ bằng:
S = 5.8 + = 52 (m2)
Thể tích nhà kho bằng:
V = 52.20 = 1040 (m3)
Câu 2:
19/07/2024Tính thể tích của hình lăng trụ đứng có chiều cao 20 cm, đáy là một tam giác cân có các cạnh bên bằng 5 cm và cạnh đáy bằng 8 cm.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
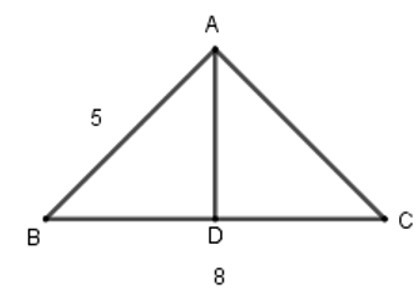
Gọi D là trung điểm của BC thì AD là trung tuyến cũng là đường cao trong tam giác
=> DB = DC = = 4 (cm) và AD ⊥ BC.
Tam giác ADC vuông tại D nên
AD2 + DC2 = AC2
AD2 + 42 = 52
AD = 9 AD = 3
Diện tích đáy S = = 12 (cm2).
Thể tích lăng trụ đứng là:
V = S.h = 12.20 = 240 cm3
Câu 3:
23/07/2024Cho lăng trụ đứng có kích thước như hình vẽ.
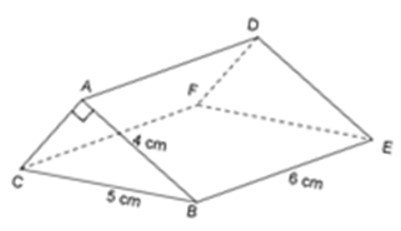
Số nào trong các số sau đây là thể tích của hình lăng trụ đứng đó?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
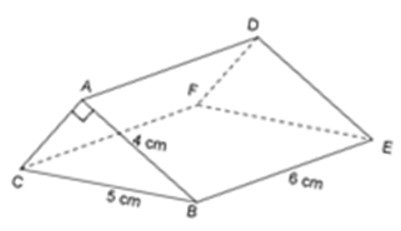
Hình lăng trụ đứng đã cho có đáy là một tam giác vuông.
Áp dụng định lý Pytago cho tam giác vuông ABC, ta có:
AB2 + AC2 = BC2 42 + AC2 = 52
AC2 = 52 – 42 = 9
=> AC = 3 cm.
Vậy diện tích đáy của hình lăng trụ đứng là:
S = SΔABC = AB.AC
= 3.4 = 6 cm2
Vậy thể tích của hình lăng trụ đứng là:
V = S.h = S.BE = 6.6 = 36 cm2
Câu 4:
22/07/2024Cho lăng trụ đứng có kích thước như hình vẽ.
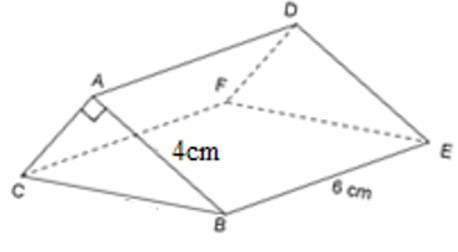
Biết thể tích hình lăng trụ bằng 36 cm3, độ dài cạnh BC là:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
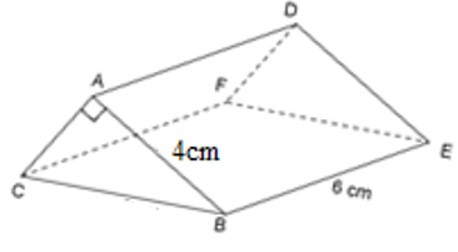
Diện tích tam giác ABC là:
S = 36 : 6 = 6 (cm2).
Độ dài cạnh AC là: = = 3 (cm).
Tam giác ABC vuông tại A nên
BC2 = AB2 + AC2 = 42 + 32 = 25
=> BC = 5 (cm)
Câu 5:
23/07/2024Tính thể tích của hình lăng trụ đứng có chiều cao 20 cm, đáy là một tam giác vuông có các cạnh góc vuông bằng 8 cm và 10 cm:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Vì đáy là tam giác vuông nên diện tích đáy
S = = 40 cm.
Thể tích lăng trụ đứng là
V = S.h = 40.20 = 800 cm3
Câu 6:
16/07/2024Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Hỏi công thức tính thể tích hình lăng trụ đứng là gì?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Công thức tính thể tích hình lăng trụ đứng là: V = S.h
Câu 7:
16/07/2024Một hình hộp chữ nhật có diện tích xung quanh bằng 100 cm2, chiều cao bằng 5cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Gọi a và b là các kích thước của đáy.
Ta có V = 5ab nên V lớn nhât
ab lớn nhất
Sxq = 100 nên 2 (a+b).5 = 120
hay a + b = 10
Ta có:
ab = a (10 – a) = -a2 +10a
= -(a – 5)2 + 25 ≤ 25
Suy ra V = 5ab ≤ 5.25 = 125.
Thể tích lớn nhất bằng 125 cm3 khi a = b = 5, tức là các cạnh đáy bằng 5 cm.
Câu 8:
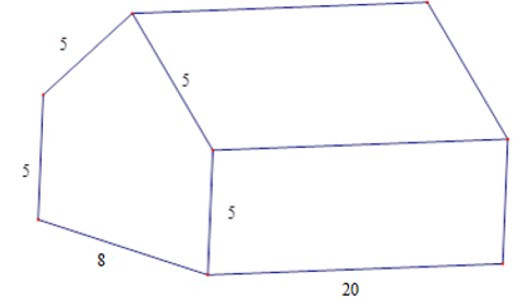
17/07/2024Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét.
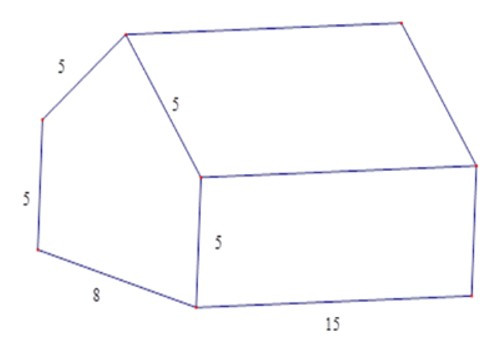
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
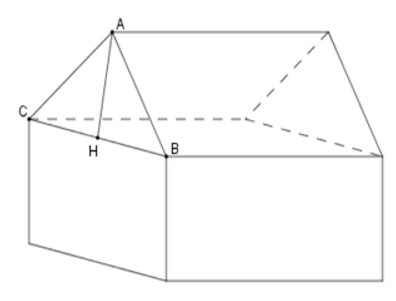
Gọi H là trung điểm BC
=> AH ⊥ BC.
Ta có BH = 4; AB = 5 m
Bằng định lý Py-ta-go tính được
AH = = 3 m
Diện tích đáy của hình lăng trụ bằng:
S = 5.8 + = 52 (m2)
Thể tích nhà kho bằng:
V = 52.15 = 780 (m3)
Câu 9:
22/07/2024Cho một hình lăng trụ đứng có thể tích V, diện tích đáy là S, chiều cao hình lăng trụ được tính theo công thức:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta có V = Sh => h =
Câu 10:
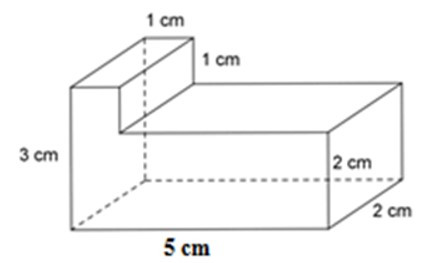
15/07/2024Tính thể tích của hình lăng trụ đứng sau:
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
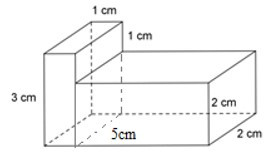
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là 3 cm, 1 cm, 2 cm; hình hộp chữ nhật thứ hai có kích thước là 2 cm; 4 cm; 2m.
Thể tích hình hộp chữ nhật thứ nhất là:
V1 = 3.1.2 = 6 cm3
Thể tích hình hộp chữ nhật thứ hai là:
V2 = 2.4.2 = 16 cm3
Thể tích hình lăng trụ đứng là:
V = V1 + V2 = 6 +16 = 22 cm3
Câu 11:
20/07/2024Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 3 cm, 8 cm. Chiều cao của hình lăng trụ đứng là 2 cm. Thể tích của hình lăng trụ đứng là:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
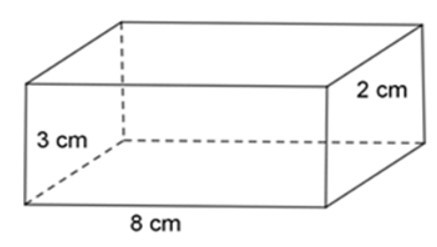
Thể tích của hình lăng trụ đứng là:
V = 8.3.2 = 48 cm3
Câu 12:
22/07/2024Một hình hộp chữ nhật có đường chéo bằng 3 dm, chiều cao 2 dm, diện tích xung quanh bằng 12 dm2. Tính thể tích của hình hộp chữ nhật.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
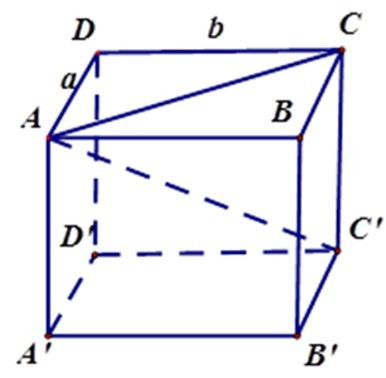
Hình hộp chữ nhật ABCD. A’B’C’D’
có AC’ = 3dm; CC’ = 2dm.
Xét tam giác ACC’ vuông tại C, theo định lý Pytago ta có
AC2 = C’A2 – C’C2
= 32 – 22 = 5
Vì diện tích xung quang là 12 dm2 nên chu vi đáy bằng 12 : 2 = 6 (dm)
Đặt AD = a, DC = b. Vì chu vi đáy là 6 dm
=> 2 (a + b) = 6
a + b = 3 (1)
và a2 + b2 = AC2 = 5 (2) (định lý Pytago cho tam giác vuông ADC)
Từ đó (1) và (2) suy ra a2 + (3 – a)2 = 5
Rút gọn được a2 – 3a + 2 = 0 hay (a – 1)(a – 2) = 0
Giả sử a ≥ b thì ta tìm được a = 2 suy ra b = 1.
Thể tích của hình hộp chữ nhật bằng 2.1.2 = 4 (dm3).
Câu 13:
22/07/2024Một hình hộp chữ nhật có diện tích xung quanh bằng 120 cm2, chiều cao bằng 6cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Gọi a và b là các kích thước của đáy.
Ta có V = 6ab nên V lớn nhât ab lớn nhất
Sxq = 120 nên 2 (a+b).6 = 120 hay a + b = 10
Ta có:
ab = a (10 – a) = -a2 +10a
= -(a – 5)2 + 25 ≤ 25
Suy ra V = 6ab ≤ 6.25 = 150.
Thể tích lớn nhất bằng 150 cm3 khi a = b = 5, tức là các cạnh đáy bằng 5 cm.
Câu 14:
18/07/2024Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 3 cm, 8 cm. Chiều cao của hình lăng trụ đứng là 2 cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
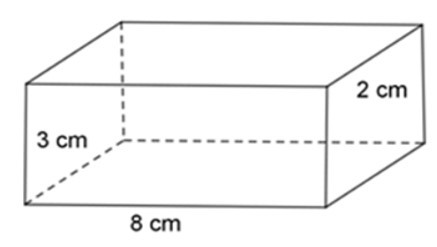
Diện tích xung quanh
Sxq = 2. (8 + 3).2 = 44 cm2
Thể tích của hình lăng trụ đứng là:
V = 8.3.2 = 48 cm3
Câu 15:
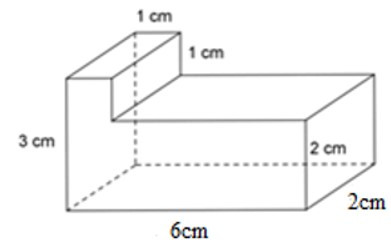
22/07/2024Tính thể tích của hình lăng trụ đứng sau:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
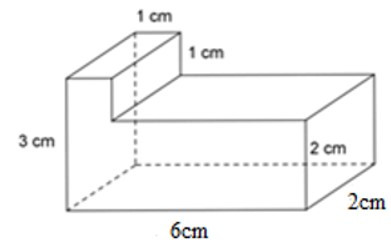
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là 3 cm, 1 cm, 2 cm; hình hộp chữ nhật thứ hai có kích thước là 2 cm; 5 cm; 2m.
Thể tích hình hộp chữ nhật thứ nhất là:
V1 = 3.1.2 = 6 cm3
Thể tích hình hộp chữ nhật thứ hai là:
V2 = 2.4.2 = 20 cm3
Thể tích hình lăng trụ đứng là:
V = V1 + V2 = 6 +20 = 26 cm3