Bài tập Hình chóp đều và hình chóp cụt đều (có lời giải chi tiết)
-
461 lượt thi
-
14 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Chọn phát biểu sai trong các phát biểu sau?
Xem đáp án
Áp dụng định nghĩa của hình chóp: Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh.
Phát biểu A sai.
Chọn đáp án A.
Câu 2:
15/07/2024Mặt bên của hình chóp cụt đều là hình gì?
Xem đáp án
Áp dụng định nghĩa của hình thang cân ta có: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Chọn đáp án C.
Câu 3:
21/07/2024Hình chóp tứ giác đều có mặt bên là hình gì?
Xem đáp án
Hình chóp tứ giác đều có mặt bên là tam giác cân.
Chọn đáp án A.
Câu 4:
15/07/2024Hình chóp lục giác đều có bao nhiêu mặt?
Xem đáp án
Hình chóp lục giác đều gồm có 6 mặt bên và 1 mặt đáy.
Chọn đáp án D.
Câu 5:
15/07/2024Hình chóp tam giác đều có đáy là?
Xem đáp án
Hình chóp tam giác đều có đáy là tam giác đều.
Chọn đáp án B
Câu 6:
01/11/2024Hình chóp ngũ giác đều có bao nhiêu mặt bên?
Xem đáp án
Đáp án đúng: A
*Lời giải
Hình chóp ngũ giác đều có đáy là ngũ giác đều và có 5 mặt bên.
*Phương pháp giải
- nắm lại kiến thức về hình chóp đều: số đỉnh, số mặt. số cạnh,...
*Lý thuyến cần nắm về hình chóp đều, hình chóp cụt đều:
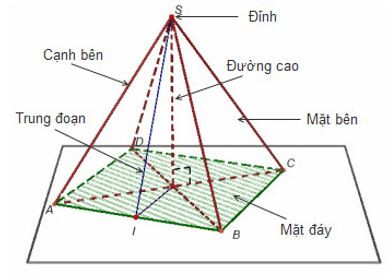
Hình chóp đều
Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh (là đỉnh của hình chóp).
+ Chân đường cao của hình chóp đều là tâm của đường tròn đi qua các đỉnh của mặt đáy.
+ Đường cao vẽ từ đỉnh của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
Hình chóp cụt đều
- Cắt hình chóp đều bởi một mặt phẳng song song với đáy. Phần hình chóp nằm giữa mặt phẳng đó và mặt đáy của hình chóp gọi là hình chóp cụt đều.
- Nhận xét: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
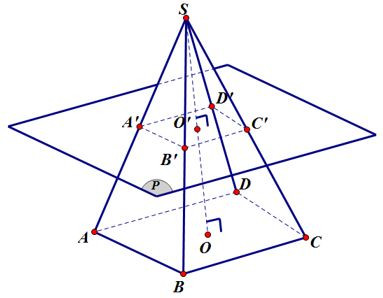
Hình trên có hình chóp cụt đều là ABCD.A’B’C’D’.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hình chóp đều và hình chóp cụt đều (mới + Bài Tập) – Toán 8
Toán 8 Bài 7 giải vở bài tập: Hình chóp đều và hình chóp cụt đều
50 Bài tập Hình chóp đều và hình chóp cụt đều Toán 8 mới nhất
Câu 7:
15/07/2024Hình chóp tứ giác đều có tất cả bao nhiêu mặt?
Xem đáp án
Hình chóp tứ giác đều có 4 mặt bên và 1 mặt đáy
Vậy có tất cả 5 mặt
Chọn đáp án C
Câu 8:
20/07/2024Hình chóp lục giác đều có bao nhiêu cạnh ?
Xem đáp án
Hình chóp lục giác đều có đáy là lục giác đều có 6 cạnh bằng nhau và có 6 cạnh bên.
Do đó, có tất cả 6 + 6 = 12 cạnh
Chọn đáp án D
Câu 9:
10/12/2024Cho hình chóp tứ giác đều. Chọn khẳng định sai
Xem đáp án
Đáp án đúng là D
Lời giải
Hình chóp tứ giác đều có:
+ Đáy là hình vuông.
+ Có 4 mặt bên và 1 mặt đáy. Nên có tất cả 5 mặt.
+ Số cạnh đáy là 4, số cạnh bên là 4 nên có tất cả 8 cạnh
*Phương pháp giải:
Nắm được lý thuyết chóp tứ giác đều
*Lý thuyết:
1. Khái niệm
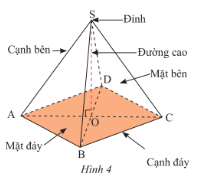
Hình chóp tứ giác đều có:
- Đáy là hình vuông.
- 4 cạnh bên bằng nhau.
- 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
- 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
- Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.
2. Công thức tính diện tích xung quanh của hình chóp tứ giác đều
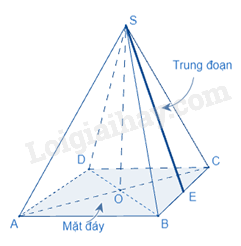
Diện tích xung quanh của hình chóp tam giác đều bằng nửa chu vi đáy với độ dài trung đoạn.
( là diện tích xung quanh, p là nửa chu vi đáy, d là trung đoạn)
3. Công thức tính thể tích của hình chóp tứ giác đều
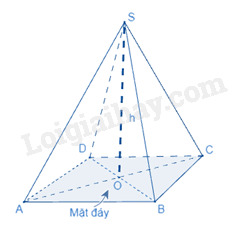
Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng diện tích đáy nhân với chiều cao.
(V là thể tích, là diện tích đáy, h là chiều cao)
Xem thêm
Câu 14:
16/07/2024Cho hình chóp tứ giác đều S.ABCD có đường cao SH = 6cm, cạnh đáy bằng 6cm. Lấy điểm H’ SH sao cho SH’ = . Một mặt phẳng đi qua H’ và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt ABCD.A’B’C’D’. Tính thể tích của hình chóp cụt ABCD.A’B’C’D’
Xem đáp án
Ta có: SH’ = SH = .6 = 4 (cm)
