Trắc nghiệm ôn tập Chương 4 Hình học: Hình lăng trụ đứng. Hình chóp đều (có đáp án)
Trắc nghiệm Toán 8 Bài ôn tập Chương 4 Hình học
-
448 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho hình lăng trụ đứng đáy là hình thoi có hai đường chéo lần lượt là 8cm và 10cm. Tính chiều cao của lăng trụ đứng biết thể tích của lăng trụ đứng là 360cm3.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Diện tích đáy hình thoi là:
12.8.10 = 40(cm2)
Vì V = Sd.h
=> h = VSd nên chiều cao của lăng trụ đứng là:
360 : 40 = 9(cm)
Câu 2:
23/07/2024Hình lăng trụ đứng tam giác có
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
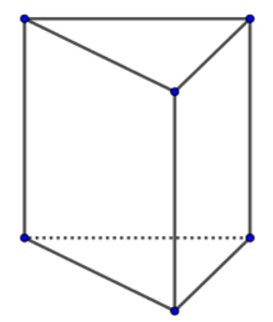
Quan sát hình vẽ ta thấy hình lặng trụ đứng tam giác có 5 mặt, 6 đỉnh và 9 cạnh.
Câu 3:
23/07/2024Cho hình lăng trụ đứng ABCD.A’B’C’D’, với mặt đáy ABCD là hình chữ nhật. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Vì ABCD.A’B’C’D’ là hình lăng trụ đứng có đáy là hình chữ nhật nên suy ra ABCD.A’B’C’D’ là hình hộp chữ nhật => AA’ = CC’ (cùng bằng BB’)
Câu 4:
18/07/2024Cho hình lăng trụ đứng ABCD.A’B’C’D’, với mặt đáy ABCD là hình chữ nhật. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Vì ABCD.A’B’C’D’ là hình lăng trụ đứng có đáy là hình chữ nhật nên suy ra ABCD.A’B’C’D’ là hình hộp chữ nhật => AA’ = CC’ (cùng bằng BB’)
Câu 5:
16/07/2024Hình chóp có 8 cạnh thì đáy là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Vì hình chóp có số cạnh gấp đôi số cạnh của đa giác ở đáy nên hình chóp có 8 cạnh thì đa giác đáy có 8 : 2 = 4 cạnh. Hay đáy là tứ giác.
Câu 6:
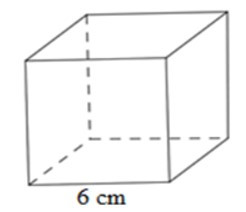
18/07/2024Thể tích của hình lập phương trong hình là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Thể tích hình lập phương V = 63 = 216cm3
Câu 7:
16/07/2024Hình lập phương là hình :
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Hình lập phương là hình có tất cả các mặt đều là hình vuông.
Câu 8:
16/07/2024Cho hình hộp chữ nhật ABCD.A’B’C’D’. Điểm M thuộc đoạn thẳng BD. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
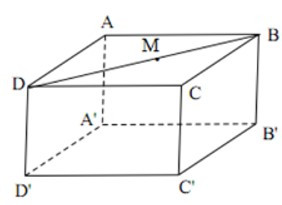
Vì M BD mà BD ⊂ (ABCD) nen M thuộc mặt phẳn (ABCD).
Câu 9:
23/07/2024Hình lăng trụ đứng tam giác ABC.A’B’C’. Cặp mặt phẳng dưới đây vuông góc
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Hình lăng trụ đứng tam giác có các mặt bên vuông góc với mặt đáy nên mp(ABB’A’) và mp(ABC) là hai mặt phẳng vuông góc.
Câu 10:
22/07/2024Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 8cm, đường cao SO = 10cm. Hỏi thể tích của hình chóp đều là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
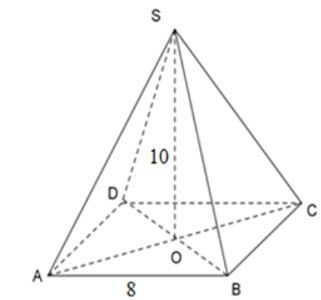
Tứ giác ABCD là hình vuông cạnh 8cm. Nên thể tích hình chóp tứ giác đều S.ABCD là
=> V = 13SABCD.SO
=13 .82.10 =6403 cm3
Câu 11:
23/07/2024Tính diện tích xung quanh của một hình lăng trụ đứng có đáy là hình ngũ giác đều cạnh 8cm, biết rằng chiều cao của hình lăng trụ đứng là 5cm.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Chu vi đáy của hình lăng trụ đứng là 8.5 (cm)
Diện tích xung quanh là:
Sxq = 8.5.5 = 2000 (cm2)
Câu 12:
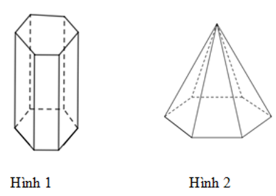
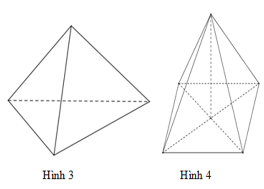
18/07/2024Quan sát các hình vẽ dưới đây và cho biết hình nào là hình chóp lục giác?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Hình 1 là hình lăng trụ có hai đáy là hai lục giác đều, hình 3 là hình chóp tam giác, hình 4 là hình chóp tứ giác.
Hình 2 là hình chóp lục giác vì có đáy là hình lục giác và các cạnh bên giao nhau tại một điểm.
Câu 13:
16/07/2024Cho hình hộp chữ nhật ABCD.EFGH. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
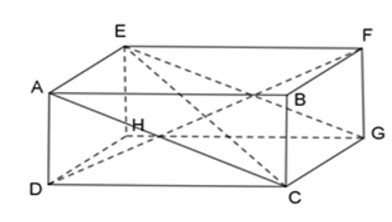
+) Ta có: AE // CG, AE = CG (gt)
Suy ra tứ giác ACGE là hình bình hành.
Mặt khác: AE ⊥ mp(EFGH))
Mà EG mp(EFGH)
=> AE ⊥ EG tại E.
Vậy tứ giác ACGE là hình chữ nhật nên A đúng.
+) Vì DH mp(EFGH) nên DH ⊥ HF tại H.
Áp dụng định lý Pitago cho tam giác DHF vuông tại H, ta có:
DH2 + HF2 = DF2 (1)
Vì AE ⊥ mp(ABCD) nên AE ⊥ AC tại A.
Áp dụng định lý Pitago cho tam giác EAC vuông tại A, ta có:
EA2 + AC2 = EC2 (2)
Mà DH = AE, HF = EG = AC (Hai đường chéo của hình chữ nhật) (3)
Từ (1), (2), (3) suy ra: DF2 = EC2
=> DF = CE nên B đúng.
Câu 14:
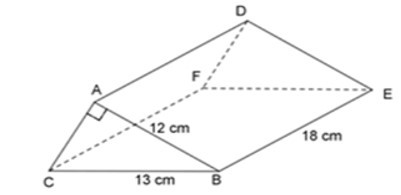
16/07/2024Cho lăng trụ tam giác dưới đây. Tính thể tích lăng trụ đó?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Áp dụng định lý Pitago vào tam giác ABC vuông tại A.
AB2 + AC2 = BC2
⇔ AC2 = BC2 - AB2
= 132 - 122 = 25
=> AC = 5cm
Vậy thể tích của hình lăng trụ đã cho là:
V = Sd.h = 12AC.AB.BE
= 12.5.12.18 = 540cm2
Câu 15:
20/07/2024Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều, M là trung điểm của BC, AA’ = AM = a. Thể tích của lăng trụ bằng:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
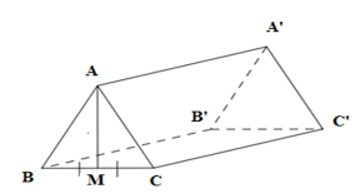
Vì tam giác ABC là tam giác đều nên AM vừa là trung tuyến vừa là đường cao của tam giác ABC.
Gọi chiều dài của cạnh tam ggiasc ABC là x. (x > 0)
=> BM = MC = x2,
AB = AC = BC = x
Xét tam giác vuông MAC, ta có:
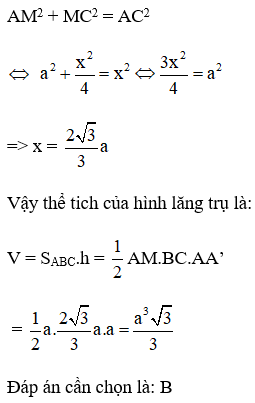
Câu 16:
17/07/2024Hình hộp chữ nhật ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a và diện tích hình chữ nhật ADC’B’ bằng 2a2, diện tích xung quanh của hình hộp chữ nhật bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Ta có ADC’B’ là hình chữ nhật
=> SADC’B’ = AD.DC’ = 2a2
=> a.DC’ = 2a2 => DC’ = 2a
Xét tam giác vuông CC’D ta có:
CC’2 + CD2 = C’D2
⇔ CC’2 + a2 = (2a)2
⇔ CC’2 = 4a2 - a2 = 3a2
=> CC’ = a√3
Vậy diện tích xung quanh của hình hộp chữ nhật là:
Sxq = 2.p.CC’
= 2.4a2.a√3=4a2√3
Câu 17:
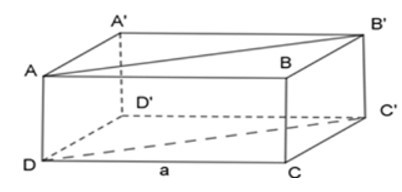
19/07/2024Cho hình hộp chữ nhật ABCD.A’B’C’D’. Tính diện tích hình chữ nhật ADC’B’ biết AB = 28cm, B’D2 = 37099, DD’ = 45cm.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
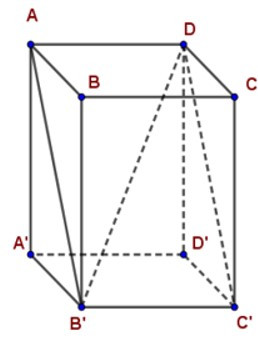
Xét tam giác AA’B’ vuông tại A’ có: AA’ = DD’ = 45cm và A’B’ = AB = 28cm
Áp dụng định lý Pytago ta có:


Câu 18:
23/07/2024Tính thể tích của hình chóp tứ giác đều có chiều cao là 4cm và độ dài cạnh đáy là 3cm
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Hình chóp tứ giác đều thì có đáy là hình vuông.
Do vậy, hình chóp có diện tích đáy là 32 = 9cm
Thể tích của hình chóp đều là:
V = 13S.h = 13.9.4 = 12(cm3)
Câu 19:
18/07/2024Tính diện tích xung quanh của hình hộp chữ nhật có bình phương độ dài đường chéo chính là 77; kích thước đáy là 4 và 6.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Gọi độ dài đường cao hình hộp chữ nhật là h (h > 0)
Ta có: h2 + 42 + 62 = 77
=> h2 = 25 => h = 5cm
Vậy diện tích xung quanh của hình hộp chữ nhật là:
Sxq = 2(4 + 6).5 = 100(cm2)
Câu 20:
18/07/2024Cho hình chóp tứ giác đều có các cạnh đáy dài 16cm và trung đoạn dài 20cm. Tính thể tích hình chóp. (làm tròn đến hàng phần trăm)
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
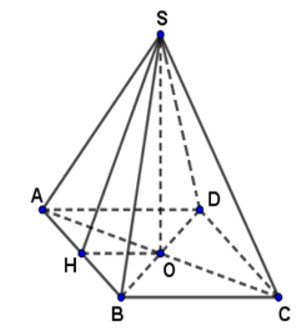
Xét hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh 16cm.
SO là đường cao SH là trung đoạn (H AB)
Vì SAB là tam giác cân nên H là trung điểm của AB.
O là giao điểm của hai đường chéo trong hình vuông ABCD nên O là trung điểm AC
Do đó, HO là đường trung bình trong tam giác ABC, suy ra HO = BC = 8cm
Xét tam giác SHO vuông tại O, Áp dụng định lý Pytago ta có:
SH2 = HO2 + SO2
=> SO2 =SH2 - HO2
=> SO = (cm)
Vậy thể tích hình chóp S.ABCD là
V = SO.SABCD
= .4.162 ≈ 1564,19cm3
Câu 21:
22/07/2024Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thang vuông ABCD vuông tại A, B (AB // BC) và BC = 12cm, AD = 16cm, CD = 5cm, đường cao AA’ = 6cm. Thể tích của hình lăng trụ là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
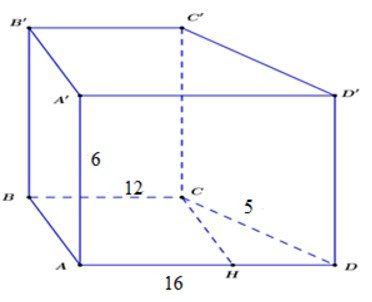
Trong mp (ABCD) kẻ CH vuông góc với AD tại H.
Khi đó ta có ABCH là hình chữ nhật. (do A = B = H = 900).
=> BC = AH = 12cm
=> HD = AD - AH = 16 - 12 = 4cm
Xét tam giác HCD vuông tại H ta có:
HC2 + HD2 = CD2 HC2
= CD2 - HD2 = 52 - 42
= 25 - 16 = 9
=> HC = 3 cm
Vậy thể tích của hình lăng trụ là:
V = SABCD.h = SABCD.AA’
=12 AA’.(BC + AD).CH
= 12.3.(12 + 16).6 = 252 cm3
Câu 22:
20/07/2024Cho hình lập phương ABCD.A’B’C’D’ có A’C = √3 . Tính thể tích của hình lập phương.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
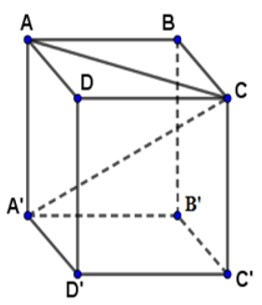
Xét hình lập phương ABCD.A’B’C’D’ có
A’C = AA’. √3= a√3
=> AA’ = a
Vậy thể tích hình lập phương là V = a3
Câu 23:
19/07/2024Tính diện tích toàn phần hình chóp tứ giác đều dưới đây:
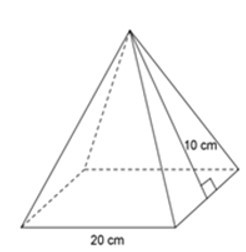
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
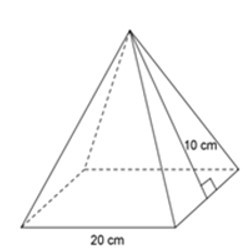
Mỗi mặt bên của hình chóp là tam giác có chiều cao 10cm và cạnh đáy 20cm.
Diện tích một mặt bên của hình chóp là
12.10.20 = 100(cm2)
Diện tích xung quanh hình chóp là
Sxq = 4.100 = 400(cm2)
Stp = Sxq + Sday
= 400 + 20.20 = 800cm2
Câu 24:
22/07/2024Cho hình chóp tam giác đều S.ABC có tất cả các cạnh bằng 2dm. Tính độ dài đoạn thẳng MN nối trung điểm 2 cạnh đối AB và SC.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
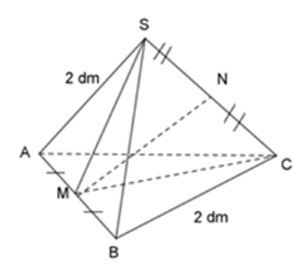
Theo đề bài ta có:
AM = MB = 12AB = 1dm
SN = NC = 12SC = 1dm
Ta có CM là đường trung tuyến của tam giác ABC.
Vì tam giác ABC là tam giác đều nên CM cũng là đường cao của tam giác ABC.
Áp dụng định lý Pitago vào tam giác CMB vuông tại M:
MC2 + MB2 = BC2
⇔ MC2 = BC2 - MB2 = 22 - 1 = 3
=> MC = √3dm
Tương tự ta xét tam giác vuông SMB, ta tính được: SM = √3dm
Xét tam giác SMC có
MS = MC = √3dm
=> Tam giác SMC là tam giác cân tại M.
=> MN vừa là đường trung tuyến vừa là đường cao của tam ggiacs SMC.
Áp dụng định lý Pytago cho tam giác MNC vuông tại N:
MN2 + NC2 = MC2
⇔ MN2 = MC2 - NC2 = 3 - 1 = 2
=> MN = dm
Câu 25:
18/07/2024Cho hình chóp cụt đều có 2 đáy là các hình vuông cạnh a và 2a, trung đoạn bằng a. Tính diện tích xung quanh của hình chóp cụt đều?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
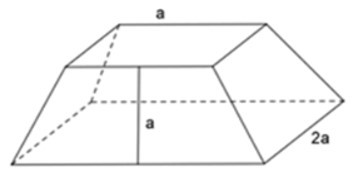
Hình chóp cụt đều có 4 mặt bên là các hình thang cân bằng nhau.
Suy ra, diện tích xung quanh của hình chóp cụt đều là tổng diện tích 4 hình thang cân, khi đó diện tích một mặt bên là
S =(a+2a).a2=3a22
Diện tích xung quanh hình chóp cụt đều là:
Sxq = 4. 3a22= 6a2
Câu 26:
18/07/2024Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SB = 5cm.
1. Tính bình phương đường cao SH của hình chóp.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
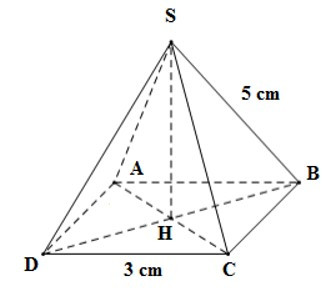
Lấy H là giao của 2 đường chéo hình vuông AC và BD, khi đó ta có SH là đường cao của hình chóp đều.
+) Áp dụng định lý Pitago cho tam giác ABC vuông tại B:
AB2 + BC2 = AC2
⇔ AC2 = 32 + 32 = 18
=> AC = √18=3√2 cm
=> HC = 12AC
= 12.3√2=3√22 cm (Vì H là trung điểm AC)
Áp dụng định lý Pitago cho tam giác SHC vuông tại H có:
SH2 + HC2 = SC2
⇔SH2 = SC2 - HC2
= 52 -(3√22)2=824=412
Vậy SH2 =412
Câu 27:
18/07/2024Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SB = 5cm.
1. Tính bình phương đường cao SH của hình chóp.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải

Lấy H là giao của 2 đường chéo hình vuông AC và BD, khi đó ta có SH là đường cao của hình chóp đều.
+) Áp dụng định lý Pitago cho tam giác ABC vuông tại B:
AB2 + BC2 = AC2
⇔ AC2 = 32 + 32 = 18
=> AC = √18=3√2 cm
=> HC = 12AC
= 12.3√2=3√22 cm (Vì H là trung điểm AC)
Áp dụng định lý Pitago cho tam giác SHC vuông tại H có:
SH2 + HC2 = SC2
⇔SH2 = SC2 - HC2
= 52 -(3√22)2=824=412
Vậy SH2 =412
Câu 28:
18/07/2024Cho hình chóp tứ giác đều S.ABCD, đáy ABCD là hình vuông có cạnh 3cm, cạnh bên SB = 5cm.
2. Tính diện tích xung quanh hình chóp
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
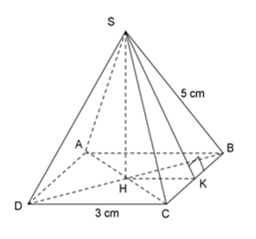
+ Kẻ SK vuông góc với BC (K BC)
+ Vì tam giác SBC là tam giác cân tại S nên SK vừa là đường cao vừa là đường trung tuyến.
=> CK = KB = 12BC = 32cm
Áp dụng định lý Pitago cho tam giác SKB vuông tại K:
SK2 + KB2 = SB2
SK2 = SB2 - KB2
= 52 - (32)2=914
=> SK = √912cm
Vậy diện tích xung quanh của hình chóp đều S.ABCD là:
Sxq = 4.SABC = 4.12BC.SK
= 4. 12.3.√912=3√91cm2
Có thể bạn quan tâm
- Trắc nghiệm ôn tập Chương 4 Hình học: Hình lăng trụ đứng. Hình chóp đều (có đáp án) (447 lượt thi)
- Tổng hợp Lý thuyết & Trắc nghiệm Chương 4 Hình học 8 (273 lượt thi)
- Trắc nghiệm Bài 10: Ôn tập chương 4 Hình học có đáp án (Nhận biết) (240 lượt thi)
- Trắc nghiệm Bài 10: Ôn tập chương 4 Hình học có đáp án (Thông hiểu) (231 lượt thi)
- Trắc nghiệm Bài 10: Ôn tập chương 4 Hình học có đáp án (Vận dụng) (248 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Thể tích hình chóp đều (có đáp án) (765 lượt thi)
- Bài tập Hình chóp đều và hình chóp cụt đều (có lời giải chi tiết) (655 lượt thi)
- Trắc nghiệm Hình lăng trụ đứng có đáp án (Nhận biết) (571 lượt thi)
- Trắc nghiệm Diện tích xung quanh hình lăng trụ (có đáp án) (496 lượt thi)
- Trắc nghiệm Hình chóp đều và hình chóp cụt đều (có đáp án) (479 lượt thi)
- Trắc nghiệm Thể tích hình lăng trụ đứng (có đáp án) (470 lượt thi)
- Trắc nghiệm Diện tích xung quanh hình chóp đều (có đáp án) (440 lượt thi)
- Trắc nghiệm Hình lăng trụ đứng có đáp án (Thông hiểu) (427 lượt thi)
- Trắc nghiệm Thể tích hình hộp chữ nhật (có đáp án) (406 lượt thi)
- Trắc nghiệm Thể tích của hình lăng trụ đứng có đáp án (Thông hiểu) (388 lượt thi)
