Lời giải. Lấy hai điểm A và $A\text{'}$ tùy ý trên d và $d\text{'}$.

Chọn điểm O thỏa mãn $\overrightarrow{OA\text{'}}=20\overrightarrow{OA}$.

Khi đó phép vị tự tâm O tỉ số $k=20$ sẽ biến d thành đường thẳng $d\text{'}$.

Do A và $A\text{'}$ tùy ý trên d và $d\text{'}$ nên suy ra có vô số phép vị tự.

Lời giải.

Vì qua phép vị tự, đường thẳng biến thành đường thẳng song song hoặc trùng với nó.

Lời giải.

Ta có  $\overrightarrow{AB}=\left(-4;2\right).$

Từ giả thiết, ta có

 $\overrightarrow{A\text{'}B\text{'}}=-\frac{1}{3}\overrightarrow{AB}=\left(\frac{4}{3};-\frac{2}{3}\right).$

Lời giải.

Tâm vị tự là giao điểm của d và $d\text{'}$. Tỉ số vị tự là số k khác 0

(hoặc tâm vị tự tùy ý, tỉ số k=1 - đây là phép đồng nhất).

Lời giải.

Theo tính chất 1, ta có $\overrightarrow{BD}=2\overrightarrow{AC}$.

Lời giải.

Do D là trung điểm BC nên AD là đường trung tuyến của tam giác ABC .

Suy ra  $\overrightarrow{GD}=-\frac{1}{2}\overrightarrow{GA}$

$\underset{}{\to }{V}_{\left(G,-\frac{1}{2}\right)}\left(A\right)=D$.

Vậy $k=-\frac{1}{2}$.

Lời giải.

Phép vị tự có tâm tùy ý, tỉ số vị tự  k= 1

Lời giải.

Phép vị tự có tâm là , tỉ số vị tự $k=\pm \frac{R\text{'}}{R}.$

Lời giải.

Ta có  

$V_{\left(O,k\right)}\left(M\right)=M^{\text{'}}\stackrel{}{\leftrightarrow }\overrightarrow{O{M}^{\text{'}}}=k\overrightarrow{OM}$

$\stackrel{}{\to }\overrightarrow{OM}=\frac{1}{k}\overrightarrow{O{M}^{\text{'}}}\left(k\ne 0\right).$

Lời giải.

Ta có $V_{\left(O,-3\right)}\left(A\right)=C\stackrel{}{\leftrightarrow }\overrightarrow{OC}=-3\overrightarrow{OA}$

 và $V_{\left(O,-3\right)}\left(B\right)=D\stackrel{}{\leftrightarrow }\overrightarrow{OD}=-3\overrightarrow{OB}.$

Khi đó  $\overrightarrow{OC}-\overrightarrow{OD}=-3\left(\overrightarrow{OA}-\overrightarrow{OB}\right)$

$\iff \overrightarrow{DC}=-3\overrightarrow{BA}\iff \overrightarrow{DC}=3\overrightarrow{AB}.$

Lời giải.

Phép vị tự có tâm là trung điểm $OO\text{'}$, tỉ số vị tự bằng -1 . 

Lời giải.

Tỉ số vị tự  $k=\pm 1.$

Lời giải

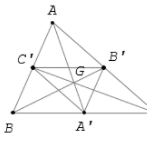
Theo giả thiết, ta có 

$\left\{\begin{array}{l}\overrightarrow{GA}=-2\overrightarrow{GA\text{'}}\\ \overrightarrow{GB}=-2\overrightarrow{GB\text{'}}\\ \overrightarrow{GC}=-2\overrightarrow{GC\text{'}}\end{array}\right.$

$\underset{}{\to }\left\{\begin{array}{l}{V}_{\left(G,-2\right)}\left(A\text{'}\right)=A\\ V_{\left(G,-2\right)}\left(B\text{'}\right)=B\\ V_{\left(G,-2\right)}\left(C\text{'}\right)=C\end{array}\right.$

Vậy $V_{\left(G,-2\right)}$ biến tam giác $A\text{'}B\text{'}C\text{'}$ thành tam giác ABC.

Lời giải.

Chọn $A\left(1;1\right)\in {\Delta }_1$.

Ta có $V_{\left(I,k\right)}\left(A\right)=B\left(x;y\right)$

$\stackrel{}{\to }\left\{\begin{array}{l}\overrightarrow{IB}=k\overrightarrow{IA}\\ B\in {\Delta }_2\end{array}\right..$

Từ $\overrightarrow{IB}=k\overrightarrow{IA}\underset{}{\to }B\left(2-k;1\right)$.

Do $B\in {\Delta }_2$ nên  $\left(2-k\right)-2.1+4=0$

$\iff k=4.$

Lời giải.

Đường tròn $\left(C\right)$ có tâm $K\left(1;5\right)$ và bán kính $R=2.$

Gọi $K\text{'}\left(x;y\right)$ là tâm của đường tròn $\left(C\text{'}\right)$.

$K\text{'}\left(x;y\right)=V_{\left(I,-2\right)}\left(K\right)$

$\iff \overrightarrow{IK\text{'}}=-2\overrightarrow{IK}$

$\iff \left\{\begin{array}{l}x-2=-2\left(1-2\right)\\ y+3=-2\left(5+3\right)\end{array}\right.$

$\iff \left\{\begin{array}{l}x=4\\ y=-19\end{array}\right.\Rightarrow K\text{'}\left(4;-19\right)$

Bán kính $R\text{'}$ của $\left(C\text{'}\right)$ là

$R\text{'}=\left|k\right|.R=2.2=4.$

Vậy $\left(C\text{'}\right):{\left(x-4\right)}^2+{\left(y+19\right)}^2=16$ .

Lời giải.

Qua phép vị tự $V_{\left(I,3\right)}$ thì 

$A\text{'}B\text{'}=3AB$

$B\text{'}C\text{'}=3BC$

$C\text{'}A\text{'}=3CA.$

Vậy chu vi tam giác $A\text{'}B\text{'}C\text{'}$ gấp 3 lần chu vi tam giác ABC .

Lời giải. Từ giả thiết suy ra hình vuông ban đầu có độ dài cạnh bằng 2.

Qua phép vị tự $V_{\left(I,-2\right)}$ thì độ dài cạnh của hình vuông tạo thành bằng 4 ,

suy ra diện tích bằng 16 .

Vậy diện tích tăng gấp 4 lần.

Lời giải.

Ta có

 $R\text{'}=\left|k\right|.R=5.R=5.3=15.$

Lời giải.

Gọi $M\text{'}\left(x;y\right)$.

Suy ra  $\overrightarrow{IM}=\left(-9;-1\right)$

$\hspace{0.17em}\overrightarrow{IM\text{'}}=\left(x-2;y-3\right).$

Ta có  $V_{\left(I,-2\right)}\left(M\right)=M\text{'}$

$\iff \overrightarrow{IM\text{'}}=-2\overrightarrow{IM}$

$\underset{}{\to }\left\{\begin{array}{l}x-2=-2.\left(-9\right)\\ y-3=-2.\left(-1\right)\end{array}\right.$

$\iff \left\{\begin{array}{l}x=20\\ y=5\end{array}\right.$

$\Rightarrow M\text{'}\left(20;5\right).$

Lời giải.

Gọi $B\text{'}\left(x;y\right)$ là ảnh của B qua phép vị tự V.

Suy ra $\overrightarrow{A\text{'}B\text{'}}=\left(x+5;y-1\right)$ và $\overrightarrow{AB}=\left(-1;3\right).$

Theo giả thiết, ta có $\overrightarrow{A\text{'}B\text{'}}=2\overrightarrow{AB}$

$\iff \left\{\begin{array}{l}x+5=2.\left(-1\right)\\ y-1=2.3\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-7\\ y=7\end{array}\right.$

Lời giải.

Kẻ đường thẳng $∆$ qua O, cắt d tại A và cắt $d\text{'}$ tại $A\text{'}$.

Gọi k là số thỏa mãn $\overrightarrow{OA\text{'}}=k\overrightarrow{OA}$.

Khi đó phép vị tự tâm O tỉ số k sẽ biến d thành đường thẳng $d\text{'}$.

Do k xác định duy nhất (không phụ thuộc vào $∆$) nên có duy nhất một phép vị tự.

Lời giải.

Gọi $I\left(x;y\right)$.

Suy ra  $\overrightarrow{IM}=\left(4-x;6-y\right),$

$\hspace{0.17em}\overrightarrow{IM\text{'}}=\left(-3-x;5-y\right).$ 

Ta có $V_{\left(I,\frac{1}{2}\right)}\left(M\right)=M\text{'}.$

$\iff \overrightarrow{IM\text{'}}=\frac{1}{2}\overrightarrow{IM}$

$\iff \left\{\begin{array}{l}-3-x=\frac{1}{2}\left(4-x\right)\\ 5-y=\frac{1}{2}\left(6-y\right)\end{array}\right.$

$\iff \left\{\begin{array}{l}x=-10\\ y=4\end{array}\right.$

$\Rightarrow I\left(-10;4\right)$

Lời giải.

Ta có $\overrightarrow{IM\text{'}}=\left(1;2\right),\overrightarrow{IM}=\left(3;6\right).$

Theo giả thiết: $V_{\left(I,k\right)}\left(M\right)=M\text{'}$

$\iff \overrightarrow{IM\text{'}}=k\overrightarrow{IA}$

$\iff \left\{\begin{array}{l}1=k.3\\ 2=k.6\end{array}\right.$

$\iff k=\frac{1}{3}.$

Lời giải.

Ta có $V_{\left(O,2\right)}:d\mapsto d^{\text{'}}\stackrel{}{\to }d\parallel d^{\text{'}}$ nên

$d\text{'}:2x+y+c=0\left(c\ne -3\right).$

Chọn $A\left(0;3\right)\in d.$

Ta có $V_{\left(O,2\right)}\left(A\right)=A^{\text{'}}\stackrel{}{\to }\left\{\begin{array}{l}\overrightarrow{O{A}^{\text{'}}}=2\overrightarrow{OA}\\ A^{\text{'}}\in d^{\text{'}}\end{array}\right..$

Từ $\overrightarrow{O{A}^{\text{'}}}=2\overrightarrow{OA}\stackrel{}{\to }{A}^{\text{'}}\left(0;6\right).$

Thay vào $d\text{'}$ ta được $d\text{'}:2x+y-6=0.$

Cách 2.

Giả sử phép vị tự $V_{\left(O,2\right)}$ biến điểm $M\left(x;y\right)$ thành điểm $M\text{'}\left(x\text{'};y\text{'}\right).$

Ta có $\overrightarrow{OM\text{'}}=2\overrightarrow{OM}$

$\iff \left\{\begin{array}{l}x\text{'}=2x\\ y\text{'}=2y\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}x=\frac{x\text{'}}{2}\\ y=\frac{y\text{'}}{2}\end{array}\right.$.

Thay vào d ta được $2.\frac{x\text{'}}{2}+\frac{y\text{'}}{2}-3=0$

$\iff 2x\text{'}+y\text{'}-6=0.$  

Lời giải.

Nhận xét. Mới đọc bài toán nghĩ rằng đề cho thiếu dữ kiện,

cụ thể không cho k bằng bao nhiêu thì sao tìm được $∆\text{'}$.

Để ý thấy $I\in \Delta$ do đó phép vị tự tâm I tỉ số k biến đường thẳng $∆$ thành $∆\text{'}$ trùng với $∆$,

với mọi $k\ne 0.$  

Lời giải.

Do ABCD là hình thang có $AB\parallel CD$ và $AB=3CD$

Suy ra $\overrightarrow{AB}=3\overrightarrow{DC}.$

Giả sử có phép vị tự tâm O, tỉ số k thỏa mãn bài toán.

- Phép vị tự tâm O , tỉ số k biến điểm $A\stackrel{}{\to }C$

Suy ra  $\overrightarrow{OC}=k\overrightarrow{OA}\left(1\right).$

- Phép vị tự tâm O , tỉ số k biến điểm $B\stackrel{}{\to }D$

Suy ra $\overrightarrow{OD}=k\overrightarrow{OB}\left(2\right).$

Từ $\left(1\right)$ và $\left(2\right)$, suy ra $\overrightarrow{OC}-\overrightarrow{OD}=k\left(\overrightarrow{OA}-\overrightarrow{OB}\right)$

$\iff \overrightarrow{DC}=k\overrightarrow{BA}$

$\iff \overrightarrow{AB}=-\frac{1}{k}\overrightarrow{DC}.$

Mà $\overrightarrow{AB}=3\overrightarrow{DC}$  

suy ra $-\frac{1}{k}=3$

$\iff k=-\frac{1}{3}$.

Nhận xét. Tâm vị tự là giao điểm của hai đường chéo trong hình thang. Bạn đọc cũng có thể chứng minh bằng hai tam giác đồng dạng.

Lời giải.

Từ giả thiết,

suy ra $\left\{\begin{array}{l}{V}_{\left(I,k\right)}\left(A\right)=C\\ V_{\left(I,k\right)}\left(B\right)=D\end{array}\right.$

$\iff \left\{\begin{array}{l}\overrightarrow{IC}=k\overrightarrow{IA}\\ \overrightarrow{ID}=k\overrightarrow{IB}\end{array}\right.$.

Suy ra $\overrightarrow{ID}-\overrightarrow{IC}=k\left(\overrightarrow{IB}-\overrightarrow{IA}\right)$

$\iff \overrightarrow{CD}=k\overrightarrow{AB}.$

 Kết hợp giả thiết suy ra $k=-\frac{1}{2}.$