Lời giải.

Tam giác đều có 3 trục đối xứng (đường thẳng đi qua đỉnh tam giác và trung điểm cạnh đối diện).

Lời giải. Tọa độ giao điểm A của d và $∆$ thỏa mãn hệ $\left\{\begin{array}{l}3x+y-1=0\\ 2x-y+1=0\end{array}\right.\Rightarrow A\left(0;1\right).$

Vì $A\in \Delta$ nên qua phép đối xứng trục $∆$ biến thành chính nó, tức $A\text{'}\equiv A\left(0;1\right).$

Chọn điểm $B\left(1;-2\right)\in d$.

Đường thẳng đi qua điểm B và vuông góc với $∆$ có phương trình $\mathcal{l}:x+2y+3=0$.

Gọi $H=\Delta \cap \mathcal{l}$, suy ra tọa độ điểm H thỏa hệ $\left\{\begin{array}{l}2x-y+1=0\\ x+2y+3=0\end{array}\right.\Rightarrow H\left(-1;-1\right).$

Gọi $B\text{'}\left(x\text{'};y\text{'}\right)$ là điểm đối xứng của B qua $\Delta$$\to H$ là trung điểm của $BB\text{'}$

$\iff \left\{\begin{array}{l}x\text{'}=2x_H-x_B\\ y\text{'}=2y_H-y_B\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}x\text{'}=-3\\ y\text{'}=0\end{array}\right.$

$\Rightarrow B\text{'}\left(-3;0\right).$

Đường thẳng $d\text{'}$ cần tìm đi qua hai điểm $A\text{'},B\text{'}$ nên có phương trình $x-3y+3=0.$

Lời giải. Biểu thức tọa độ của phép đối xứng qua trục $d:y-x=0$ (đường phân giác góc phần tư thứ nhất) là $\left\{\begin{array}{c}x\text{'}=y\\ y\text{'}=x\end{array}\right.$.

Thay vào $\left(C\right)$, ta được ${\left(y\text{'}+1\right)}^2+{\left(x\text{'}-4\right)}^2=1$ hay  ${\left(x-4\right)}^2+{\left(y+1\right)}^2=1.$

Lời giải.

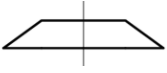
Hình thang cân có trục đối xứng (đường thẳng đi qua trung điểm của hai cạnh đáy).

Lời giải.

Đoạn thẳng có 1 trục đối xứng là đường trung trực của đoạn thẳng.

Đường tròn có vô số trục đối xứng là các đường thẳng đi qua tâm.

Tam giác đều có 3 trục đối xứng là các đường thẳng đi qua đỉnh và trung điểm cạnh đối diện.

Hình vuông có 4 trục đối xứng.

Vậy hình tròn có nhiều trục đối xứng nhất.

Lời giải.

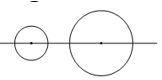
Có duy nhất một trục đối xứng đi qua tâm của hai đường tròn.

Lời giải.

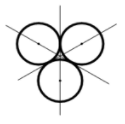
Có 3 trục đối xứng như hình vẽ.

Lời giải.

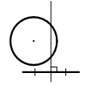
Trường hợp trục đối xứng của đoạn thẳng không đi qua tâm của đường tròn như hình vẽ.

Lời giải.

Gọi $∆$ là đường thẳng vuông góc với đường thẳng d 

Khi đó, phép đối xứng trục $∆$ biến d thành chính nó.

Có vô số đường thẳng $∆$ vuông góc với d

Lời giải.

Hai đường thẳng cắt nhau tạo ra 4 góc

(2 cặp góc đối đỉnh bằng nhau).

Đường phân giác của 2 cặp góc đối đỉnh chính là 2 trục đối xứng biến d thành $d\text{'}$ .

Lời giải.

Qua trục đối xứng là đường thẳng a sẽ biến a thành a và biến b thành b .

Qua trục đối xứng là đường thẳng b sẽ biến a thành a và biến b thành b .

Lời giải.

Đây là trường hợp đặc biệt của Câu 11 và Câu 12.

Có 2 trục đối xứng là 2 đường phân giác của 2 cặp góc tạo bởi d và $d\text{'}$. Trường hợp này trục đối xứng biến d thành $d\text{'}$ và $d\text{'}$ thành d

Có 2 trục đối xứng chính là d và $d\text{'}$. Trường hợp này trục đối xứng biến d thành chính nó và $d\text{'}$ thành chính nó.

Lời giải.

Để biến a thành a thì trục đối xứng trùng với a hoặc vuông góc với a.

TH1: Trục đối xứng trùng với a , mà a tạo với b góc  ${60}^0$$\stackrel{}{\to }a$ không là trục đối xứng để biến b thành b .

TH2: Trục đối xứng vuông góc với a , mà a tạo với b góc ${60}^0\stackrel{}{\to }$ đường thẳng đó không là trục đối xứng để biến b thành b

Lời giải.

Đường thẳng $∆$ vuông góc với d và $d\text{'}$ sẽ biến d và $d\text{'}$ thành chính nó.

Có vô số đường thẳng $∆$ vuông góc với d và $d\text{'}$.

Lời giải.

Biểu thức tọa độ qua phép đối xứng trục tung là $\left\{\begin{array}{l}x=-x\text{'}\\ y=y\text{'}\end{array}\right..$ 

Thay vào $\left(P\right)$, ta được  $y{\text{'}}^2=-x\text{'}.$

Lời giải.

Biểu thức tọa độ qua phép đối xứng trục $Ox$ là $\left\{\begin{array}{l}x=x\text{'}\\ y=-y\text{'}\end{array}\right..$ 

Thay vào $\left(P\right)$, ta được $-y\text{'}=x{\text{'}}^2-2x\text{'}+3$ hay  $y\text{'}=-x{\text{'}}^2+2x\text{'}-3.$

Lời giải.

Để biến đường thẳng c thành chính nó thì trục đối xứng có dạng trùng với c hoặc vuông góc với  c

TH1: Trục đối xứng trùng với $c\stackrel{}{\to }$ trục đối xứng vuông góc với a và  b $\Rightarrow$trục đối xứng biến a và b thành chính nó. Do đó trường hợp này không thỏa mãn.

TH2: Trục đối xứng vuông góc với c , tức là trục đối xứng song song (hoặc trùng) với a và b. Khi đó, để trục đối xứng biến a thành b thì trục đối xứng phải cách đều a và b. Do đó trường hợp này có 1 trục đối xứng thỏa mãn.

Lời giải.

Hàm số $y=\cos x$ là hàm số chẵn nên đồ thị nhận đường thẳng $x=0$ (trục tung) làm trục đối xứng.

Lại có các đường thẳng cách trục tung một đoạn bằng một số nguyên lần $\mathrm{\pi }$ cũng là trục đối xứng của đồ thị.

Lời giải.

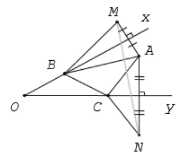
Gọi M là điểm đối xứng với A qua Ox. Vì $B\in Ox$ nên suy ra $BA=BM.$ 

Gọi N là điểm đối xứng với A qua Oy  Vì $C\in Oy$ nên suy ra $CA=CN.$

Chu vi tam giác:

 $P_{\Delta ABC}$= AB+BC+CA = BM+BC+CN $\left(*\right)$   

Theo bất đẳng thức tam giác mở rộng, ta có $MB+BC\ge MC$ và $MC+CN\ge MN.$

Kết hợp với $\left(\ast \right)$, suy ra :

$P_{\Delta ABC}$= (MB + BC) + CN 

$\ge$MC + CN $\ge$ MN

Dấu $"="$ xảy ra khi và chỉ khi B,C,M,N thẳng hàng hay C là giao điểm của BM với trục Oy.

Lời giải.

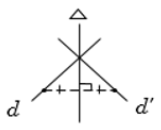
Trường hợp đường thẳng không song song hoặc không trùng với trục đối xứng thì ảnh của nó sẽ cắt đường thẳng đã cho (Hình vẽ).

Lời giải.

Biểu thức tọa độ qua phép đối xứng trục $Ox$:

Gọi M’(x’; y’) = Đ_Ox[M(x; y)] thì M’ có tọa độ  $\left\{\begin{array}{l}x\text{'}=x\\ y\text{'}=-y\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=2\\ y\text{'}=-3\end{array}\right..$

Do đó M’(2; -3).

Lời giải.

Biểu thức tọa độ qua phép đối xứng trục Oy:

Gọi A’(x’; y’) = Đ_Oy[A(x; y)] thì A’ có tọa độ $\left\{\begin{array}{l}x\text{'}=-x\\ y\text{'}=y\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=-3\\ y\text{'}=5\end{array}\right..$

Lời giải.

Tọa độ trọng tâm: $\left\{\begin{array}{l}{x}_G=\frac{x_A+x_B+x_C}{3}\\ y_G=\frac{y_A+y_B+y_C}{3}\end{array}\right.$

$\Rightarrow \left\{\begin{array}{l}{x}_G=2\\ y_G=1\end{array}\right.\Rightarrow G\left(2;1\right).$

Gọi $G\text{'}\left(x\text{'};y\text{'}\right)=$${Ñ}_{Oy}\left[G\left(x;y\right)\right]$ thì  $\left\{\begin{array}{l}x\text{'}=-x\\ y\text{'}=y\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=-2\\ y\text{'}=1\end{array}\right..$

Lời giải.

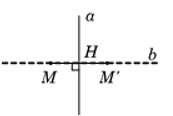
Đường thẳng b qua M và vuông góc với a có phương trình $b:y+3=0.$

Gọi $H=a\cap b,$ tọa độ điểm H là nghiệm của hệ $\left\{\begin{array}{l}x+2=0\\ y+3=0\end{array}\right.\Rightarrow H\left(-2;-3\right).$

Theo giả thiết: ${Đ}_a\left(M\right)=M\text{'}\left(x\text{'};y\text{'}\right)\to H$ là trung điểm của $MM\text{'}$

$\left\{\begin{array}{l}x\text{'}=2x_H-x_M\\ y\text{'}=2y_H-y_M\end{array}\right.\Rightarrow \left\{\begin{array}{l}x\text{'}=-8\\ y\text{'}=-3\end{array}\right.$

$\stackrel{}{\to }M\text{'}\left(-8;-3\right).$

Lời giải.

Nhận xét: đường thẳng $d:x-y=0\iff d:y=x$ là đường phân giác của góc phần tư thứ nhất.

Biểu thức tọa độ qua phép đối xứng đường phân giác $y=x$ là:

Gọi $M\text{'}\left(x\text{'};y\text{'}\right)=$ Đ_d[M(x; y)] thì  $\left\{\begin{array}{l}x\text{'}=y\\ y\text{'}=x\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=3\\ y\text{'}=2\end{array}\right..$

Lời giải.

Đường thẳng d qua A và vuông góc với $∆$ có phương trình $d:x+2y-7=0$

Gọi $H=d\cap \Delta ,$ tọa độ điểm H là nghiệm của hệ $\left\{\begin{array}{l}2x-y+1=0\\ x+2y-7=0\end{array}\right.$

$\iff \left\{\begin{array}{l}x=1\\ y=3\end{array}\right.\Rightarrow H\left(1;3\right).$

Theo giả thiết: ${Đ}_{\Delta }\left(A\right)=A\text{'}\left(x\text{'};y\text{'}\right)$

$\to H$ là trung điểm của $AA\text{'}$

$\iff \left\{\begin{array}{l}x\text{'}=2x_H-x_A\\ y\text{'}=2y_H-y_A\end{array}\right.\Rightarrow \left\{\begin{array}{l}x\text{'}=-1\\ y\text{'}=4\end{array}\right.$

$\stackrel{}{\to }A\text{'}\left(-1;4\right).$

Lời giải.

Đường phân giác của góc phần tư thứ hai có phương trình $d:y=-x.$

Biểu thức tọa độ qua phép đối xứng đường phân giác $d:y=-x$ là:

Gọi $P\text{'}\left(x\text{'};y\text{'}\right)=$Đ_d[P(x; y)] thì  $\left\{\begin{array}{l}x\text{'}=-y\\ y\text{'}=-x\end{array}\right.\iff \left\{\begin{array}{l}x\text{'}=2\\ y\text{'}=-5\end{array}\right..$