Trắc nghiệm Ôn tập Toán 12 Chương 2: Hình học (có đáp án)
Trắc nghiệm Toán 12 Bài: Ôn tập Chương 2 Hình học
-
345 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Khi quay đường thẳng, đường tròn quanh một trục cố định thì ta được mặt tròn xoay.
Khi quay một điểm quanh trục cố định ta chỉ được một đường tròn.
Câu 2:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đáp án A: quay elip quanh trục đối xứng của nó ta được mặt tròn xoay nhưng không phải mặt cầu
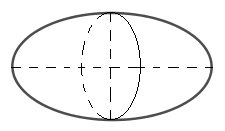
Đáp án B: quay parabol quanh trục đối xứng của nó ta được mặt tròn xoay mà không phải mặt cầu.
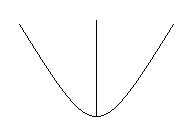
Đáp án C: quay đường tròn quanh đường kính của nó ta được mặt cầu.
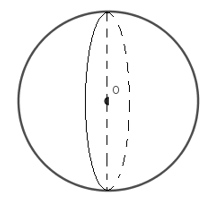
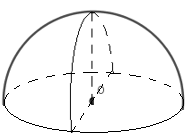
Đáp án D: quay nửa đường tròn quanh trục đối xứng của nó ta chỉ được nửa mặt cầu
Câu 3:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Nếu OH < R thì (P) cắt (S) theo giao tuyến là một đường tròn
Câu 4:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Mặt cầu (S) và đường thẳng d không có điểm chung nếu d(O;d)>R
Câu 5:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
là góc giữa hai đường thẳng d, d’ thì góc là góc ở đỉnh của mặt nón.
Câu 6:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Quay hình tam giác vuông ABC tại A có quanh trục là đường thẳng AC ta được hình nón đỉnh C có góc ở đỉnh
Câu 7:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Điểm không thuộc mặt cầu thì có thể nằm ngoài hoặc nằm trong mặt cầu nên các điểm nằm trong mặt cầu vẫn thuộc khối cầu.
Do đó C sai.
Câu 8:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Nếu (P) là mặt phẳng kính thì OH = 0 (H trùng O) hay (P) đi qua O là tâm mặt cầu, do đó (P) đi qua đường kính của mặt cầu.
Câu 9:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Hình chóp có cạnh bên vuông góc với đáy nội tiếp mặt cầu có bán kính với r là bán kính đường tròn đáy, h là chiều cao hình chóp (độ dài cạnh bên vuông góc với đáy)
Câu 10:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Đường kính mặt cầu ngoại tiếp hình lập phương cạnh a là
Câu 11:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Trục đa giác đáy: là đường thẳng đi qua tâm đường tròn ngoại tiếp đa giác đáy và vuông góc với mặt phẳng chứa đa giác đáy.
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Mọi điểm nằm trên mặt phẳng trung trực của đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng và ngược lại
Câu 13:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Áp dụng công thức : ta được:
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Vì góc ở đỉnh bằng nên thiết diện qua trục là tam giác đều cạnh , do đó độ dài đường sinh:
Diện tích đáy:
Diện tích toàn phần:
Câu 15:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Công thức tính diện tích mặt cầu:
Câu 16:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
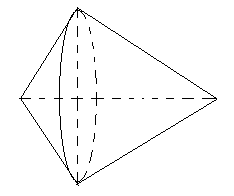
Quay tam giác vuông ABC quanh cạnh huyền BC ta được hai hình nón.
Câu 17:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Hình nón có bán kính đáy R và chiều cao h thì đường sinh
Khi đó diện tích xung quanh hình nón là:
Câu 18:
20/07/2024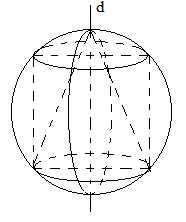
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Quan sát hình vẽ ta thấy hình trụ nội tiếp mặt cầu, hình nón nội tiếp mặt cầu, mặt cầu ngoại tiếp hình nón nên các đáp án A, C và D đúng.
Ngoài ra hình nón không nội tiếp hình trụ vì hình trụ không đi qua đỉnh hình nón.
Câu 19:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
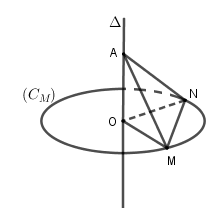
Đường tròn là đường tròn đi qua điểm M
Vì nhưng MN chưa chắc là đường kính nên A sai.
Ngoài ra,
vuông góc với mp chứa nên vuông góc với mọi đường thẳng thuộc mp này.
Do đó
Tam giác vuông AOM = AON (hai cạnh góc vuông) nên AM = AN.
Vậy các đáp án còn lại đều đúng.
Câu 20:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
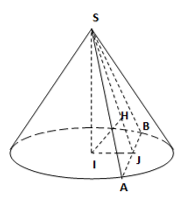
Gọi J là trung điểm của AB.
Có:
Nên:
Nên:
Và
Vậy
Câu 21:
15/07/2024Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
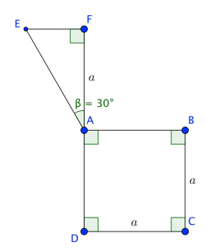
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có:
Khi quay quanh trục DF, tam giác AEF tạo ra một hình nón có thể tích
Khi quay quanh trục DF, hình vuồn ABCD tạo ra một hình trụ có thể tích
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF là:
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
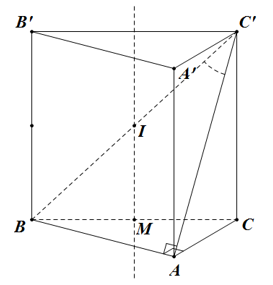
Gọi M là trung điểm BC, I là trung điểm BC’.
Khi đó, IM là trục của đường tròn ngoại tiếp tam giác ABC.
Mặt khác, . Do dó, I là tâm mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’
Bán kính
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
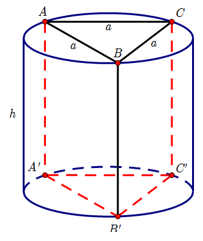
Khối trụ ngoại tiếp lăng trụ tam giác đều có hình tròn đáy là hình nón ngoại tiếp tam giác đáy của lăng trụ, và chiều cao bằng chiều cao lăng trụ.
Tam giác đều cạnh a có bán kính đương tròn ngoại tiếp bằng: .
Vậy thể tích của khối trụ cần tìm:
(đvtt)
Câu 24:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
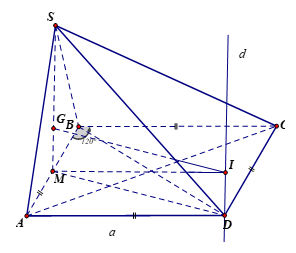
Do
đều.
nên D là tâm đường tròn ngoại tiếp
Gọi M là trung điểm của AB, G là trọng tâm của tam giác SAB.
Qua D kẻ và qua G kẻ
Gọi
Ta có:
Khi đó I là tâm của mặt cầu ngoại tiếp hình chóp S.ABC có bán kính
Câu 25:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Dựa vào giả thiết ta có bán kính đáy hình nón là bán kính đường tròn nội tiếp hình vuông nên
Chiều cao hình nón là khoảng cách từ O đến mp (ABCD) nên h = 2a.
Độ dài đường sinh hình nón là:
Diện tích xung quanh của hình nón là:
Câu 26:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
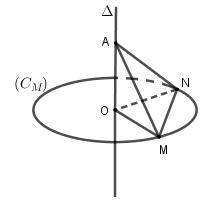
Đường tròn là đường tròn đi qua điểm M
Vì nhưng MN chưa chắc là đường kính nên E sai.
Ngoài ra,
vuông góc với mp chứa nên vuông góc với mọi đường thẳng thuộc mp này.
Do đó
Tam giác vuông AOM = AON (hai cạnh góc vuông) nên AM = AN.
Vậy các đáp án còn lại đều đúng.
Câu 27:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
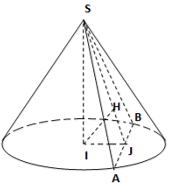
Gọi J là trung điểm của AB.
Có:
Nên:
Nên:
Và
Vậy
Câu 28:
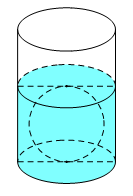
22/07/2024Người ta thả một viên billiards có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4 cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5 cm. Bán kính của viên billiards đó bằng:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Thể tích mực nước ban đầu là:
Gọi R là bán kính của viên bi ta có sau khi thả viên bi vào cốc, chiều cao của mực nước bằng 2R, do đó tổng thể tích của nước và bi sau khi thẻ viên bi vào trong cốc là:
Thể tích của quả cầu là:
Ta có:
Giải phương trình trên với điều kiện
Câu 29:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
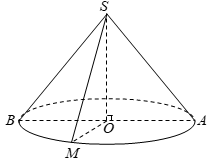
Giả sử O là tâm đáy và AB là một đường kính của đường tròn đáy hình nón.
Thiết diện qua đỉnh của hình nón là tam giác can SAM. Theo giả thiết hình nón có bán kính đáy
nên
Xét tam giác SOA vuông tại O, ta có
Diện tích thiết diện là
Do nên lớn nhất khi và chỉ khi hay khi tam giác ASM vuông cân đỉnh S (vì nên tồn tại tam giác ASM thỏa mãn)
Vậy diện tích thiết diện lớn nhất là: (đvdt)
Câu 30:
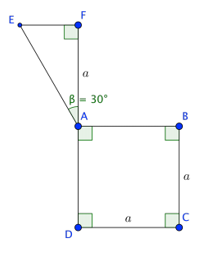
21/07/2024Tính thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có:
Khi quay quanh trục DF, tam giác AEF tạo ra một hình nón có thể tích
Khi quay quanh trục DF, hình vuồn ABCD tạo ra một hình trụ có thể tích
Thể tích của vật thể tròn xoay khi quay mô hình (như hình vẽ) quanh trục DF là:
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập Toán 12 Chương 2: Hình học (có đáp án) (344 lượt thi)
- 20 câu trắc nghiệm: Ôn tập chương 2 Hình học 12 có đáp án (328 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (Nhận biết) (343 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (Thông hiểu) (312 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (Vận dụng) (0 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (382 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Thông hiểu) (699 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay (có đáp án) (549 lượt thi)
- Trắc nghiệm Mặt cầu (có đáp án) (465 lượt thi)
- 52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án (454 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Thông hiểu) (390 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Vận dụng) (386 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Nhận biết) (368 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Vận dụng) (368 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Thông hiểu) (350 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Nhận biết) (342 lượt thi)
