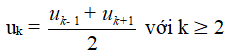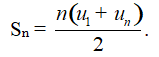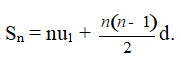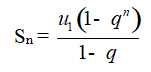Trắc nghiệm Ôn tập chương III-Dãy số, cấp số cộng, cấp số nhân (có đáp án )
Trắc nghiệm Ôn tập chương III-Dãy số, cấp số cộng, cấp số nhân (có đáp án )
-
334 lượt thi
-
37 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho dãy số (un) với un=1n2+n.Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Ta có : un+1−un=1(n+1)2+(n+1)−1n2+n
=1(n+1)(n+2)−1n(n+1)= n−(n+2)n(n+1)(n+2)=−2n(n+1)(n+2)<0
Do đó (un) là dãy giảm.
Chọn đáp án B.
Câu 2:
19/07/2024Cho dãy số có các số hạng đầu là:0;12;23;34;45;....Số hạng tổng quát của dãy số này là:
 Xem đáp án
Xem đáp án
Ta có:
0=00+1;12=11+1;23=22+134=33+1;45=44+1
Suy ra un=nn+1
Chọn đáp án B
Câu 3:
21/07/2024Xét tính tăng giảm của các dãy số sau: un=3n2−2n+1n+1
 Xem đáp án
Xem đáp án
Ta có:
un+1−un= 3(n+1)2−2(n+1)+1n+2− 3n2−2n+1n+1= 3n2+4n+2n+2− 3n2−2n+1n+1= (3n2+4n+2).(n+1)−(3n2−2n+1).(n+2)(n+2).(n+1)=3n2+7n(n+1)(n+2)>0
nên dãy (un) là dãy tăng
Chọn đáp án A
Câu 4:
22/07/2024Cho cấp số cộng (un) có: u1=−0,1; d=0,1. Số hạng thứ 7 của cấp số cộng này là:
 Xem đáp án
Xem đáp án
Số hạng tổng quát của cấp số cộng (un) là:
un=u1+(n−1).0,1⇒u7=−0,1+(7−1).0,1=0,5
Chọn đáp án C.
Câu 5:
19/07/2024Cho cấp số cộng (un) thỏa mãn : {u2−u3+u5=10u4+u6=26
Xác định công sai d
 Xem đáp án
Xem đáp án
Gọi d là công sai của cấp số cộng, ta có:
{u2−u3+u5=10u4+u6=26⇔{(u1+d)−(u1+2d)+(u1+4d)=10(u1+3d)+(u1+5d)=26⇔{u1+3d=102u1+8d=26⇔{u1=1d=3
Ta có công sai d=3.
Chọn đáp án C
Câu 6:
21/07/2024Cho hai số -3 và 23. Xen kẽ giữa hai số đã cho n số hạng để tất cả các số đó tạo thành cấp số cộng có công sai d=2. Tìm n?
 Xem đáp án
Xem đáp án
Theo giả thiết thì ta được một cấp số cộng có n+2 số hạng với u1=−3, un+2=23.
Khi đó un+2=u1+(n+1)d⇔n+1=un+2−u1d=23−(−3)2=13⇔n=12
Chọn đáp án A.
Câu 7:
19/07/2024Nếu các số 5+ m; 7+2m; 17+ m theo thứ tự lập thành cấp số cộng thì m bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Ba số 5+m; 7+2m; 17+m theo thứ tự u1, u2, u3 lập thành cấp số cộng nên
u1+u3=2u2⇔(5+m)+(17+m)=2(7+2m)⇔2m+ 22= 14 + 4m ⇔−2m =− 8 ⇔m=4
Chọn đáp án C.
Câu 8:
20/07/2024Cho cấp số cộng (un) có các số hạng đầu lần lượt là 5; 9; 13; 17;..... Tìm số hạng tổng quát un của cấp số cộng.
 Xem đáp án
Xem đáp án
Các số 5; 9; 13; 17..... theo thứ tự đó lập thành cấp số cộng (un) nên
{u1=5d=u2−u1=4CTTQ→un=u1+(n−1)d=5+4(n−1)=4n+1
Chọn đáp án C.
Câu 9:
21/07/2024Cho cấp số cộng (un) có d= -2 và S8 = 72. Tìm số hạng đầu tiên u1?
 Xem đáp án
Xem đáp án
Ta có:
S8= n2.[2.u1 +(n−1)d]⇔ 72= 82. [2.u1+ (8−1).(−2)]⇔72= 4.(2u1−14) ⇔2u1−14= 18⇔2u1=32 ⇔u1=16
Chọn đáp án A
Câu 10:
19/07/2024Một cấp số cộng có 12 số hạng. Biết rằng tổng của 12 số hạng đó bằng 144 và số hạng thứ mười hai bằng 23. Khi đó công sai d của cấp số cộng đã cho là bao nhiêu?
 Xem đáp án
Xem đáp án
{u12=23S12=144 ⇒{u1+11d=23122(u1+u12)=144 ⇔{u1+11d=23u1+23=24⇔{u1=1d=23−u111=2
Chọn đáp án A
Câu 11:
19/07/2024Cho cấp số cộng (un) thỏa mãn u2 + u23 = 60. Tính tổng S24 của 24 số hạng đầu tiên của cấp số cộng đã cho.
 Xem đáp án
Xem đáp án
Ta có: u2+u23=60⇔(u1+d)+(u1+22d)=60⇔2u1+23d=60.
Khi đó S24=n2. [2u1+(n−1)d]= 242(2u1+23d)=12.60=720.
Chọn đáp án C
Câu 12:
20/07/2024Cho cấp số cộng (un) thỏa mãn {u1+u7=26u22+u62=466. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Ta có:
{u1+u7=26u22+u62=466⇔{u1+u1+6d=26(u1+d)2+(u1+5d)2=466⇔{u1=13−3d (1)(u1+d)2+(u1+5d)2=466 (2).
Thay (1) và (2) ta được:
(13−2d)2+(13+2d)2=466⇔8d2+338=466⇔8d2= 128 ⇔d2= 16⇔[d=4⇒u1=1d=−4⇒u1=25
Chọn đáp án A
Câu 13:
19/07/2024Trong các dãy số (un) sau, dãy nào là cấp số nhân?
 Xem đáp án
Xem đáp án
Kiểm tra đáp án
A. un+1un= (n+1)2+3(n+1)+3n2+n+1=n2+5n+7n2+n+1,∀n∈ℕ* , không phải là hằng số.
Vậy ( un) không phải là cấp số nhân .
B. un+1un=(n+3).3n+1(n+2).3n=3(n+3)n+2,∀n∈ℕ* , không phải là hằng số.
Vậy ( un) không phải là cấp số nhân .
C. Từ công thức truy hồi của dãy số, suy ra u1=2;u2=3;u3=2;u4=3;...
Vì u3u2≠u2u1nên ( un) không phải là cấp số nhân .
D. un+1un=(−4)2(n+1)+1(−4)2n+1= (−4)2n+2+1(−4)2n+1 =(−4)2=16,∀n∈ℕ* .
Vậy ( un) là một cấp số nhân.
Chọn đáp án D
Câu 14:
22/07/2024Cho cấp số nhân (un) với công bội q < 0 và u2=4,u4=9 . Tìm u1
 Xem đáp án
Xem đáp án
Vì q<0,u2>0 nên u3<0 .
Do đó u3=−√u2.u4=−√4.9=−6
Ta có: u22=u1.u3⇒u1=u22u3=42−6=−83 .
Chọn đáp án A
Câu 15:
19/07/2024Cho cấp số nhân (un) biết u1+u5=51;u2+u6=102 . Hỏi số 12288 là số hạng thứ mấy của cấp số nhân (un) ?
 Xem đáp án
Xem đáp án
Gọi q là công bội của cấp số nhân đã cho. Theo đề bài, ta có
{u1+u5=51u2+u6=102⇔{u1+u1.q4=51u1.q+u1.q5=102⇔{u1(1+q4)=51 (1)u1q(1+q4)=102 (2)
Lấy (2) chia (1) ta được
q=2⇒u1=3⇒un=3.2n−1
Mặt khác un=12288⇔3.2n−1=12288⇔2n−1=212⇔n=13
Chọn đáp án D
Câu 16:
19/07/2024Tìm x biết 1,x2,6−x2 lập thành cấp số nhân.
 Xem đáp án
Xem đáp án
Ta có: 1,x2,6−x2 lập thành cấp số nhân khi và chỉ khi:
(x2)2=1.(6−x2) ⇔x4=6−x2⇔x4+x−2 6=0 ⇔x2= 2⇔x=±√2
Chọn đáp án B.
Câu 17:
19/07/2024Tính tổng tất cả các số hạng của một cấp số nhân , biết số hạng đầu bằng 18, số hạng thứ hai bằng 54 và số hạng cuối bằng 39366.
 Xem đáp án
Xem đáp án
u1=18,u2=54⇒q= u2u1=3.
Lại có un=39366⇔u1.qn−1=39366⇔18.3n−1=39366⇔3n−1=37⇔n=8
Vậy S8=18.1−381−3=59040
Chọn đáp án B.
Câu 18:
08/11/2024Các số x+ 6y ; 5x + 2y; 8x + y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số x- 1 ; y + 2 ; x – 3y theo thứ tự đó lập thành một cấp số nhân. Tính x2 + y2
 Xem đáp án
Xem đáp án
Đáp án đúng: A.
*Lời giải:
Theo giả thiết ta có {(x+6y)+(8x+y)=2(5x+2y)(x−1)(x−3y)=(y+2)2
⇔{x=3y(3y−1)(3y−3y)=(y+2)2⇔{x=3y0=(y+2)2⇔{x=−6y=−2.
Suy ra x2+y2=40.
*Phương pháp giải:
- Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:
un = u1 + (n – 1 )d với n ≥ 2
- Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:
un+1 = unq với n ∈ N*
* Các lý thuyết thêm và các dạng toán về dãy số, cấp số cộng, cấp số nhân:
CẤP SỐ CỘNG
ĐỊNH NGHĨA
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d.
Số d được gọi là công sai của cấp số cộng.
Nếu (un) là cấp số cộng với công sai d, ta có công thức truy hồi
un+1 = un + d với n ∈ N*
Đặc biệt khi d = 0 thì cấp số cộng là một dãy số không đỗi (tất cả các số hạng đều bằng nhau).
SỐ HẠNG TỔNG QUÁT
Định lí 1
Nếu cấp số cộng (un) có số hạng đầu u1 và công sai d thì số hạng tổng quát un được xác định bởi công thức:
un = u1 + (n – 1 )d với n ≥ 2
TÍNH CHẤT CÁC SỐ HẠNG CỦA CẤP SỐ CỘNG
Định lí 2
Trong một cấp số cộng, mỗi số hạng (trừ số hạng đầu và cuối) đều là trung bình cộng của hai số hạng đứng kề với nó, nghĩa là
TỔNG n SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ CỘNG
Định lí 3
Cho cấp số cộng (un). Đặt Sn = u1 + u2 + u3 +…+un. Khi đó
Chú ý: Vì un = u1 + (n – 1)d nên công thức trên có thể viết lại là
CẤP SỐ NHÂN
ĐỊNH NGHĨA
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Nếu (un) là cấp số nhân với công bội q, ta có công thức truy hồi:
un+1 = unq với n ∈ N*
Đặc biệt:
+ Khi q = 0, cấp số nhân có dạng u1, 0, 0,…, 0,…
+ Khi q = 1, cấp số nhân có dạng u1, u1, u1,…, u1,…
+ Khi u1 = 0 thì với mọi q, cấp số nhân có dạng 0, 0, 0,…, 0…
SỐ HẠNG TỔNG QUÁT
Định lí 1
Nếu cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát un được xác định bởi công thức
un = u1.qn – 1 với n ≥ 2
TÍNH CHẤT CÁC SỐ HẠNG CỦA CẤP SỐ NHÂN
Định lí 2
Trong một cấp số nhân, bình phương của mỗi số hạng (trừ số hạng đầu và cuối) đều là tích của hai số hạng đứng kề với nó, nghĩa là
uk2 = uk - 1.uk + 1 với k ≥ 2
TỔNG n SỐ HẠNG ĐẦU TIÊN CỦA MỘT CẤP SỐ NHÂN
Định lí 3
Cho cấp số nhân (un) với công bội q ≠ 1. Đặt Sn = u1 + u2 + … + un. Khi đó
Chú ý: Nếu q = 1 thì cấp số nhân là u1, u1, u1,…, u1,… khi đó Sn = nu1.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Toán 11 Chương 2 (Cánh diều): Dãy số. Cấp số cộng. Cấp số nhân
Câu 19:
21/07/2024Cho dãy số (un) có un=−n2+n+1. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có :
un+1−un=[−(n+1)2+n+1+1]−[−n2+n+1]=−n2−2n−1+n+2+n2−n−1=−2n<0 ∀n≥1
Do đó (un) là một dãy giảm.
Chọn đáp án D
Câu 20:
19/07/2024Cho dãy số (un) với un=an2n+1 (a: hằng số).un+1 là số hạng nào sau đây?
 Xem đáp án
Xem đáp án
Ta có un+1=a.(n+1)2(n+1)+1=a(n+1)2n+2.
Chọn đáp án A
Câu 21:
19/07/2024Cho dãy số có các số hạng đầu là:8,15,22,29,36,....Số hạng tổng quát của dãy số này là:
 Xem đáp án
Xem đáp án
Ta có:
8 = 7.1 + 1
15 = 7.2 + 1
22 = 7.3 + 1
29 = 7.4 + 1
36 = 7.5 + 1
Suy ra số hạng tổng quát un=7n+1.
Chọn đáp án C.
Câu 22:
19/07/2024Xét tính tăng, giảm và bị chặn của dãy số (un), biết: un=2n−133n−2
 Xem đáp án
Xem đáp án
Ta có: un+1−un=2n−113n+1−2n−133n−2=35(3n+1)(3n−2)>0 với mọi n≥1
Suy ra un+1>un ∀n≥1⇒ dãy (un) là dãy tăng.
Mặt khác: un=23−353(3n−2)⇒−11≤un<23 ∀n≥1
Vậy dãy (un) là dãy bị chặn.
Chọn đáp án A
Câu 23:
19/07/2024Xét tính tăng, giảm và bị chặn của dãy số (un), biết: un=1√1+n+n2
 Xem đáp án
Xem đáp án
Ta có: un>0 ∀n≥1
un+1un=√n2+n+1√(n+1)2+(n+1)+1=√n2+n+1n2+3n+3<1 ∀n∈ℕ*
⇒un+1<un ∀≥1⇒ dãy (un) là dãy số giảm.
Mặt khác: 0<un<1⇒ dãy (un) là dãy bị chặn.
Chọn đáp án C
Câu 24:
19/07/2024Cho một cấp số cộng có u1=−3; u6=27. Tìm d ?
 Xem đáp án
Xem đáp án
Ta có:
u6=27⇔u1+5d=27⇔−3+5d=27⇔5d=30⇔d=6
Chọn đáp án B
Câu 25:
19/07/2024Cho cấp số cộng (un) thỏa mãn: {u5+3u3−u2=−213u7−2u4=−34
Tính số hạng thứ 100 của cấp số
 Xem đáp án
Xem đáp án
Từ giả thiết bài toán, ta có: {u1+4d+3(u1+2d)−(u1+d)=−213(u1+6d)−2(u1+3d)=−34
⇔{3u1+9d=−21u1+12d=−34⇔{u1=2d=−3
Số hạng thứ 100 của cấp số: u100=u1+99d=2+99. (−3)=−295
Chọn đáp án B
Câu 26:
20/07/2024Cho các số - 4;1 ; 6; x theo thứ tự lập thành một cấp số cộng. Tìm x?
 Xem đáp án
Xem đáp án
Vì các số -4; 1; 6; x theo thứ tự u1, u2, u3, u4 lập thành cấp số cộng nên:
u4−u3=u3−u2⇒x−6=6−1⇔x=11
Chọn đáp án D.
Câu 27:
19/07/2024Biết các số C1n; C2n; C3n theo thứ tự lập thành một cấp số cộng với n>3. Tìm n?
 Xem đáp án
Xem đáp án
Ba số C1n; C2n; C3n theo thứ tự u1, u2, u3 lập thành cấp số cộng nên
u1+u3=2u2⇔C1n+C3n=2C2n (n≥3)⇔n!(n−1)!.1!+ n!(n−3)!.3!=2. n!(n−2)!.2!⇔n+(n−2)(n−1)n6=2.(n−1)n2⇔1+n2−3n+26=n−1⇔n2−9n+14⇔[n=2n=7⇔n=7 (n≥3).
Chọn đáp án B.
Câu 28:
21/07/2024Cho cấp số cộng (un) có u3 = 15 và d= -2. Tìm un ?
 Xem đáp án
Xem đáp án
Ta có {15=u3=u1+2dd=−2⇔{u1=19d=−2
⇒un=u1+(n−1)d=19 + (n−1).(−2)=−2n+21.
Chọn đáp án A
Câu 29:
19/07/2024Cho cấp số cộng (un) có u1 = -5 và d= 3. Số 100 là số hạng thứ mấy của cấp số cộng?
 Xem đáp án
Xem đáp án
{u1=−5d=3n↔un=100→100=un=u1+(n−1)d= −5+(n−1).3⇔100=3n−8⇔3n=108⇔n= 36
Chọn đáp án D
Câu 30:
22/07/2024Cho cấp số cộng (un) thỏa mãn u2+u8+u9+u15=100.Tính tổng 16 số hạng đầu tiên của cấp số cộng đã cho.
 Xem đáp án
Xem đáp án
Ta có: u2+u8+u9+u15=100
⇔u1+d+ u1+7d+ u1+8d+u1+14d= 100⇔4u1+30d=100⇔2u1+15d=50.
Khi đó S16=162(2u1+15d)=8.50=400
Chọn đáp án D.
Câu 31:
19/07/2024Nếu 1b+c; 1c+a; 1a+b theo thứ tự lập thành cấp số cộng thì dãy số nào sau đây lập thành cấp số cộng?
 Xem đáp án
Xem đáp án
Theo giả thiết 1b+c; 1c+a; 1a+b theo thứ tự lập thành cấp số cộng nên
2c+a=1b+c+1a+b⇔2c+a= a+b +b+ c(b+c).(a+b)⇔c+a2=(b+c)(b+a)a+c+2b⇔(a+c)2+2b(c+a)=2(b2+ab+bc+ac)⇔a2+c2+2ac+2bc+2bc=2(b2+ab+bc+ac)⇔a2+c2=2b2.
Chọn đáp án C.
Câu 32:
19/07/2024Trong các dãy số sau, dãy số nào là một cấp số nhân?
 Xem đáp án
Xem đáp án
Dãy (un) là cấp số nhân
⇔un=qun−1 (n∈ℕ*)⇔u2u1=u3u2=u4u3=⋯=q (un=0), q là công bội.
Xét đáp án A: 128; −64; 32; −16; 8; ...⇒u2u1=−12=u3u2=u4u3⇒Chọn A.
Xét đáp án B: √2; 2; 4; 4√2; ....⇒u2u1=1√2=2=u3u2⇒loại B.
Tương tự, ta cũng loại các đáp án C, D.
Chọn đáp án A.
Câu 33:
19/07/2024Dãy số nào sau đây không phải là cấp số nhân?
 Xem đáp án
Xem đáp án
Các đáp án A, B, C đều là các cấp số nhân công bội lần lượt là 2; 3; 12
Xét đáp án D: 1π; 1π2; 1π4; 1π6; ⋯⇒u2u1=1π=1π2=u3u2
Chọn đáp án D.
Câu 34:
20/07/2024Cho cấp số nhân 12; 14; 18; ⋯; 14096. Hỏi số 14096 là số hạng thứ mấy trong cấp số nhân đã cho?
 Xem đáp án
Xem đáp án
Cấp số nhân: 12; 14; 18; ⋯; 14096 ⇒{u1=12q=u2u1=12⇒un=12.(12)n−1=12n.
un=14096⇔12n=1212⇔n=12
Chọn đáp án B.
Câu 35:
23/07/2024Với giá trị x nào dưới đấy thì các số - 4; x; -9 theo thứ tự đó lập thành một cấp số nhân?
 Xem đáp án
Xem đáp án
Để ba số - 4 ; x ; - 9 theo thứ tự lập thành cấp số nhân khi và chỉ khi :
x2= (−4).(−9)= 36⇔x= ±6
Chọn đáp án C.
Câu 36:
27/11/2024Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp 27 lần góc nhỏ nhất. Tổng của góc lớn nhất và góc bé nhất bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là C
Lời giải
Giả sử 4 góc A, B, C, D (với A< B< C< D) theo thứ tự đó lập thành cấp số nhân thỏa yêu cầu với công bội q. Ta có
{A+B+C+D=360D=27A⇔{A(1+q+q2+q3)=360Aq3=27A⇔{q=3A=9D=Aq3=243⇒A+D=9+ 243 = 252.
*Phương pháp giải:
Cho cấp số nhân (un)với công bội q≠1. Đặt Sn=u1+u2+u3+...+un. Khi đó
Sn=u1(1−qn)1−q
*Lý thuyết:
Cấp số nhân là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng ngay trước nó với một số không đổi q.
Số q được gọi là công bội của cấp số nhân.
Cấp số nhân (un)với công bội q được cho bởi hệ thức truy hồi
un=un−1.q,n∈N∗
* Chú ý: Dãy (un) là cấp số nhân thì uk2=uk−1.uk+1(k≥2).
2. Số hạng tổng quát
Nếu một cấp số nhân có số hạng đầu u1 và công bội q thì số hạng tổng quát uncủa nó được xác định bởi công thức
un=u1.qn−1,n≥2
3. Tổng của n số hạng đầu của một cấp số nhân
Cho cấp số nhân (un)với công bội q≠1. Đặt Sn=u1+u2+u3+...+un. Khi đó
Sn=u1(1−qn)1−q

Xem thêm
Câu 37:
23/10/2024Trên một bàn cờ có nhiều ô vuông, người ta đặt 7 hạt dẻ vào ô đầu tiên, sau đó đặt tiếp vào ô thứ hai số hạt nhiều hơn ô thứ nhất là 5, tiếp tục đặt vào ô thứ ba số hạt nhiều hơn ô thứ hai là 5,… và cứ thế tiếp tục đến ô thứ n. Biết rằng đặt hết số ô trên bàn cờ người ta phải sử dụng 25450 hạt. Hỏi bàn cờ đó có bao nhiêu ô vuông?
 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Phương pháp giải:
- bài toán CSC có: u1 = 7 và d = 5
- áp dụng công thức cấp số cộng để tính ra số ô vuông trên bàn cờ
*Lời giải:
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng (un) có u1=7, d=5.
Gọi n là số ô trên bàn cờ thì u1+u2+⋯+un=25450=Sn.
Ta có 25450=Sn=nu1+n(n−1)2d=7n+n2−n2.5
⇔5n2+9n−50900=0⇔n=100
*Lý thuyết cần nắm và các phép toán về cấp số cộng, cấp số nhân:
1) Cấp số cộng là một dãy số ,trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Tức là:
un=un−1+d,n≥2
Số d được gọi là công sai của cấp số cộng.
- Nếu (un) là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:
Số hạng tổng quát
Nếu cấp số cộng có số hạng đầu là và công sai d thì số hạng tổng quát của nó được xác định theo công thức
Tổng n số hạng đầu của một cấp số cộng
Cho cấp số cộng với công sai d. Đặt . Khi đó
2) Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng ngay trước nó với một số không đổi q. Tức là:
Số q được gọi là công bội của cấp số nhân.
* Chú ý: Dãy là cấp số nhân thì .
Số hạng tổng quát
Nếu một cấp số nhân có số hạng đầu và công bội q thì số hạng tổng quát của nó được xác định bởi công thức
Tổng của n số hạng đầu của một cấp số nhân
Cho cấp số nhân với công bội . Đặt . Khi đó
Xem thêm các bài viết liên quan hay, chi tiết:
Có thể bạn quan tâm
- 93 Bài tập trắc nghiệm Lượng giác lớp 11 có lời giải (P1) (1661 lượt thi)
- Bài tập Lượng giác ôn thi đại học có lời giải (P1) (377 lượt thi)
- 160 bài trắc nghiệm Giới hạn từ đề thi đại học có đáp án (P1) (1317 lượt thi)
- Bài tập Giới hạn ôn thi đại học có lời giải (P1) (781 lượt thi)
- 15 câu lượng giác cơ bản , nâng cao (có đáp án) (p1) (353 lượt thi)
- Bài tập Lượng giác từ đề thi Đại học cơ bản, nâng cao (P1) (1038 lượt thi)
- 299 câu trắc nghiệm Tổ hợp xác suất từ đề thi đại học có lời giải chi tiết(P1) (3411 lượt thi)
- Bài tập Tổ Hợp - Xác Suất từ đề thi đại học cực hay có lời giải (P1) (1554 lượt thi)
- Bài tập Phép dời hình và phép đồng dạng trong mặt phẳng từ đề thi Đại Học (P1) (369 lượt thi)
- Bài tập Lượng giác từ đề thi đại học cơ bản, nâng cao có đáp án (P1) (1085 lượt thi)