Trắc nghiệm Ôn chương 2 - hình học (có đáp án)
Trắc nghiệm Toán 11 Ôn tập chương 2 Hình học
-
602 lượt thi
-
30 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
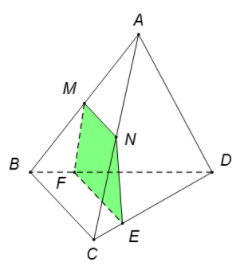
Ta có E là điểm chung của hai mặt phẳng (MNE) và (BCD).
Lại có {MN⊂(MNE)BC⊂(BCD)MN∥BC
→ Giao tuyến của hai mặt phẳng (MNE) và (BCD) là đường thẳng d đi qua điểm E và song song với BC và MN
Trong mặt phẳng (BCD), gọi F=d∩BC.
Khi đó thiết diện tạo bởi mặt phẳng (MNE) và tứ diện ABCD là hình thang MNEF với F là điểm trên cạnh BD mà EF∥BC.
Câu 2:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
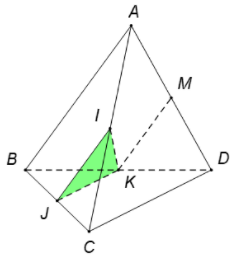
Ta có
{(IJK)∩(ABD)=KIJ⊂(IJK),AB⊂(ABD)IJ∥AB
→(IJK)∩(ABD)=KM∥IJ∥AB.
Câu 3:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải.
Đáp án B, C sai. Hai đường thẳng lần lượt nằm trên hai mặt phẳng song song với nhau thì có thể chéo nhau.
Đáp án D sai vì qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được vô số đường thẳng song song với mặt phẳng cho trước đó
Câu 4:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
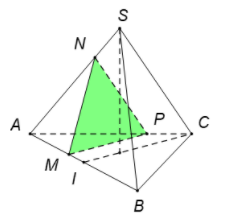
Để ý hai tam giác MNP và SIC đồng dạng với tỉ số AMAI=2xa
→CMNPCSIC=2xa
⇔CMNP=2xa(SI+IC+SC)
=2xa(a√32+a√32+a)
=2x(√3+1).
Câu 5:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
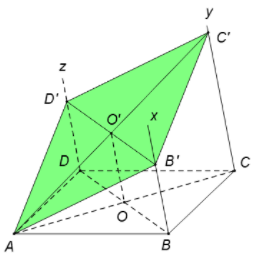
Gọi O là tâm của hình bình hành ABCD. Dựng đường thẳng qua O song song và cắt tại
Theo cách dưng trên, ta có là đường trung bình của hình thang
Ngoài ra ta có là đường trung bình của tam giác
Câu 6:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải.
Đáp án B sai: hai đường thẳng đó có thể song song nhau.
Đáp án C sai: hai đường thẳng đó có thể cắt nhau.
Đáp án D sai: hai đường thẳng đó có thể song song hoặc cắt nhau.
Câu 7:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
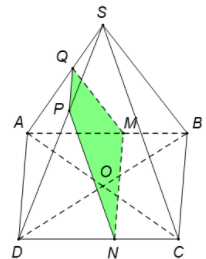
Lần lượt lấy các điểm thuộc các cạnh thỏa .
Suy ra và .
Theo cách dựng trên thì thiết diện là hình thang.
Câu 8:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
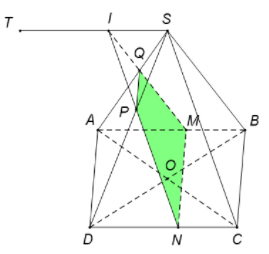
Lần lượt lấy các điểm thuộc các cạnh thỏa .
Suy ra và .
Vì
I nằm trên đường thẳng là giao tuyến của hai mặt phẳng và .
Khi với T là điểm thỏa mãn tứ giác ABST là hình bình hành.
Vậy quỹ tích cần tìm là đoạn thẳng song song với AB.
Câu 9:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
A. Sửa lại cho đúng: Ba điểm không thẳng hàng.
B. Sửa lại cho đúng: Một điểm và một đường thẳng không chứa điểm đó.
Câu 10:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
A. Sửa lại cho đúng: a và b không có điểm chung và không đồng phẳng.
B. Sửa lại cho đúng: a và b là hai cạnh đối của một hình tứ diện.
C. Sai vì a và b có thể song song.
Câu 11:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
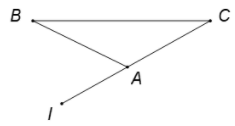
Ta có
Câu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
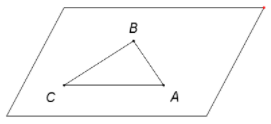
Ta có ABC là tam giác ba điểm A,B,C không thẳng hàng. Vậy có duy nhất một mặt phẳng chứa A,B,C .
Câu 13:
22/07/2024Trong không gian cho bốn điểm không đồng phẳng, có thể xác định nhiều nhất bao nhiêu mặt phẳng phân biệt từ các điểm đó?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
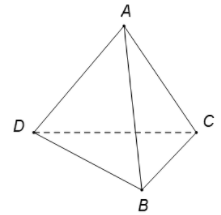
Giả sử bốn điểm đó là tứ diện ABCD.
Có các mặt phẳng đó là:
Câu 14:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
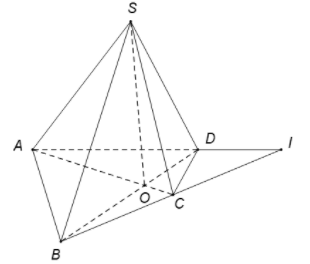
Ta có
Câu 15:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải.
Hình chóp tứ giác có tất cả 5 mặt nên thiết diện không thể là lục giác.
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
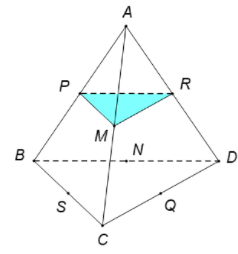
Dễ thấy mà
Vậy không đồng phẳng.
Câu 18:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Hai đường thẳng a và b chéo nhau có duy nhất một mặt phẳng chứa a và song song với b
Câu 19:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải.
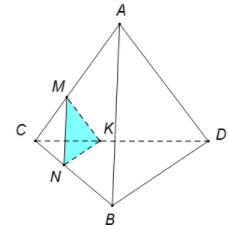
Ta có
với
Tương tự ta có
với
Vậy thiết diện của với tứ diện ABCD là tam giác MNK
Câu 20:
22/11/2024Có bao nhiêu cạnh của hình lập phương chéo nhau với đường chéo của hình lập phương?
 Xem đáp án
Xem đáp án
Đáp án đúng: D
* Lời giải:
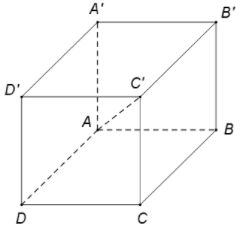
Các cạnh chéo nhau với đường chéo của hình lập phương là: A'B', A'D', DD', CD, BC, BB'
* Phương pháp giải:
- Nắm lại tính chất về đường thẳng chéo nhau trong mặt phẳng không gian
*Một số lý thuyết và dạng bài tập về đường thẳng và mặt phẳng trong không gian:
1.Điểm thuộc mặt phẳng.
Cho điểm A và mặt phẳng (α).
- Khi điểm A thuộc mặt phẳng (α) ta nói A nằm trên (α) hay (α) chứa A, hay (α) đi qua A và kí hiệu là .
- Khi điểm A không thuộc mặt phẳng (α) ta nói điểm A nằm ngoài (α) hay (α) không chứa A và kí hiệu là .
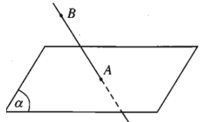
Hình trên cho ta hình biểu diễn của điểm A thuộc mặt phẳng , còn điểm B không thuộc (α).
2. Các tính chất thừa nhận về đường thẳng và mặt phẳng trong không gian
- Tính chất 1. Có một và chỉ một đường thẳng đi qua hai điểm phân biệt
- Tính chất 2. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.
Một mặt phẳng hoàn toàn xác định nếu biết nó đi qua ba điểm không thẳng hàng. Ta kí hiệu mặt phẳng đi qua ba điểm không thẳng hàng A, B, C là mặt phẳng (ABC) hoặc mp(ABC) hoặc (ABC).
- Tính chất 3. Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (α) thì ta nói đường thẳng d nằm trong (α) hay (α) chứa d và kí hiệu là hay .
- Tính chất 4. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.
Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng, còn nếu không có mặt phẳng nào chứa các điểm đó thì ta nói chúng không đồng phẳng.
- Tính chất 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.
Từ đó suy ra: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy.
Đường thẳng chung d của hai mặt phẳng phân biệt (α) và (β) được gọi là giao tuyến của (α) và (β) và kí hiệu là .
- Tính chất 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng
3. Vị trí tương đối của hai đường thẳng trong không gian.
Cho hai đường thẳng a và b trong không gian. Khi đó có thể xảy ra một trong các trường hợp sau:
- Trường hợp 1. Có một mặt phẳng chứa a và b.
Khi đó, ta nói a và b đồng phẳng. Theo kết quả của hình học phẳng có 3 khả năng xảy ra:
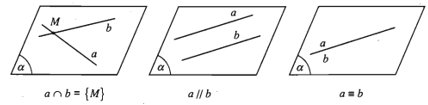
i) a và b có điểm chung duy nhất M. Ta nói a và b cắt nhau tại M và kí hiệu . Ta có thể viết .
ii) a và b không có điểm chung. Ta nói a và b song song với nhau và kí hiệu là a // b.
iii) a trùng b, kí hiệu là .
- Trường hợp 2. Không có mặt phẳng nào chứa a và b.
Khi đó ta nói a và b chéo nhau hay a chéo với b.
4. Tính chất về đường thẳng song song và đường thẳng chéo nhau trong không gian
- Định lí. Trong không gian, qua một điểm không nằm trên đường thẳng cho trước, có một và chỉ một đường thẳng song song với đường thẳng đã cho.
- Định lí (về giao tuyến của ba mặt phẳng).
Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đôi một song song với nhau.
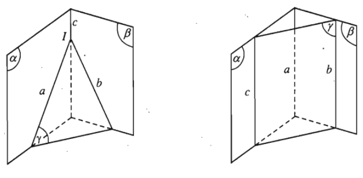
- Hệ quả. Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
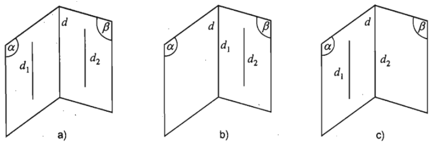
5. Vị trí tương đối của đường thẳng và mặt phẳng.
Cho đường thẳng d và mặt phẳng (α). Tùy theo số điểm chung của d và (α), ta có ba trường hợp sau:
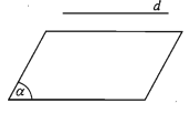
- d và (α) không có điểm chung. Khi đó ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) // d.
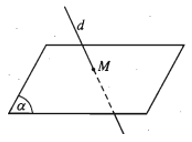
- d và (α) chỉ có một điểm chung duy nhất M. Khi đó ta nói d và (α) cắt nhau tại điểm M và kí hiệu .
- d và (α) có từ hai điểm chung trở lên. Khi đó, d nằm trong (α) hay (α) chứa d và kí hiệu .
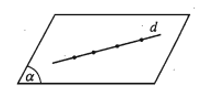
6. Tính chất về đường thẳng và mặt phẳng song song
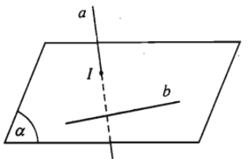
- Định lí. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).
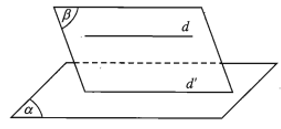
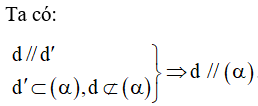
- Định lí. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với a.
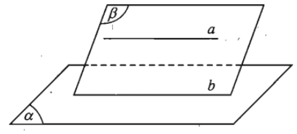
- Hệ quả. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Định lí. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Ôn tập chương 2 - Hình học (mới 2024 + Bài Tập) - Toán 11
Câu 21:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Hai đường thẳng phân biệt a và b trong không gian có ba vị trí tương đối là: cắt nhau, song song, chéo nhau.
Câu 22:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải.
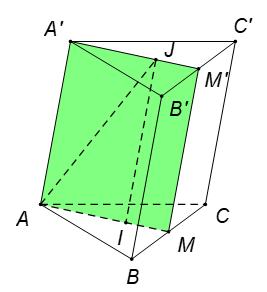
Kéo dài AI cắt BC tại M, suy ra M là trung điểm BC.
Ta có
Trong mặt phẳng , gọi .
Khi đó thiết diện là tứ giác , tứ giác này có là hình bình hành.
Câu 23:
23/07/2024Cho tứ diện đều SABC. Gọi I là trung điểm của đoạn AB, M là điểm di động trên đoạn AI. Qua M vẽ mặt phẳng song song với Thiết diện tạo bởi với tứ diện SABC là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải.
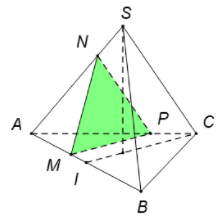
Gọi N,P lần lượt nằm trên các cạnh SA, AC sao cho
. Vậy thiết diện là tam giác MNP .
Tứ diện SABC đều nên tam giác SIC cân tại I.
Ngoài ra ta có .
Suy ra tam giác MNP cân tại M.
Câu 24:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Hai đường thẳng phân biệt cùng nằm trong một mặt phẳng có hai vị trí tương đối là: cắt nhau, song song.
Câu 25:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải.
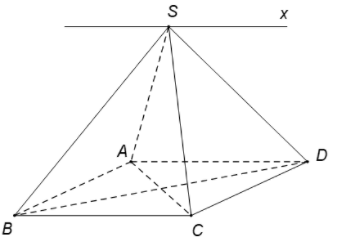
Ta có
Câu 26:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
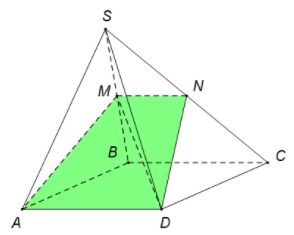
Ta có nên
với
Tứ giác AMND có là hình thang.
Câu 27:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
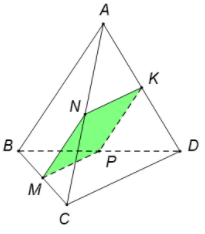
Ta có
với
Tương tự ta có
với
+
với
+
Do đó và là hình bình hành.
Câu 28:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Đường thẳng a song song với mặt phẳng khi chúng không có điểm chung.
Câu 30:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải.
Trong không gian hai mặt phẳng phân biệt và có hai vị trí tương đối là: cắt nhau hay song song.
Có thể bạn quan tâm
- Trắc nghiệm Ôn chương 2 - hình học (có đáp án) (601 lượt thi)
- 100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (1579 lượt thi)
- 100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1) (1359 lượt thi)
- Trắc nghiệm Ôn tập Toán 11 Chương 2 Hình học có đáp án (361 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Đường thẳng và mặt phẳng song song (có đáp án) (1207 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song (có đáp án) (1051 lượt thi)
- Trắc nghiệm Hai mặt phẳng song song (có đáp án) (804 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án) (643 lượt thi)
- Trắc nghiệm Phép chiếu song song. Hình biểu diễn của một hình không gian (có đáp án) (604 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (578 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (Vận dụng) (478 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Thông hiểu) (473 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (473 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Nhận biết) (471 lượt thi)
