Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
-
436 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Có bao nhiêu cách chọn ra ba đỉnh từ các đỉnh của một hình lập phương để thu được một tam giác đều?
Xem đáp án
Nối các đường chéo của các mặt ta được 2 tứ diện đều không có đỉnh nào chung
Mỗi tứ diện đều có 4 mặt là 4 tam giác đều. Nên tổng cộng có 8 tam giác đều.
Đáp án cần chọn là: D
Câu 2:
13/07/2024Cho hình đa diện đều loại {4;3} có cạnh bằng a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Mệnh đề nào dưới đây là đúng?
Xem đáp án
Khối đa diện đều loại {4;3} là hình lập phương. Khối lập phương có 6 mặt là hình vuông cạnh a.
Diện tích một mặt là
Vậy tổng diện tích các mặt của hình lập phương đó là:
Đáp án cần chọn là: C
Câu 3:
22/07/2024Cho hình bát diện đều cạnh 2. Gọi S là tổng diện tích tất cả các mặt bên của hình bát diện đó. Khi đó S bằng:
Xem đáp án
Bát diện đều là hình có 8 mặt là tam giác đều, các mặt là tam giác đều cạnh 2.
Diện tích một mặt là
Vậy tổng diện tích các mặt của hình bát diện đó là
Đáp án cần chọn là: B
Câu 4:
23/07/2024Tính tổng diện tích tất cả các mặt của khối đa diện đều loại {3;5} có các cạnh bằng 1
Xem đáp án
Khối đa diện đều loại {3;5} là khối 20 mặt đều.
Khối 20 mặt đều thì 1 mặt là tam giác đều cạnh bằng 1 có diện tích một mặt bằng:
Vậy diện tích tất cả các mặt của khối đa diện là
Đáp án cần chọn là: D
Câu 5:
26/11/2024Diện tích toàn phần của hình bát diện đều cạnh bằng 2a là:
Xem đáp án
Đáp án đúng: B
*Lời giải:
Tam giác đều có cạnh bằng 2a có diện tích
Vậy diện tích toàn phần của bát diện đều là
*Phương pháp giải:
- Diện tích khối bát diện đều = 8. diện tích một mặt tam giác đều. Do 8 mặt đều là tam giác đều cạnh 2a
*Lý thuyết nắm thêm về khối đa diện
Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
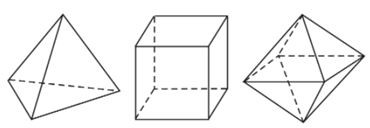
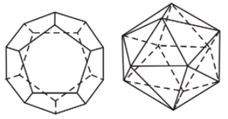
Bảng tóm tắt của năm loại khối đa diện đều.
Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khối đa diện lồi và khối đa diện đều (mới 2024 + Bài Tập) – Toán 12
50 Bài tập Khối đa diện lồi và khối đa diện đều Toán 12 mới nhất
Câu 6:
13/07/2024Cho khối chóp S.ABC. Trên các cạnh SA, SB, SC lấy các điểm A’, B’, C’ sao cho , khi đó tồn tại một phép vị tự biến khối chóp S.ABC thành khối chóp S.A’B’C’ với tỉ số đồng dạng là:
Xem đáp án
Ta có:
Do đó phép vị tự tâm S tỉ số biến các điểm A, B, C thành A’, B’, C’
Câu 7:
23/07/2024Mệnh đề nào sau đây là mệnh đề đúng?
Xem đáp án
Đa diện đều có tất cả các mặt là các đa giác bằng nhau.
Không tồn tại đa diện đều có 5 và 6 đỉnh, do đó chóp S.ABCD và lăng trụ ABC.A’B’C’ không thể là đa diện đều.
Nếu mỗi đỉnh là đỉnh chung của đúng 3 mặt thì nó cũng là đỉnh chung của đúng 3 cạnh. Giả sử số đỉnh của đa diện là n thì số cạnh của nó phải là (vì mỗi cạnh được tính 2 lần), do đó n chẵn
Đáp án cần chọn là: C