25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 12 Bài 1: Khái niệm về mặt tròn xoay

Câu 1:

A.

$α = 0 °$

B.

$α = 50 °$

C.

$α = 90 °$

D.

$α = 180 °$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Trong mặt phẳng (P) cho hai đường thẳng d, d’ cắt nhau tại O và tạo thành góc $α (0 ° < α < 90 °)$

Khi quay mặt phẳng (P) xung quanh d thì đường thẳng d’ sinh ra một mặt được gọi là mặt nón tròn xoay (gọi tắt là mặt nón).

Do đó điều kiện để có được mặt nón tròn xoay là góc $0 ° < α < 90 °$

Câu 2:

19/07/2024

Cho hai điểm M, N cố định và đường thẳng

$Δ$ cố định thỏa mãn

$M N ⊥ Δ$ ,

$d (M, Δ) = d (N, Δ)$ . Có bao nhiêu đường tròn đi qua M, N và nhận

$Δ$ làm trục?

A. 1

B. 2

C. 0

D. Vô số

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Gọi (P) là mặt phẳng chứa MN và vuông góc $Δ, O = (P) \cap Δ$ . Khi đó MO = NO nên M, N nằm trên đường tròn tâm O bán kính OM.

Do M, N, cố định nên (P), O cố định và (O,OM) cố định và duy nhất

Câu 3:

22/07/2024

Quay hình vuông ABCD quanh trục AC ta được:

A. 2 hình nón

B. 1 hình trụ

C. 2 hình trụ

D. 1 hình cầu

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

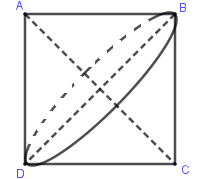
Quan sát hình vẽ ta thấy khi quay hình vuông ABCD quanh trục AC ta được 2 hình nón.

Câu 4:

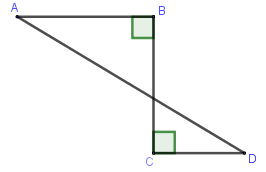
21/07/2024

Hình ABCD khi quay quanh BC thì tạo ra:

A. Một hình trụ

B. Một hình nón

C. Một hình nón cụt

D. Hai hình nón

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

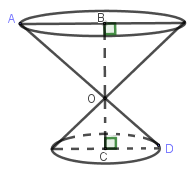
Gọi O là giao điểm của AD và BC.

- Quay tam giác vuông ABO quanh BO ta được một hình nón.

- Quay tam giác vuông DCO quanh CO ta được một hình nón.

Vậy có tất cả hai hình nón được tạo thành.

Câu 5:

19/07/2024

Cho tam giác AOB vuông tại O. Quay tam giác quanh cạnh OA ta được hình nón có đường sinh và đường cao lần lượt là:

A. AB, OA

B. AB, OB

C. OA, OB

D. OB, OA

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

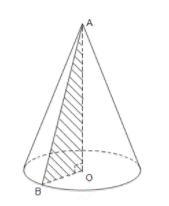
Quan sát hình vẽ ta thấy đường sinh là AB và đường cao AO

Câu 6:

16/07/2024

Trục đường tròn là đường thẳng đi qua tâm và:

A. Vuông góc với một bán kính đường tròn

B. Vuông góc với một đường kính đường tròn

C. Vuông góc với mặt phẳng chứa đường tròn

D. Vuông góc với mặt phẳng chứa một đường kính

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Trục của đường tròn là đường thẳng vuông góc với mặt phẳng chứa đường tròn tại tâm của nó.

Câu 7:

18/07/2024

Thiết diện qua trục của một khối nón là một tam giác vuông cân và có cạnh góc vuông bằng

$a \sqrt{2}$ . Thể tích V của khối nón bằng:

A.

$\frac{π a^{3} \sqrt{3}}{3}$

B.

$\frac{π a^{3}}{3}$

C.

$\frac{4 π a^{3}}{3}$

D.

$\frac{2 π a^{3}}{3}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

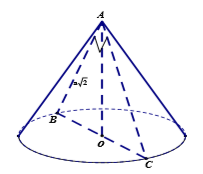
Giả sử thiết diện qua trục là tam giác ABC, theo bài ra ta có $Δ A B C$ vuông cân tại A, có $A B = a \sqrt{2}$

$\Rightarrow B C = A B \sqrt{2} = 2 a$

$\Rightarrow$ Bán kính đáy của hình nón là: $r = \frac{1}{2} B C = a$ và chiều cao hình nón là $h = O A = \frac{1}{2} B C = a$

Vậy thể tích khối nón là: $\Rightarrow V = \frac{1}{3} π r^{2} h = \frac{1}{3} π a^{2} . a = \frac{π a^{3}}{3}$

Câu 8:

17/07/2024

Một hình nón có bán kính đáy bằng 1, chiều cao nón bằng 2. Khi đó góc ở đỉnh của nón là thỏa mãn:

A.

$\tan φ = \frac{\sqrt{5}}{5}$

B.

$\cot φ = \frac{\sqrt{5}}{5}$

C.

$\cos φ = \frac{2 \sqrt{5}}{5}$

D.

$\sin φ = \frac{2 \sqrt{5}}{5}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

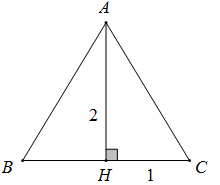
Giả sử thiết diện qua trục của hình nón đã cho là $Δ A B C$ cân tại A với A là đỉnh nón, BC là đường kính đáy của nón.

Gọi H là tâm đáy nón

$\Rightarrow$ H là trung điểm BC, $A H ⊥ B C$

Ta có: $H B = H C = 1, A H = 2$

Ta có: $2 φ = \hat{B A C} \Rightarrow α = \hat{H A C}$

$A C = \sqrt{A H^{2} + H C^{2}} = \sqrt{5}$

$\cos φ = \frac{A H}{A C} = \frac{2}{\sqrt{5}} = \frac{2 \sqrt{5}}{5}$

Câu 9:

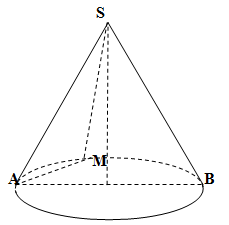
22/07/2024

Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là $135 °$ . Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí N để diện tích SAM đạt giá trị lớn nhất.

A. Vô số

B. 3

C. 2

D. 1

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Ta có:

$S_{S A M} = \frac{1}{2} S A . S M \sin \hat{A S M}$

$= \frac{1}{2} S A^{2} \sin \hat{A S M} \leq \frac{1}{2} S A^{2}$

$\Rightarrow \max S_{S A M} = \frac{1}{2} S A^{2}$

Dấu “=” xảy ra khi $\sin \hat{A S M} = 1$

$\Leftrightarrow \hat{A S M} = 90 °$

Có 2 điểm M như vậy (hai điểm đối xứng với nhau qua AB)

Câu 10:

21/07/2024

Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng 75% thể tích kem đóng băng ban đầu. Gọi h và r lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số

$\frac{h}{r}$

A.

$\frac{h}{r} = 3$

B.

$\frac{h}{r} = 2$

C.

$\frac{h}{r} = \frac{4}{3}$

D.

$\frac{h}{r} = \frac{16}{3}$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Theo đầu bài ta có bán kính của khối cầu và khối nón đều bằng r

Từ dữ kiện đầu bài ta suy ra: $V_{n o n} = \frac{3}{4} . V_{c a u}$

$\Leftrightarrow \frac{1}{3} π r^{2} h = \frac{3}{4} . \frac{4}{3} π r^{3}$

$\Leftrightarrow \frac{h}{r} = 3$

Câu 11:

22/07/2024

Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.

A.

$\frac{7 π}{3}$

B.

$\frac{7 π}{6}$

C.

$\frac{14 π}{3}$

D.

$\frac{14 π}{9}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

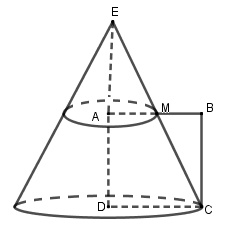
Kéo dài CM cắt DA tại E. Quay hình thang vuông AMCD quanh trục AD ta được hình nón cụt như hình vẽ.

Quay tam giác EDC quanh trục ED ta được hình nón.

Dễ thấy $V_{n c} = V_{1} - V_{2}$ , ở đó $V_{1}$ là thể tích khối nón đỉnh E, bán kính đáy DC = 2 và là thể tích khối nón đỉnh E, bán kính đáy AM = 1.

Có $\frac{E A}{E D} = \frac{A M}{D C} = \frac{1}{2}$

$\Rightarrow E A = A D = 2 \Rightarrow E D = 4$

$\Rightarrow V_{1} = \frac{1}{3} π D C^{2} . E D$

$= \frac{1}{3} π {.2}^{2} .4 = \frac{16 π}{3}$

$\Rightarrow V_{2} = \frac{1}{3} π A M^{2} . E A$

$= \frac{1}{3} π {.1}^{2} .2 = \frac{2 π}{3}$

Vậy $V = V_{1} - V_{2}$

$= \frac{16 π}{3} - \frac{2 π}{3} = \frac{14 π}{3}$

Câu 12:

13/07/2024

Cho hình chữ nhật ABCD có AB = 4 và AD = 3. Thể tích của khối trụ được tạo thành khi quay hình chữ nhật ABCD quanh cạnh AB bằng:

A.

$36 π$

B.

$12 π$

C.

$24 π$

D.

$48 π$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Khi quay hình chữ nhật ABCD quanh cạnh AB ta được khối trụ có chiều cao

$h = A B = 4;$ $r = A D = 3$

Vậy thể tích khối trụ là:

$V = π r^{2} h = π {.3}^{2} .4 = 36 π$

Câu 13:

13/07/2024

Mặt tròn xoay không thể có được nếu quay hình nào quanh một đường thẳng?

A. Đường thẳng

B. Parabol

C. Elip

D. Điểm

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Dựa vào định nghĩa ta thấy các đáp án A, B, C đều là các đường nên khi quay chúng quanh đường thẳng ta được mặt tròn xoay.

Đáp án D là một điểm nên khi quay ta chỉ được một đường tròn, do đó nó không là mặt tròn xoay.

Câu 14:

16/07/2024

Chọn phát biểu đúng:

Khi quay tam giác ABC vuông tại A quanh trục AB thì

A. AB là đường sinh

B. AB là đường cao

C. AB là bán kính đáy

D. AB là đường kính đáy

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

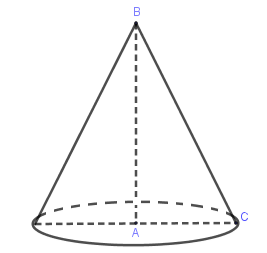
Quan sát hình vẽ ta thấy AB là đường cao

Câu 15:

15/07/2024

Cho hình trụ có trục

$Δ$ và bán kính R. Khi cắt hình trụ bởi mặt phẳng

$(α)$ song song với

$Δ$ và cách

$Δ$ một khoảng

$d (Δ; (α)) = k < R$ thì ta được thiết diện là:

A. Hình chữ nhật

B. Hình tròn

C. Hình elip

D. Đường sinh

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

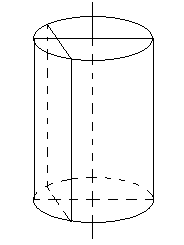
Khi cắt hình trụ bởi mặt phẳng song song với trục mà khoảng cách giữa và trục nhỏ hơn bán kính hình trụ thì ta được thiết diện là hình chữ nhật.

Câu 16:

15/07/2024

Gọi r, l, h lần lượt là bán kính đáy, độ dài đường sinh và chiều cao của hình nón. Chọn mệnh đề đúng:

A. r = h

B. h = l

C.

$r^{2} = h^{2} - l^{2}$

D.

$l^{2} = r^{2} + h^{2}$

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

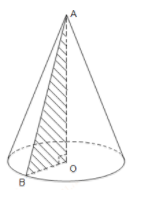
Quan sát hình vẽ ta thấy:

$l = A B, r = O B, h = A O$

Mà $A B^{2} = A O^{2} + O B^{2}$ nên $l^{2} = r^{2} + h^{2}$

Câu 17:

22/07/2024

Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bằng a. Thể tích của khối nón đã cho bằng:

A.

$\frac{\sqrt{3} π a^{3}}{3}$

B.

$\frac{\sqrt{3} π a^{3}}{2}$

C.

$\frac{2 π a^{3}}{3}$

D.

$\frac{π a^{3}}{3}$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

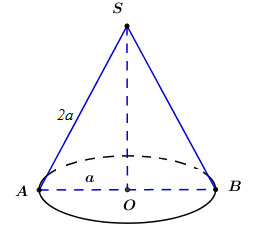
Xét $Δ S A O$ vuông tại O có:

$S O = \sqrt{S A^{2} - A O^{2}}$

$= \sqrt{{(2 a)}^{2} - a^{2}} = a \sqrt{3}$

Khi đó ta có: $V = \frac{1}{3} π R^{2} h$

$= \frac{1}{3} π . a^{2} . a \sqrt{3} = \frac{π a^{3} \sqrt{3}}{3}$

Câu 18:

18/07/2024

Hình trụ có bán kính r = 5cm và chiều cao h = 3cm có diện tích toàn phần gần với số nào sau đây?

A.

$251, 3 c m^{2}$

B.

$141, 3 c m^{2}$

C.

$172, 8 c m^{2}$

D.

$125, 7 c m^{2}$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Ta có:

$S_{t p} = 2 π r h + 2 π r^{2}$

$= 2 π .5.3 + 2 π {.5}^{2}$

$\approx 251, 3 c m^{2}$

Câu 19:

20/07/2024

Tính diện tích toàn phần của hình trụ có đường cao bằng 2 và đường kính đáy bằng 8

A.

$48 π$

B.

$160 π$

C.

$80 π$

D.

$24 π$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải:

Bán kính đáy của hình trụ đã cho là:

$r = \frac{d}{2} = \frac{8}{2} = 4$

Diện tích toàn phần của hình trụ đã cho là:

$S_{t p} = 2 π r h + 2 π r^{2}$

$= 2 π .2.4 + 2 π {.4}^{2} = 48 π$

Câu 20:

23/07/2024

Khi quay hình vẽ dưới đây quanh trục đối xứng là đường thẳng d thì ta được:

A. Hình trụ ngoại tiếp mặt cầu

B. Mặt cầu ngoại tiếp hình trụ

C. Hình nón nội tiếp mặt cầu

D. Hình trụ ngoại tiếp hình nón.

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

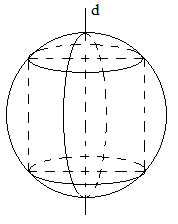
Quan sát hình vẽ ta thấy, khi quay hình vẽ ban đầu quanh đường thẳng d thì ta được hình trụ nội tiếp hình cầu hoặc hình cầu ngoại tiếp hình trụ.

Câu 21:

21/07/2024

Cho nửa đường tròn tâm O đường kính AB. Khi quay nửa đường tròn quanh AB ta được:

A. Nửa mặt cầu

B. Mặt cầu

C. Đường tròn

D. Hình tròn

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

Khi quay nửa đường tròn đường kính AB quanh trục AB ta được mặt cầu đường kính AB.

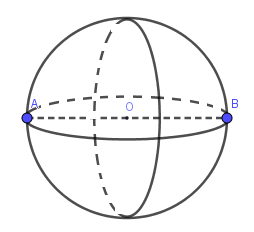
Câu 22:

21/07/2024

Cho hình chữ nhật ABCD, khi quay hình chữ nhật quanh cạnh AD thì CD được gọi là:

A. Chiều cao

B. Đường kính đáy

C. Chu vi đáy

D. Bán kính đáy

Xem đáp án

Đáp án: D

Giải thích:

Lời giải:

Quay hình chữ nhật ABCD quanh cạnh AD thì được hình trụ có chiều cao AD, đường sinh BC và bán kính đáy AB, CD.

Do đó CD được gọi là bán kính đáy.

Câu 23:

23/07/2024

Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là:

A.

$S_{x q} = \frac{1}{3} π r l$

B.

$S_{x q} = π r^{2} l$

C.

$S_{x q} = π r l$

D.

$S_{x q} = π r l + π r^{2}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải:

Công thức tính diện tích xung quanh hình nón có bán kính đáy r và độ dài đường sinh l là: $S_{x q} = π r l$

Câu 24:

18/07/2024

Cắt hình nón bởi một mặt phẳng qua trục thu được thiết diện là một tam giác vuông có diện tích bằng 8. Diện tích xung quanh của hình nón đã cho bằng:

A.

$16 \sqrt{2} π$

B.

$8 \sqrt{2} π$

C.

$4 \sqrt{2} π$

D.

$2 \sqrt{2} π$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

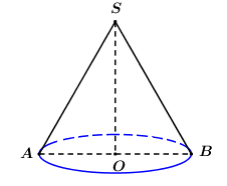
Giả sử thiết diện qua trục là tam giác SAB, O là tâm đường tròn đáy

$\Rightarrow$ O là trung điểm của AB.

Tam giác SAB vuông tại S nên

$S_{Δ S A B} = \frac{1}{2} S A . S B$

$= \frac{1}{2} S A^{2} = 8$

$\Leftrightarrow S A = 4 = l$

$\Rightarrow A B = S A \sqrt{2} = 4 \sqrt{2}$

$\Rightarrow r = O A = 2 \sqrt{2}$

Vậy diện tích xung quanh hình nón là

$S_{x q} = π r l$

$= π .2 \sqrt{2} .4$

$= 8 \sqrt{2} π$

Câu 25:

22/07/2024

Cho hình nón có góc ở đỉnh bằng

$120 °$ và đường cao bằng 2. Tính diện tích xung quanh của hình nón đã cho.

A.

$16 \sqrt{3} π$

B.

$8 \sqrt{3} π$

C.

$4 \sqrt{3} π$

D.

$8 π$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải:

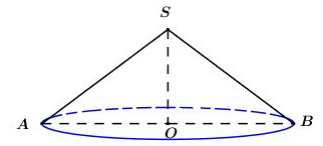
Gọi S là đỉnh hình nón, AB là 1 đường kính của hình nón và O là tâm đường tròn đáy của hình nón.

Khi đó ta có:

$\hat{A S B} = 120 °, h = S O = 2$

Ta có: $Δ S A B$ cân tại S suy ra SO là phân giác của $\hat{A S B}$

$\Rightarrow \hat{A S O} = \frac{1}{2} \hat{A S B} = 60 °$

Xét tam giác vuông SOA có:

$r = O A = S O . \tan 60 ° = 2 \sqrt{3},$

$l = S A = \frac{S O}{\cos 60 °} = 4$

Vậy diện tích xung quanh của hình nón là:

$S_{x q} = π r l$

$= π .2 \sqrt{3} .4$

$= 8 \sqrt{3} π$

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3