Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 10)
-
7649 lượt thi
-
12 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 2:
23/07/2024Cho 125 = ................... . Số thích hợp điền vào chỗ chấm là:
 Xem đáp án
Xem đáp án
0,0125
Đáp án B
Câu 3:
21/07/2024Trên bản đồ tỉ lệ 1 : 1000 có vẽ một mảnh đất hình chữ nhật với chiều dài 5cm; chiều rộng 3cm. Như vậy, mảnh đất đó có diện tích là:
 Xem đáp án
Xem đáp án
15
Đáp án A
Câu 4:
16/07/2024Một hình hộp chữ nhật có thể tích 216. Nếu tăng ba kích thước của hình hộp chữ nhật lên 2 lần, thì thể tích của hình hộp chữ nhật mới là:
 Xem đáp án
Xem đáp án
1728
Đáp án C
Câu 5:
19/07/2024Tam giác ABC, kéo dài BC thêm một đoạn CD =BC thì diện tích tam giác ABC tăng thêm 20. Diện tích tam giác ABC là :
 Xem đáp án
Xem đáp án
40
Đáp án D
Câu 6:
19/07/2024Hai số có tổng là số lớn nhất có 5 chữ số. Số lớn gấp 8 lần số bé. Như vậy, số lớn là:
 Xem đáp án
Xem đáp án
88888
Đáp án C
Câu 7:
21/07/2024Cho một số, nếu lấy số đó cộng với 0,75 rồi cộng với 0,25 được bao nhiêu đem cộng với 1, cuối cùng giảm đi 4 lần thì được kết quả bằng 12,5. Vậy số đó là:
 Xem đáp án
Xem đáp án
48
Đáp án B
Câu 8:
22/07/2024Khi đi cùng một quãng đường, nếu vận tốc tăng 25% thì thời gian sẽ giảm là:
 Xem đáp án
Xem đáp án
20%
Đáp án B
Câu 9:
17/12/2024Lúc 6 giờ sáng anh Ba đi bộ từ nhà lên tỉnh với vận tốc 5km/giờ. Lúc 7 giờ sáng anh Hai đi xe máy cũng đi từ nhà lên tỉnh với vận tốc 25 km/giờ. Như vậy, Anh Hai đuổi kịp anh Ba lúc:
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
Anh Hai xuất phát muộn hơn anh Ba số giờ là:
7h-6h=1(h)
Anh Ba đi được số km trước khi anh Hai xuất phát là:
5.1=5(km)
Anh Hai đuổi kịp anh ba mất số thời gian là:
5:(25-5)=0,25(h)=15 phút
Anh Hai đuổi kịp anh Ba lúc số giờ là:
7giờ +15 phút=7giờ 15 phút
*Phương pháp giải:
1. Tính khoảng cách mà anh Ba đã đi được trước khi anh Hai bắt đầu đi
2. Tính thời gian để anh Hai đuổi kịp anh Ba
3. Chuyển đổi thời gian từ giờ sang phút
*Lý thuyết:
1. Cách tính thời gian
Muốn tính thời gian ta lấy quãng đường chia cho vận tốc.
Gọi vận tốc là v, quãng đường là s, thời gian là t, ta có:
t = s : v
Chú ý:
- Đơn vị của thời gian sẽ tương ứng với đơn vị của quãng đường và vận tốc, ví dụ quãng đường có đơn vị là km, vận tốc có đơn vị đo là km/giờ thì thời gian có đơn vị là giờ; …
- Đơn vị của quãng đường và vận tốc phải tương ứng với nhau thì mới thực hiện được phép tính chia để tìm thời gian.
Ví dụ quãng đường có đơn vị làm, vận tốc có đơn vị là km/giờ, muốn tìm thời gian có đơn vị là giờ thì ta phải đổi quãng đường ra đơn vị làkm rồi mới áp dụng quy tắc để tính thời gian; hoặc phải đổi vận tốc từ ra đơn vị km/giờ ra đơn vị là m/giây, hay m/phút, … từ đó áp dụng quy tắc sẽ tính được thời gian tương ứng có đơn vị giây hoặc phút .
- Một số công thức cần nhớ:
+) Thời gian đi = thời gian đến – thời gian khởi hành – thời gian nghỉ (nếu có).
+) Thời gian đến = thời gian khởi hành + thời gian đi + thời gian nghỉ (nếu có).
+) Thời gian khởi hành = thời gian đến – thời gian đi – thời gian nghỉ (nếu có).
Xem thêm
Câu 10:
20/07/2024Cho hình vuông ABCD có cạnh 14cm ( hình bên). Như vậy, phần tô đen trong hình vuông ABCD có diện tích là:
 Xem đáp án
Xem đáp án
42,14
Đáp án C
Câu 11:
16/07/2024Vườn hoa nhà trường hình chữ nhật có chu vi 160m và chiều rộng bằng chiều dài. Người ta để diện tích vườn hoa để làm lối đi. Tính diện tích của lối đi.
 Xem đáp án
Xem đáp án
Nửa chu vi hình chữ nhật là: 160 : 2 = 80 ( m)
Chiều rộng hình chữ nhật là: ( 80 : 5 ) x 2 = 32 ( )
Chiều dài hình chữ nhật là: ( 80 : 5 ) x 3 = 48 ( )
Diện tích hình chữ nhật là: 32 x 48 = 1536 ( )
Diện tích lối đi là : 1536 : 24 = 64 ( )
Câu 12:
04/01/2025Cho tam giác ABC có cạnh AC dài 6cm , trên cạnh BC lấy điểm E, sao cho EB = EC. BH là đường cao hạ từ đỉnh B của tam giác ABC và BH = 3cm. EH chia tam giác ABC thành hai phần và diện tích tứ giác ABEH gấp đôi diện tích tam giác CEH.
a. Tính độ dài đoạn thẳng AH.
b. Tính diện tam giác AHE.
 Xem đáp án
Xem đáp án
Lời giải
a. Gọi S là diện tích:
Ta có:
Vì BE = EC và hai tam giác BHE, HEC có cùng chiều cao hạ từ đỉnh chung H nên
Do đó
Suy ra: và AC = 3HA ( vì hai tam giác ABC và BHA có cùng chiều cao hạ từ đỉnh chung B)
Vậy HA = = 6 : 3 = 2 ( cm)
Nghĩa là điểm H phải tìm cách A là 2cm
b. Ta có: = 6 x 3 : 2 = 9 ( )
Vì BE = EC và hai tam giác BAE, EAC có cùng chiều cao hạ từ đỉnh chung A, nên SBAE = SEAC do đó:
= 9 : 2 = 4,5 ()
Vì = 9 : 3 = 3 ()
Nên = 4,5 – 3 = 1,5 ()
*Phương pháp giải:
a) Dựa vào số lần gấp diện tích của 2 tam giác ABC và BHA
b)Áp dụng công thức diện tích tam giác
*Lý thuyết:
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
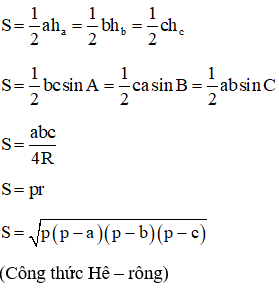
+ Phương pháp giải: Dựa vào dữ kiện bài ra để sử dụng linh hoạt một trong các công thức ở trên.
Xem thêm
Bài thi liên quan
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 1)
-
4 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 2)
-
5 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 3)
-
5 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 4)
-
4 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 5)
-
5 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 6)
-
4 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 7)
-
4 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 8)
-
4 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 9)
-
5 câu hỏi
-
45 phút
-
-
Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (Đề số 11)
-
4 câu hỏi
-
45 phút
-
Có thể bạn quan tâm
- Tổng hợp đề thi vào lớp 6 cực hay, có lời giải chi tiết (7648 lượt thi)
- 28 Đề ôn thi vào lớp 6 môn Toán cực hay (13057 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Ôn tập: Khái niệm về phân số có đáp án (388 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Ôn tập: So sánh hai phân số có đáp án (0 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Phân số thập phân có đáp án (1034 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Phép cộng và phép trừ hai phân số có đáp án (865 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Phép nhân và phép chia hai phân số có đáp án (821 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Hỗn số có đáp án (867 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Luyện tập chung có đáp án (665 lượt thi)
- Trắc nghiệm Bài tập Toán 5 Ôn tập và bổ sung về giải toán có đáp án (1036 lượt thi)
