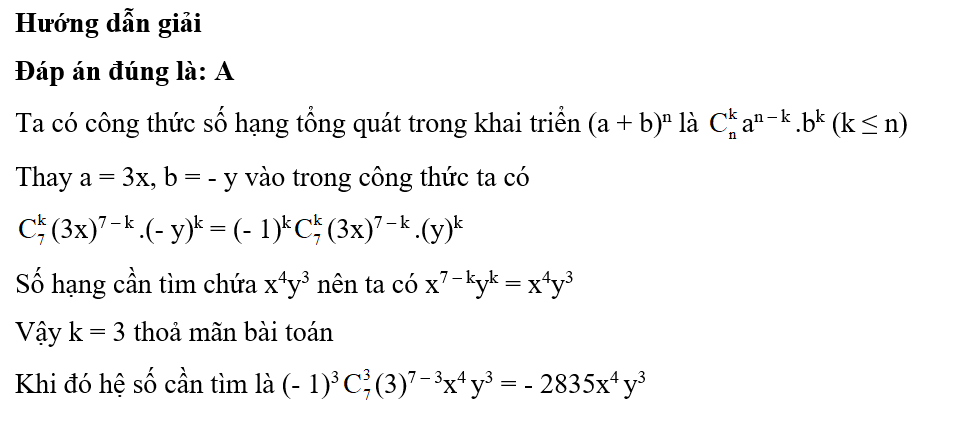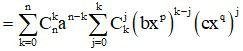Thi Online Trắc nghiệm Toán 10 Bài 25. Nhi thức Newton có đáp án
Trắc nghiệm Toán 10 Bài 25. Nhi thức Newton có đáp án
-
495 lượt thi
-
15 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Trong khai triển nhị thức (a + 2)n + 6 (n ℕ). Có tất cả 17 số hạng. Vậy n bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có trong khai triển (a + b)n có n + 1 số hạng.
Trong khai triển (a + 2)n + 6 (n ℕ) có tất cả 17 số hạng nên ta có n + 6 = 16.
Vậy n = 10.
Câu 2:
13/07/2024Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + b)7 bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có tổng số mũ của a, b trong mỗi hạng tử khi khai triển (a + b)n luôn bằng n.
Vậy tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + b)7 bằng 7.
Câu 3:
23/07/2024Biểu thức (5x)2(-6y2)7 là một số hạng trong khai triển nhị thức nào dưới đây
 Xem đáp án
Xem đáp án
Hướng dẫn giải.
Đáp án đúng là: C
Vì trong khai tiển (a + b)n thì trong mỗi số hạng tổng số mũ của a và b luôn bằng n Do đó, thay a = 5x, b = - 6y2 thì tổng số mũ của a và b bằng 9. Đáp án C đúng
Câu 4:
16/07/2024Số hạng tử trong khai triển (2x + y)6 bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có trong khai triển (a + b)n có n + 1 hạng tử.
Vậy trong khai triển (2x + y)6 có 7 hạng tử.
Câu 5:
14/07/2024Hệ số của x7 trong khai triển của (3 – x)9 là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a = 3, b = - x và n = 9 vào trong công thức ta có 39 – k .(- x)k = (- 1)k 39 – k .(x)k
Vì tìm hệ số của x7 nên ta có xk = x7 k = 7
Hệ số của x7 trong khai triển là (-1)7.32 = - 324.
Câu 6:
16/07/2024Hệ số của x5 trong khai triển (1 + x)12 bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a = 1, b = x và n = 12 vào trong công thức ta có 112 – k .(x)k = 112 – k .(x)k
Vì tìm hệ số của x5 nên ta có xk = x5 k = 5
Hệ số của x5 trong khai triển là .17 = 792.
Câu 7:
19/07/2024Trong khai triển nhị thức (2a – 1)6 ba số hạng đầu là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có khai triển
(2a – 1)6 = (2a)6(- 1)0 + (2a)5(- 1)1 + (2a)4(- 1)2 + (2a)3(- 1)3 + (2a)2(- 1)4 + (2a)1(- 1)5 + (2a)0(- 1)6
= 64a6 – 192a5 + 240a4 – 160a3 + 60a2 – 12a + 1
Vậy 3 số hạng đầu của khai triển là 64a6 – 192a5 + 240a4
Câu 8:
11/09/2024Khai triển nhị thức (2x + y)5 ta được kết quả là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Khai triển nhị thức
(2x + y)5 = (2x)5(y)0 + (2x)4(y)1 + (2x)3(y)2 + (2x)2(y)3 + (2x)(y)4 + (2x)0(y)5 = 32x5 + 80x4y + 80x3y2 + 40x2y3 + 10xy4 + y5 .
-> B đúng. A, C, D sai.
* Công thức nhị thức Newton (a + b)^n ứng với n = 4 ; n = 5 :
• (a + b)4 = a4 + a3b + a2b2 + ab3 + b4
= a4 + 4a3b + 6a2b2 + 4ab3 + b4.
• (a + b)5 = a5 + a4b + a3b2 + a2b3 + ab4 + b5
= a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5.
Xem thêm các bài viết liên quan hay, chi tiết khác:
Câu 10:
23/07/2024Trong khai triển số hạng không chứa x là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a = x, b = vào trong công thức ta có
(x)9 – k . = 8k= 8k x9-3k
Số hạng cần tìm không chứa x nên ta có 9 – 3k = 0
Vậy k = 3 thoả mãn bài toán
Khi đó hệ số cần tìm là (8)3 = 43008
Câu 11:
17/07/2024Trong khai triển (2x – 1)10 hệ số của số hạng chứa x8 là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a = 2x, b = - 1 vào trong công thức ta có
(2x)10 – k .(- 1)k = (-1)k(2)10-k(x)10 – k
Số hạng cần tìm chứa x8 nên ta có 10 – k = 8
Vậy k = 2 thoả mãn bài toán
Khi đó hệ số cần tìm là (- 1)2(2)8 = 11520.
Câu 12:
18/07/2024Khai triển nhị thức (2x + 3)4 ta được kết quả là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Khai triển nhị thức
(2x + 3)4 = (2x)4(3)0 + (2x)3(3)1 + (2x)2(3)2 + (2x)1(3)3 + (2x)0(3)4 = 16x4 + 96x3 + 216x2 + 216x + 81.
Câu 14:
15/11/2024Tìm số hạng không chứa x trong khai triển biết
 Xem đáp án
Xem đáp án
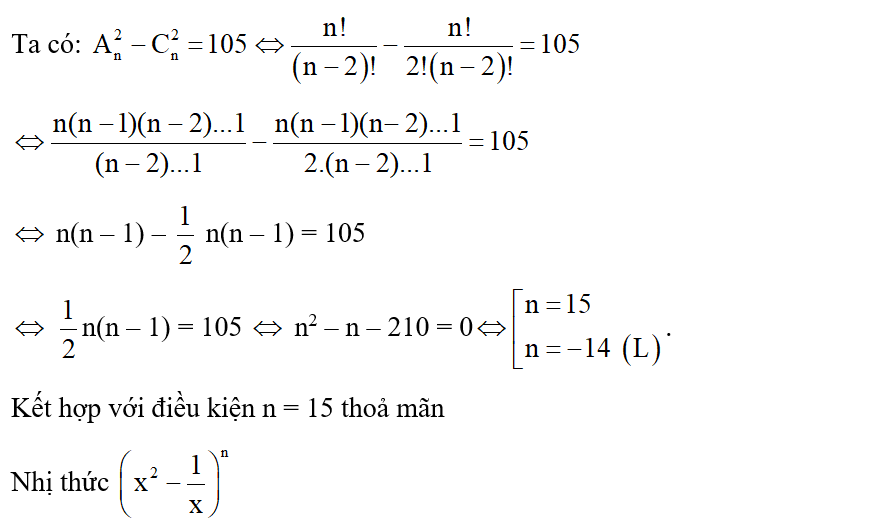

* Với khai triển (axp + bxq)n (p, q là các hằng số)
Ta có: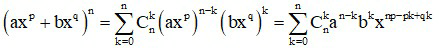
Số hạng chứa xm ứng với giá trị k thỏa mãn: np – pk + qk = m
Từ đó tìm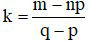
Vậy hệ số của số hạng chứa xm là: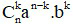
* Với khai triển P(x) = (a + bxp + cxq)n (p, q là các hằng số)
Ta có: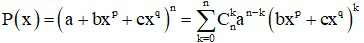
Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm.
* Chú ý:
- Nếu k không nguyên hoặc k > n thì trong khai triển không chứa xm, hệ số phải tìm bằng 0.
- Nếu hỏi hệ số không chứa x tức là tìm hệ số chứa x0.
Nhị thức Newton là một định lý toán học quan trọng liên quan đến khai triển hàm mũ của tổng và phân tích các đa thức bậc cao. Định lý Nhị thức Newton có ứng dụng rộng rãi trong toán học và nhiều lĩnh vực khác, bao gồm:
+ Tính tổ hợp và chỉnh hợp: Định lý Nhị thức Newton là công cụ quan trọng trong việc tính toán số cách sắp xếp hoặc chọn k phần tử từ n phần tử mà không quan trọng thứ tự, điều này có ứng dụng trong nhiều vấn đề tổ hợp và chỉnh hợp.
+ Dãy số: Định lý Nhị thức Newton thường được sử dụng để chứng minh các thuộc tính của các dãy số, ví dụ như dãy số Fibonacci và dãy số Pascal.
+ Xác suất và thống kê: Trong xác suất và thống kê, định lý Nhị thức Newton được sử dụng để tính xác suất và biểu diễn các phân phối xác suất, nhất là trong việc tính toán xác suất của các biến ngẫu nhiên rời rạc.
+ Lý thuyết đồ thị: Công thức Nhị thức được sử dụng để tính toán số lượng đồ thị con trong một đồ thị, điều này có ứng dụng trong lý thuyết đồ thị và các vấn đề liên quan đến mạng lưới.
2. Công thức Nhị thức Newton và khai triển
Với là những số thực tùy ý và với mọi số tự nhiên , ta có:
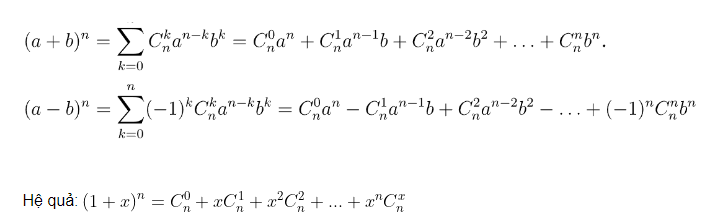
•
•
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) ứng với n = 4 và n = 5.
Chú ý:
– Các hệ số trong khai triển nhị thức Newton (a + b)n với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.
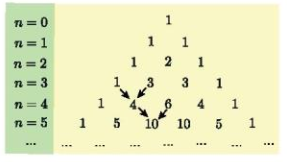
Câu 15:
22/07/2024Với n là số nguyên dương thỏa mãn , hệ số của x5 trong khai triển của biểu thức bằng
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có
n2 + n – 110 = 0
Kết hợp với điều kiện n = 10 thoả mãn bài toán.
Nhị thức
Ta có công thức số hạng tổng quát trong khai triển (a + b)n là an – k .bk (k ≤ n)
Thay a =x3, b = vào trong công thức ta có
(x3)10 – k = 2k = (2)k(x)30 – 5k
Số hạng cần tìm hệ số chứa x5 nên ta có 30 – 5k = 5
Vậy k = 5 thoả mãn bài toán
Vậy hệ số của số hạng chứa x5 trong khai triển là: (2)5 = 8064.
Có thể bạn quan tâm
- Thi Online Trắc nghiệm Toán 10 Bài 25. Nhi thức Newton có đáp án (494 lượt thi)
- Thi Online Trắc nghiệm Toán 10 KNTT Bài 25. Nhị thức Newton (Phần 2) có đáp án (756 lượt thi)
Các bài thi hot trong chương
- Thi Online Trắc nghiệm Toán 10 KNTT Bài 24. Hoán vị, tổ hợp, chỉnh hợp (Phần 2) có đáp án (754 lượt thi)
- Thi Online Trắc nghiệm Toán 10 KNTT Bài 23. Quy tắc đếm (Phần 2) có đáp án (673 lượt thi)
- Thi Online Trắc nghiệm Toán 10 KNTT Bài ôn tập cuối chương 8 (Phần 2) có đáp án (604 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 24. Hoán vị, chỉnh hợp và tổ hợp có đáp án (495 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 23. Quy tắc đếm có đáp án (396 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài tập cuối chương 8 có đáp án (373 lượt thi)