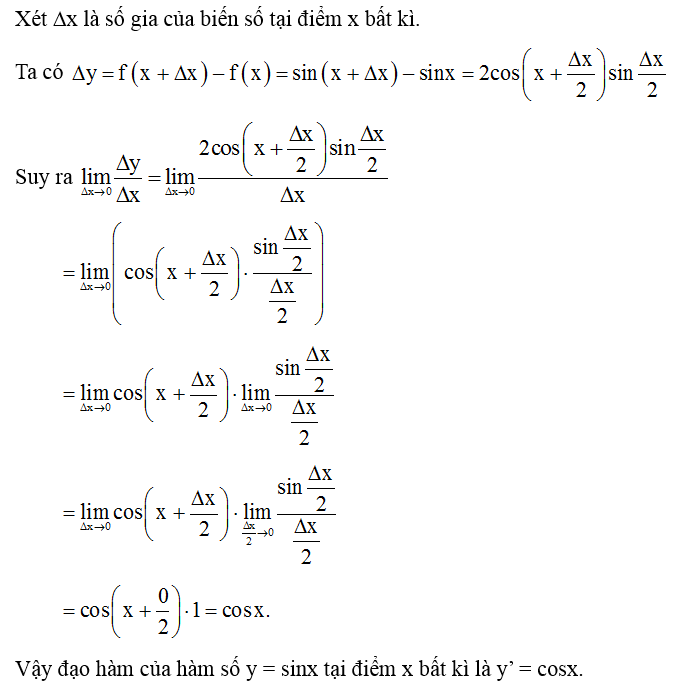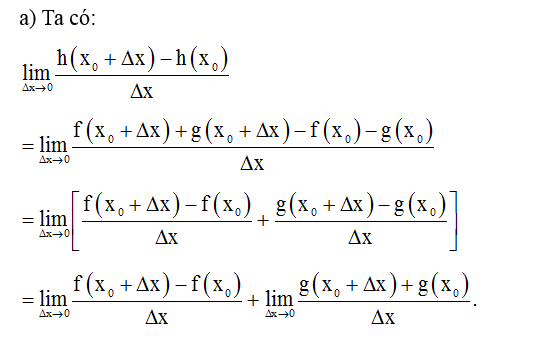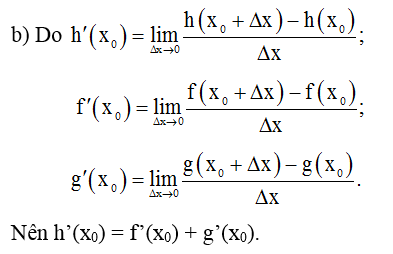45 câu hỏi trắc nghiệm thuộc Giải SGK Toán 11 CD Bài 2. Các quy tắc tính đạo hàm

Giải SGK Toán 11 CD Bài 2. Các quy tắc tính đạo hàm

Đề số 1

Giải SGK Toán 11 CD Bài 2. Các quy tắc tính đạo hàm

142 lượt thi
45 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Ta có thể tính đạo hàm của hàm số bằng cách sử dụng định nghĩa. Tuy nhiên, cách làm đó là không thuận lợi khi hàm số được cho bằng những công thức phức tạp. Trong thực tiễn, để tính đạo hàm của một hàm số ta thường sử dụng các quy tắc tính đạo hàm để đưa việc tính toán đó về tính đạo hàm của những hàm số sơ cấp cơ bản.

Đạo hàm của những hàm số sơ cấp cơ bản là gì?

Làm thế nào để thực hiện được các quy tắc đạo hàm?

Để trả lời được các câu hỏi trên, chúng ta cùng tìm hiểu bài học này.

Câu 2:

a) Tính đạo hàm của hàm số y = x² tại điểm x₀ bất kì bằng định nghĩa.

a) ⦁ Xét ∆x là số gia của biến số tại điểm x₀.

Ta có ∆y = f(x₀ + ∆x) – f(x₀) = (x₀ + ∆x)² – (x₀)²

$= x_{0}^{2} + 2 x_{0} Δ x + {(Δ x)}^{2} - x_{0}^{2}$

$= 2 x_{0} Δ x + {(Δ x)}^{2} = Δ x (2 x_{0} + Δ x) .$

Suy ra $\frac{Δ y}{Δ x} = \frac{Δ x (2 x_{0} + Δ x)}{Δ x} = 2 x_{0} + Δ x .$

⦁ Ta thấy $\lim_{Δ x \to 0} \frac{Δ y}{Δ x} = \lim_{Δ x \to 0} (2 x_{0} + Δ x) = 2 x_{0} + 0 = 2 x_{0} .$

Vậy đạo hàm của hàm số y = x² tại điểm x₀ bất kì là y’(x₀) = 2x₀.

Câu 3:

b) Dự đoán đạo hàm của hàm số y = xⁿ tại điểm x bất kì.

b) Dự đoán: y’ = nx^{n – 1}.

Câu 4:

Cho hàm số y = x²².

a) Tính đạo hàm của hàm số trên tại điểm x bất kì.

a) Ta có: y' = (x²²)' = 22x²¹.

Câu 5:

b) Tính đạo hàm của hàm số trên tại điểm x₀ = –1.

b) Đạo hàm của hàm số tại điểm x₀ = –1 là y'(–1) = 22 . (–1)²¹ = 22 . (–1) = –22.

Câu 6:

Tính đạo hàm của hàm số $y = \sqrt{x}$ tại điểm x₀ = 1 bằng định nghĩa.

Tính đạo hàm của hàm số tại điểm x0 = 1 bằng định nghĩa. (ảnh 1)

Câu 7:

Tính đạo hàm của hàm số $f (x) = \sqrt{x}$ tại điểm x₀ = 9.

Ta có: $f^{'} (x) = \frac{1}{2 \sqrt{x}}$ với x > 0.

Vậy đạo hàm của hàm số trên tại điểm x₀= 9 là $f^{'} (9) = \frac{1}{2 \sqrt{9}} = \frac{1}{2 \cdot 3} = \frac{1}{6} .$

Câu 8:

Bằng cách sử dụng kết quả $\lim_{x \to 0} \frac{\sin x}{x} = 1,$ tính đạo hàm của hàm số y = sinx tại điểm x bất kì bằng định nghĩa.

Bằng cách sử dụng kết quả lim x đến 0 sin x /x =1 tính đạo hàm của hàm số y = sinx tại điểm x bất kì bằng định nghĩa. (ảnh 1)

Câu 9:

Tính đạo hàm của hàm số f(x) = sinx tại điểm $x_{0} = \frac{π}{2} .$

Ta có f’(x) = cosx.

Đạo hàm của hàm số trên tại điểm $x_{0} = \frac{π}{2}$ là: $f^{'} (\frac{π}{2}) = \cos \frac{π}{2} = 0.$

Câu 10:

Bằng định nghĩa, tính đạo hàm của hàm số y = cosx tại điểm x bất kì.

Bằng định nghĩa, tính đạo hàm của hàm số y = cosx tại điểm x bất kì. (ảnh 1)

Câu 11:

Một vật dao động theo phương trình f(x) = cosx, trong đó x là thời gian tính theo giây. Tính vận tốc tức thời của vật tại thời điểm x₀ = 2 (s).

Ta có: f’(x) = –sinx.

Vậy vận tốc tức thời của vật tại thời điểm x₀ = 2 là: f’(2) = –sin2.

Câu 12:

Bằng định nghĩa, tính đạo hàm của hàm số y = tanx tại điểm x bất kì, $x \neq \frac{π}{2} + k π$ (k ∈ ℤ).

Bằng định nghĩa, tính đạo hàm của hàm số y = tanx tại điểm x bất kì (ảnh 1)

Câu 13:

Tính đạo hàm của hàm số f(x) = tanx tại điểm $x_{0} = - \frac{π}{6}$ .

Ta có $f^{'} (x) = \frac{1}{\cos^{2} x} (x \neq \frac{π}{2} + k π, k \in ℤ) .$

Đạo hàm của hàm số trên tại điểm $x_{0} = - \frac{π}{6}$ là: $f^{'} (- \frac{π}{6}) = \frac{1}{\cos^{2} (- \frac{π}{6})} = \frac{1}{{(\frac{\sqrt{3}}{2})}^{2}} = \frac{4}{3} .$

Câu 14:

Bằng định nghĩa, tính đạo hàm của hàm số y = cotx tại điểm x bất kì, x ≠ kπ (k ∈ ℤ).

Bằng định nghĩa, tính đạo hàm của hàm số y = cotx tại điểm x bất kì, x ≠ kπ (k ∈ ℤ). (ảnh 1)

Câu 15:

Tính đạo hàm của hàm số f(x) = cotx tại điểm $x_{0} = - \frac{π}{3} .$

Ta có: $f^{'} (x) = - \frac{1}{\sin^{2} x}$ (x ≠ kπ, k ∈ ℤ)

Đạo hàm của hàm số trên tại điểm $x_{0} = - \frac{π}{3}$ là $f^{'} (- \frac{π}{3}) = - \frac{1}{\sin^{2} (- \frac{π}{3})} = - \frac{1}{{(- \frac{\sqrt{3}}{2})}^{2}} = \frac{- 4}{3} .$

Câu 16:

Bằng cách sử dụng kết quả $\lim_{x \to 0} \frac{e^{x} - 1}{x} = 1,$ tính đạo hàm của hàm số y = e^x tại điểm x bất kì bằng định nghĩa.

Xét ∆x là số gia của biến số tại điểm x bất kì.

Ta có: ∆y = f(x + ∆x) – f(x) = e^{x + ∆x} – e^x.

Suy ra $\lim_{Δ x \to 0} \frac{Δ y}{Δ x} = \lim_{Δ x \to 0} \frac{e^{x + Δ x} - e^{x}}{Δ x} = \lim_{Δ x \to 0} \frac{e^{x} (e^{Δ x} - 1)}{Δ x} = e^{x} \lim_{Δ x \to 0} \frac{e^{Δ x} - 1}{Δ x} = e^{x} \cdot 1 = e^{x} .$

Vậy đạo hàm của hàm số y = e^x tại điểm x bất kì là y' = e^x.

Câu 17:

Tính đạo hàm của hàm số f(x) = 10^x tại điểm x₀ = –1.

Ta có f’(x) = 10^xln10

Đạo hàm của hàm số trên tại điểm x₀ =–1 là $f ’ (- 1) = 10^{- 1} \ln 10 = \frac{\ln 10}{10} .$

Câu 18:

Bằng cách sử dụng kết quả $\lim_{x \to 0} \frac{\ln (1 + x)}{x} = 1,$ tính đạo hàm của hàm số y = lnx tại điểm x dương bất kì bằng định nghĩa.

Xét ∆x là số gia của biến số tại điểm x bất kì.

Ta có: ∆y = f(x + ∆x) – f(x) = ln(x + ∆x) – lnx.

Suy ra $\lim_{Δ x \to 0} \frac{Δ y}{Δ x} = \lim_{Δ x \to 0} \frac{\ln (x + Δ x) - \ln x}{Δ x}$

$= \lim_{Δ x \to 0} \frac{\ln \frac{x + Δ x}{x}}{Δ x} = \lim_{Δ x \to 0} \frac{\ln (1 + \frac{Δ x}{x})}{Δ x}$

$= \lim_{Δ x \to 0} [\frac{1}{x} \cdot \frac{\ln (1 + \frac{Δ x}{x})}{\frac{Δ x}{x}}] = \frac{1}{x} \lim_{\frac{Δ x}{x} \to 0} \frac{\ln (1 + \frac{Δ x}{x})}{\frac{Δ x}{x}} = \frac{1}{x} .$

Vậy đạo hàm của hàm số y = lnx tại điểm x dương bất kì là $y^{'} = \frac{1}{x} .$

Câu 19:

Tính đạo hàm của hàm số f(x) = logx tại điểm $x_{0} = \frac{1}{2} .$

Ta có: $f^{'} (x) = \frac{1}{x \ln 10}$ (x > 0).

Đạo hàm của hàm số trên tại điểm $x_{0} = \frac{1}{2}$ là $f^{'} (\frac{1}{2}) = \frac{1}{\frac{1}{2} \cdot \ln 10} = \frac{2}{\ln 10} .$

Câu 20:

Cho hai hàm số f(x), g(x) xác định trên khoảng (a; b) cùng có đạo hàm tại điểm x₀ ∈ (a; b).

a) Xét hàm số h(x) = f(x) + g(x), x ∈ (a; b). So sánh:

$\lim_{Δ x \to 0} \frac{h (x_{0} + Δ x) - h (x_{0})}{Δ x}$ và $\lim_{Δ x \to 0} \frac{f (x_{0} + Δ x) - f (x_{0})}{Δ x} + \lim_{Δ x \to 0} \frac{g (x_{0} + Δ x) - g (x_{0})}{Δ x} .$

Cho hai hàm số f(x), g(x) xác định trên khoảng (a; b) cùng có đạo hàm tại điểm (ảnh 1)

Câu 21:

b) Nêu nhận xét về h'(x₀) và f'(x₀) + g’(x₀).

b) Nêu nhận xét về h'(x0) và f'(x0) + g’(x0). (ảnh 1)

Câu 22:

Tính đạo hàm của hàm số $f (x) = x \sqrt{x}$ tại điểm x dương bất kì.

Ta có $f^{'} (x) = {(x \sqrt{x})}^{'} = {(x)}^{'} \cdot \sqrt{x} + x \cdot {(\sqrt{x})}^{'}$

$= 1 \cdot \sqrt{x} + x \cdot \frac{1}{2 \sqrt{x}} = \sqrt{x} + \frac{\sqrt{x}}{2} = \frac{3 \sqrt{x}}{2}$ (x > 0).

Câu 23:

Tính đạo hàm của hàm số f(x) = tanx + cotx tại điểm $x_{0} = \frac{π}{3} .$

Xét f(x) = tanx + cotx, ta có: $f^{'} (x) = \frac{1}{\cos^{2} x} - \frac{1}{\sin^{2} x}$ với $x \neq \frac{π}{2} + k π$ và x ≠ kπ (k ∈ ℤ).

Vậy đạo hàm của hàm số trên là $f^{'} (\frac{π}{3}) = \frac{1}{\cos^{2} \frac{π}{3}} - \frac{1}{\sin^{2} \frac{π}{3}} = \frac{1}{{(\frac{1}{2})}^{2}} - \frac{1}{{(\frac{\sqrt{3}}{2})}^{2}} = 4 - \frac{4}{3} = \frac{8}{3} .$

Câu 24:

Cho hàm số y = f(u) = sinu; u = g(x) = x².

a) Bằng cách thay đổi u bởi x² trong biểu thức sinu, hãy biểu thị giá trị của u theo biến số x.

a) Ta có y = f(u) = sinu = sin(x²).

Câu 25:

b) Xác định hàm số y = f(g(x)).

b) Ta có y = f(g(x)) = f(x²) = sin(x²).

Câu 26:

Hàm số y = log₂(3x + 1) là hàm hợp của hai hàm số nào?

Đặt u = 3x + 1, ta có y = log₂u

Vậy y = log₂(3x + 1) là hàm hợp của hai hàm số y = log₂u và u = 3x + 1.

Câu 27:

Tìm đạo hàm của mỗi hàm số sau:

a) y = e^{3x + 1};

a) Đặt u = 3x + 1, ta có y = e^u.

Khi đó ${y^{'}}_{u} = {(e^{u})}^{'} = e^{u}$ và ${u^{'}}_{x} = 3.$

Theo công thức tính đạo hàm của hàm hợp, ta có: ${y^{'}}_{x} = {y^{'}}_{u} \cdot {u^{'}}_{x} = e^{u} \cdot 3 = 3 e^{u} = 3 e^{3 x + 1} .$

Câu 28:

b) y = log₃(2x – 3).

b) Đặt u = 2x – 3, ta có y = log₃u.

Khi đó ${y^{'}}_{u} = {(l o g_{3} u)}^{'} = \frac{1}{u \ln 3}$ và ${u^{'}}_{x} = 2.$

Theo công thức tính đạo hàm của hàm hợp, ta có: ${y^{'}}_{x} = {y^{'}}_{u} \cdot {u^{'}}_{x} = \frac{1}{u \ln 3} \cdot 2 = 3 = \frac{2}{u \ln 3} = \frac{2}{(2 x - 3) \ln 3} .$

Câu 29:

Cho u = u(x), v = v(x), w = w(x) là các hàm số tại điểm x thuộc khoảng xác định. Phát biểu nào sau đây là đúng?

a) (u + v + w)' = u' + v' + w';

b) (u + v – w)' = u' + v' – w';

c) (uv)' = u'v';

d) ${(\frac{u}{v})}^{'} = \frac{u^{'}}{v^{'}}$ với v = v(x) ≠ 0, v' = v'(x) ≠ 0.

Phát biểu đúng là: a), b).

Phát biểu c) sai vì (uv)' = u'v + uv'.

Phát biểu (d) sai vì ${(\frac{u}{v})}^{'} = \frac{u^{'} v - u v^{'}}{v^{2}} .$

Câu 30:

Cho u = u(x), v = v(x), w = w(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định.

Chứng minh rằng (u . v . w)' = u' . v . w + u . v' . w + u . v . w'.

Đặt g = u . v và h = g . w.

Khi đó h' = g' . w + g . w'

= (uv)' . w + (uv) . w'

= (u'v + uv') . w + (uv) . w'

= u' . v . w + u . v' . w + u . v . w'.

Câu 31:

Tìm đạo hàm của mỗi hàm số sau:

a) y = 4x³ – 3x² + 2x + 10;

a) y' = (4x³)' – (3x²)' + (2x)' + (10)'

= 4.3.x² – 3.2.x + 2.1

= 12x² – 6x + 2

Câu 32:

b) $y = \frac{x + 1}{x - 1};$

b) $y^{'} = {(\frac{x + 1}{x - 1})}^{'} = \frac{{(x + 1)}^{'} (x - 1) - (x + 1) {(x - 1)}^{'}}{{(x - 1)}^{2}}$

$= \frac{1 \cdot (x - 1) - (x + 1) \cdot 1}{{(x - 1)}^{2}} = \frac{x - 1 - x - 1}{{(x - 1)}^{2}} = \frac{- 2}{{(x - 1)}^{2}} .$

Câu 33:

c) $y = - 2 x \sqrt{x};$

c) $y^{'} = {(- 2 x \sqrt{x})}^{'} = {(- 2 x)}^{'} \cdot \sqrt{x} + (- 2 x) \cdot {(\sqrt{x})}^{'}$

$= - 2 \cdot \sqrt{x} - 2 x \cdot \frac{1}{2 \sqrt{x}} = - 2 \sqrt{x} - \sqrt{x} = - 3 \sqrt{x} .$

Câu 34:

d) y = 3sinx + 4cosx – tanx;

d) y’ = (3sinx)' + (4cosx)' – (tanx)'

$= 3 c o s x - 4 s i n x - \frac{1}{\cos^{2} x} .$

Câu 35:

e) y = 4^x + 2e^x ;

e) y' = (4^x)' + (2e^x)'

= 4^xln4 + 2e^x.

Câu 36:

g) y' = (xlnx)' = (x)'.lnx + x.(lnx)

$= 1 \cdot l n x + x \cdot \frac{1}{x} = l n x + 1.$

Câu 37:

Cho hàm số f(x) = 2^{3x + 2}.

a) Hàm số f(x) là hàm hợp của các hàm số nào?

a) Đặt y = f(x) = 2^{3x + 2} và u = 3x + 2, ta có y = 2^{3x + 2} = 2^u.

Vậy y = f(x) = 2^{3x + 2} là hàm hợp của 2 hàm số y = 2^u, u = 3x + 2.

Câu 38:

b) Tìm đạo hàm của f(x).

b) Từ y = 2^u và u = 3x + 2, ta có ${y^{'}}_{u} = {(2^{u})}^{'} = 2^{u} \ln 2$ và ${u^{'}}_{x} = 3.$

Theo công thức tính đạo hàm của hàm hợp, ta có: ${y^{'}}_{x} = {y^{'}}_{u} \cdot {u^{'}}_{x} = 2^{u} \ln 2 \cdot 3 = 3 \ln 2 \cdot 2^{u} = 3 \ln 2 \cdot 2^{3 x + 2} .$

Câu 39:

Tìm đạo hàm của mỗi hàm số sau:

a) y = sin3x + sin²x;

a) y' = (sin3x)' + (sin²x)'

= (3x)'.cos3x + 2(sinx)'.sinx

= 3.cos3x + 2cosx.sinx

= 3cos3x + sin2x.

Câu 40:

b) y = log₂(2x + 1) + 3^{−2x + 1}.

b) y' = (log₂(2x + 1))' + (3^{−2x + 1})'

$= \frac{{(2 x + 1)}^{'}}{(2 x + 1) \ln 2} + {(\frac{1}{3^{2 x - 1}})}^{'} = \frac{2}{(2 x + 1) \ln 2} - \frac{{(3^{2 x - 1})}^{'}}{{(3^{2 x - 1})}^{2}}$

$= \frac{2}{(2 x + 1) \ln 2} - \frac{{(2 x - 1)}^{'} \cdot 3^{2 x - 1} \cdot \ln 3}{{(3^{2 x - 1})}^{2}}$

$= \frac{2}{(2 x + 1) \ln 2} - \frac{2 \cdot \ln 3}{3^{2 x - 1}} = \frac{2}{(2 x + 1) \ln 2} - 2 \ln 3 \cdot 3^{- 2 x + 1} .$

Câu 41:

Viết phương trình tiếp tuyến của đồ thị mỗi hàm số sau:

a) y = x³ – 3x² + 4 tại điểm có hoành độ x₀= 2;

a) Từ y = x³ – 3x² + 4, ta có: y' = (x³)' – (3x²)' + (4)' = 3x² – 6x.

Do đó y'(2) = 3.2² – 6.2 = 12 – 12 = 0.

y(2) = 2³ – 3.2² + 4 = 8 – 12 + 4 = 0.

Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x₀ = 2 là: y = 0(x – 2) + 0 = 0.

Câu 42:

b) y = lnx tại điểm có hoành độ x₀ = e;

b) Từ y = lnx, ta có: $y^{'} = {(\ln x)}^{'} = \frac{1}{x}$

Do đó $y^{'} (e) = \frac{1}{e}$ và y(e) = lne = 1.

Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x₀ = e là: $y = \frac{1}{e} \cdot (x - e) + 1$ hay $y = \frac{1}{e} x .$

Câu 43:

c) y = e^x tại điểm có hoành độ x₀ = 0.

c) Từ y = e^x, ta có: y' = (e^x)' = e^x.

Do đó y'(0) = e⁰ = 1 và y(0) = e⁰ = 1.

Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ x₀ = 0 là: y = 1(x – 0) +1 hay y = x + 1.

Câu 44:

Một viên đạn được bắn từ mặt đất theo phương thẳng đứng với tốc độ ban đầu v₀ = 196 m/s (bỏ qua sức cản của không khí). Tìm thời điểm mà tốc độ của viên đạn bằng 0. Khi đó viên đạn cách mặt đất bao nhiêu mét (lấy g = 9,8 m/s²)?

Chọn gốc O là vị trí viên đạn được bắn lên.

Phương trình chuyển động của viên đạn là:

$y (t) = v_{0} t - \frac{1}{2} g t^{2} (g = 9, 8 m / s^{2}) .$

Vận tốc tại thời điểm t là: v = y'(t) = v₀ – gt (m/s).

Do đó để v = 0 thì v₀ – gt = 0

Suy ra $t = \frac{v_{0}}{g} = \frac{196}{9, 8} = 20 (s) .$

Khi đó, viên đạn cách mặt đất một khoảng là: $y (20) = 196 \cdot 20 - \frac{1}{2} \cdot 9, 8 \cdot 20^{2} = 1960 (m) .$

Câu 45:

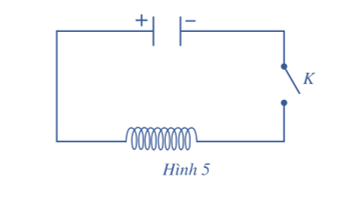
Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q₀. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức q(t) = Q₀sinωt, trong đó ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức I(t) = q'(t). Cho biết Q₀= 10^–8 (C) và ω = 10⁶π (rad/s). Tính cường độ dòng điện tại thời điểm t = 6 (s) (tính chính xác đến 10^–5 mA).

Cho mạch điện như Hình 5. Lúc đầu tụ điện có điện tích Q0. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây (ảnh 1)

I(t) = q'(t) = (Q₀sinωt)' = Q₀ω.cosωt

Cường độ của dòng điện tại thời điểm t = 6 (s) là:

I(6) = 10^–8 ∙10⁶π.cos(10⁶π.6) = 10^–2π.cos0 = 0,01π (A).

Bắt đầu thi ngay