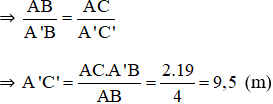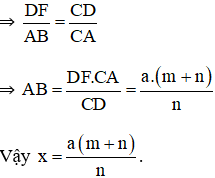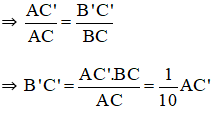Bài tập Ứng dụng thực tế của tam giác đồng dạng (có lời giải chi tiết)
-
232 lượt thi
-
3 câu hỏi
-
5 phút
Danh sách câu hỏi
Câu 1:
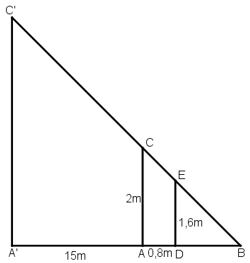
20/12/2024Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người ấy lùi ra xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?
Xem đáp án
Lời giải
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ΔA’C’B (vì AC // A’C’)
Vậy cây cao 9,5m.
*Phương pháp giải:
- Tìm ra các cặp tam giác đồng dạng phù hợp.
- Áp dụng tính chất của tam giác đồng dạng để tìm ra yêu cầu của đề bài
*Lý thuyết:
1. Định nghĩa
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
Kí hiệu: (viết theo thứ tự cặp đỉnh tương ứng).
Tỉ số là tỉ số đồng dạng của với .
Nhận xét:
- với tỉ số đồng dạng k thì với tỉ số đồng dạng . Ta nói hai tam giác A’B’C’ và ABC đồng dạng với nhau.
- Hai tam giác bằng nhau thì đồng dạng với nhau theo tỉ số đồng dạng k = 1. Mọi tam giác đồng dạng với chính nó.
- với tỉ số đồng dạng k và với tỉ số đồng dạng m thì với tỉ số đồng dạng k.m.
2. Định lí
Nếu một đường thẳng cắt hai cạnh của một tam giác là song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
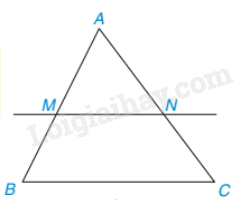
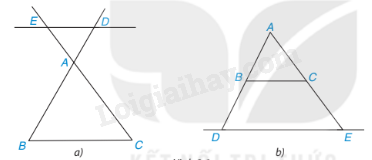
Chú ý. Định lí trên vẫn đúng nếu thay bằng đường thẳng cắt phần kéo dài của hai cạnh tam giác.
Xem thêm
Lý thuyết Hai tam giác đồng dạng – Toán lớp 8 Kết nối tri thức
Câu 2:
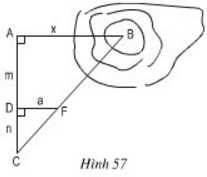
18/07/2024Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57; AB // DF; AD = m;DC = n; DF = a.
a) Em hãy nói rõ cách đo như thế nào.
b) Tính độ dài x của khoảng cách AB.
Xem đáp án
a) Cách đo:
+ Tạo một tia Ay trên mặt đất vuông góc với tia AB.
+ Trên tia Ay lấy điểm C bất kì.
+ Chọn điểm F sao cho F nằm giữa B và C.
+ Từ F hạ FD vuông góc với AC (D nằm trên AC).
+ Đo các cạnh AD, DC, DF ta tính được khoảng cách AB.
b) ΔCDF ΔCAB (do DF // AB)
Câu 3:
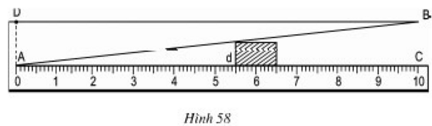
23/07/2024Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm.
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khi đó, trên thước AC ta đọc được "bề dày" d của vật (trên hình vẽ ta có có d = 5,5mm).
Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (d ≤ 10mm)
Xem đáp án
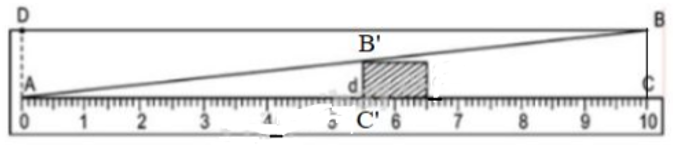
Theo hình vẽ và dựa vào định lí hai tam giác đồng dạng ta có:
ΔABC ΔAB’C’ (vì B’C’ // BC).
(Vì AC = 10cm, BC = 1cm).
Vậy khi đọc AC’ = 5,5cm thì bề dày của vật B’C’ = 5,5mm.
Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì các cạnh tương ứng tỉ lệ.