Trắc nghiệm Ứng dụng thực tế các tỉ số lượng giác của góc nhọn có đáp án (Vận dụng)
-
657 lượt thi
-
20 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Một cột đèn có bóng trên mặt đất dài 7,5m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 42o. Tính chiều cao của cột đèn. (làm tròn đến chữ số thập phân thứ ba)
Xem đáp án
Ta có chiều cao cột đèn là AC; AB = 7,5m và = 42o
Xét tam giác ACB vuông tại A có:
AC = AB. tan B = 7,5. tan 42o 6,753m
Vậy cột đèn cao 6,753m
Đáp án cần chọn là: A
Câu 2:
20/07/2024Một cầu trượt trong công việc có độ dốc là 28o và có độ cao là 2,1m. Tính độ dài của mặt cầu trượt. (làm tròn đến chữ số thập phân thứ hai)
Xem đáp án
Ta có chiều cao cột đèn là AC; AB = 6m và = 38o
Xét tam giác ACB vuông tại A có:
AC = AB. tan B = 6. tan 38o 4,68m
Vậy cột đèn cao 4,69m
Đáp án cần chọn là: B
Câu 3:
23/07/2024Một cầu trượt trong công viên có độ dốc là 28o và có độ cao là 2,1m. Tính độ dài của mặt cầu trượt. (làm tròn đến chữ số thập phân thứ hai)
Xem đáp án
Ta có độ dài của mặt cầu trượt là AB, AC = 2,1m và = 28o
Xét tam giác ACB vuông tại A có:
BC = AB : sin B = 2,1 : sin 28o 4,47m
Vậy độ dài của mặt cầu trượt là 4,47m
Đáp án cần chọn là: D
Câu 4:
21/07/2024Một cầu trượt trong công viên có độ dốc là 25o và có độ cao là 2,4m. Tính độ dài của mặt cầu trượt. (làm tròn đến chữ số thập phân thứ hai)
Xem đáp án
Ta có độ dài của mặt cầu trượt là AB, AC = 2,4m và = 25o
Xét tam giác ACB vuông tại A có:
BC = AB : sin B = 2,4 : sin 25o 5,68m
Vậy độ dài của mặt cầu trượt là 5,68m
Đáp án cần chọn là: C
Câu 7:
23/07/2024Tính chiều cao của cây trong hình vẽ bên (Làm tròn đến chữ số thập phân thứ nhất)
Xem đáp án
Chiều cao của cây là: h = 1,7 + 20. tan35o 15,7m
Đáp án cần chọn là: B
Câu 8:
08/11/2024Một cây tre cao 9m bị gió bão làm gãy ngang thân cây, ngọn cây chạm đất cách gốc 3m. Hỏi điểm gãy cách gốc bao nhiêu? (làm tròn đến chữ số thập phân thứ hai).
Xem đáp án
Đáp án đúng: C
*Lời giải:
*Phương pháp giải:
-Ta vẽ hình minh họa để dễ nhìn:
+ AB là chiều cao của cây và C là điểm dãy. Cần tính độ dài cạnh AC
+ áp dụng định lý pythagoes vào tam giác vuông ACD để tìm ra cạnh AC
* Lý thuyết nắm thêm và các công thức về tỉ số lượng giác:
Cho tam giác ABC vuông tại A (như hình vẽ).
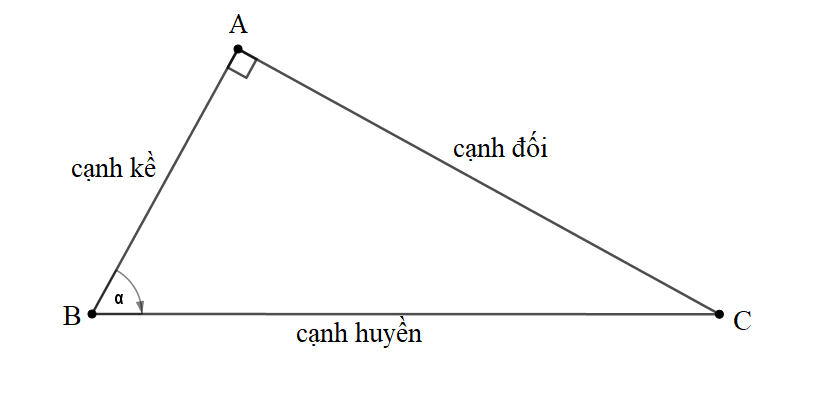
Ta có các tỉ số lượng giác của góc nhọn như sau:
Cách nhớ gợi ý: Sin đi học (đối / huyền) , Cos không hư (kề / huyền), Tan đoàn kết (đối / kề) , Cot kết đoàn (kề / đối).
Các tính chất:
(1) Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
Tức là: Cho hai góc , biết:
Khi đó, ta có:
(2) Nếu hai góc nhọn , có hoặc thì .
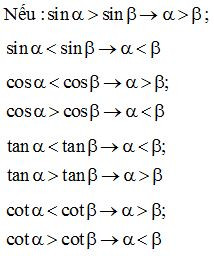
(3) Nếu là một góc nhọn bất kì thì
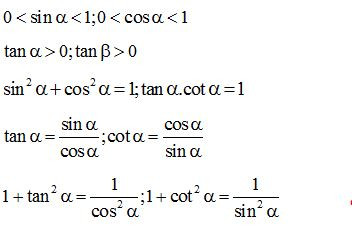
Dạng 1: Tính toán các tỉ số lượng giác, độ dài các cạnh trong tam giác
Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Dạng 2: So sánh các tỉ số lượng giác, các góc
Đưa các tỉ số lượng giác về cùng loại, áp dụng tính chất nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia và so sánh dựa trên các tính chất:
Nếu hai góc nhọn , có hoặc thì .
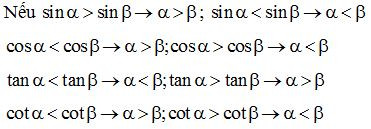
Dạng 3: Rút gọn, tính toán các biểu thức lượng giác
Áp dụng các tính chất: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia. Nếu là một góc nhọn bất kì thì:
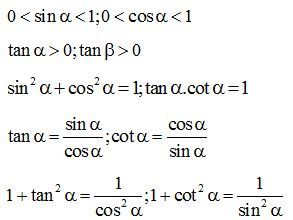
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Tỉ số lượng giác của góc nhọn (mới 2024 + Bài Tập) – Toán 9
Chuyên đề Ứng dụng thực tế các tỉ số lượng giác của góc nhọn - Toán 9
50 bài tập về Các bài toán về Tỉ số lượng giác của góc nhọn (có đáp án 2024) - Toán 9
Câu 14:
22/07/2024Một cái cây bị sét đánh trúng thân cây làm cây ngả xuống đất, tạo với mặt đất một góc là 40o. Biết rằng khúc cây còn đứng cao 1m. Tính chiều cao lúc đầu của cây.
Xem đáp án
Từ giả thiết ra có chiều dài ban đầu của cây là AD; sau khi bị sét đánh thì cây còn lại AC = 1; = 40o và CD = CB
Xét tam giác ABC vuông tại A có BC = 1,56m nên CD = 1,56m
Suy ra AD = AC + CD = 1 + 1,56 = 2,56m
Đáp án cần chọn là: D
Câu 15:
23/07/2024Một cái cây bị sét đánh trúng thân cây làm cây ngả xuống đất, tạo với mặt đất một góc là 35o. Biết rằng khúc cây còn đứng cao 1,5m. Tính chiều cao lúc đầu của cây. (làm tròn đến chữ số thập phân thứ nhất)
Xem đáp án
Từ giả thiết ra có chiều dài ban đầu của cây là AD; sau khi bị sét đánh thì cây còn lại AC = 1,5; = 35o và CD = CB
Xét tam giác ABC vuông tại A có BC = 2,6m
Suy ra AD = AC + CD = 1,5 + 2,6 = 4,1m
Vậy cây cao 4,1m
Đáp án cần chọn là: C
Câu 16:
19/07/2024Một chiếc máy bay đang bay lên với vận tốc 500km/h. Đường bay lên tạo với phương ngang một góc 30o. Hỏi sau 1,2 phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu?
Xem đáp án
Vậy máy bay đạt được độ cao là 5km sau 1,2 phút
Đáp án cần chọn là: B
Câu 17:
16/07/2024Một chiếc máy bay đang bay lên với vận tốc 480km/h. Đường bay lên tạo với phương ngang một góc 25o. Hỏi sau 1,5 phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu? (làm tròn đến chữ số thập phân thứ nhất)
Xem đáp án
Vậy máy bay đạt được độ cao là 5,1km sau 1,5 phút
Đáp án cần chọn là: C
Câu 20:
11/07/2024Bạn Thanh đứng tại vị trí A cách cây thông 6m và nhìn thấy ngọn của cây này dưới một góc bằng 55o so với phương nằm ngang (như hình vẽ). Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng 1,6m. Chiều cao BC của cây thông bằng ((làm tròn đến chữ số thập phân thứ hai)
Xem đáp án
Đặt các điểm D, E như hình vẽ.
Xét CDE vuông tại E ta có:
CE = DE. tan 55o = 6. tan 55o 8.57m
=> Chiều cao của cây là BC = CE + BE = 8,57 + 1,6 = 10,17m
Đáp án cần chọn là: D