40 câu hỏi trắc nghiệm thuộc 233 Bài trắc nghiệm Hình học Mặt nón, mặt trụ, mặt cầu có lời giải chi tiết (P1) (Đề 1)

233 Bài trắc nghiệm Hình học Mặt nón, mặt trụ, mặt cầu có lời giải chi tiết

233 Bài trắc nghiệm Hình học Mặt nón, mặt trụ, mặt cầu có lời giải chi tiết (P1) (Đề 1)

1257 lượt thi
40 câu hỏi
60 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Mệnh đề nào dưới đây là sai

A. Góc giữa hai đường sinh đối xứng qua trục của mặt nón bằng góc ở đỉnh của mặt nón

B. Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều ngoại tiếp ngoại tiếp hình nón đó, khi số cạnh đáy tăng lên vô hạn

C. Diện tích xung quanh của hình nón bằng một nửa tích của chu vi đáy với độ dài đường sinh

D. Diện tích xung quanh của hình nón tròn xoay là giới hạn của diện tích xung quanh của hình chóp đều nội tiếp hình nón đó, khi số cạnh đáy tăng lên vô hạn

Câu 2:

Gọi l, h, r lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy của hình nón. Thể tích của khối nón là

Câu 3:

Cho khối hộp trụ có thiết diện qua trục là hình vuông cạnh a. Thể tích khối trụ là:

Câu 4:

Một hình nón có tỉ lệ giữa đường sinh và bán kính đáy bằng 2. Tính góc $α$ ở đỉnh của hình nón

Câu 5:

Cho mặt cầu $S_{(O; r)}$ có diện tích đường tròn lớn là $2 π$ . Khi đó, mặt cầu $S_{(O; r)}$ có bán kính là

Câu 6:

Tính diện tích của mặt cầu có bán kính $r = 2$

Câu 7:

Thể tích khối cầu có bán kính 6cm bằng

Câu 8:

Gọi R là bán kính, S là diện tích mặt cầu và V là thể tích của khối cầu. Công thức nào sau đây sai ?

Câu 9:

Tính diện tích S của mặt cầu có đường kính bằng 6

Câu 10:

Cho khối cầu bán kính 2R. Thể tích V của khối cầu đó là

Câu 11:

Trong không gian với hệ tọa độ Oxyz, trong các mặt cầu dưới đây mặt cầu nào có bán kính R = 3?

Câu 12:

Thể tích khối cầu bán kính a bằng

Câu 13:

Thể tích khối cầu có bán kính R = 2 bằng

Đáp án đúng: C

*Lời giải:

*Phương pháp giải:

Khối cầu bán kính r có thể tích là V = $\frac{4}{3} . π . R^{3}$

* Một số lý thuyết liên quan và dạng bài toán về khối cầu:

Tính chất của mặt cầu

Nếu điểm $A$ ngoài mặt cầu $S (O; r)$ thì:

- Qua $A$ có vô số tiếp tuyến với mặt cầu.

- Độ dài các đoạn thẳng nối $A$ với các tiếp điểm đều bằng nhau.

- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.

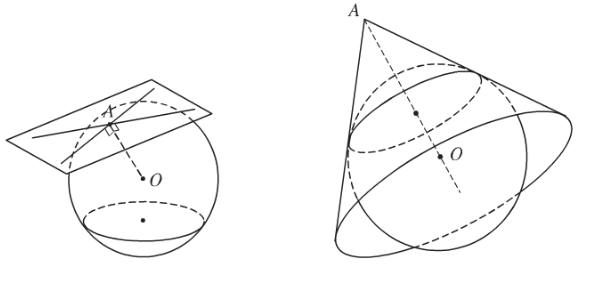
3. Vị trí tương đối của mặt cầu với đường thẳng

Cho mặt cầu $(S)$ tâm $O$ , bán kính $R$ và đường thẳng $d$ , gọi $H$ là hình chiếu của $O$ trên $d$ .

+ Nếu $O H < R$ thì $(S)$ cắt $d$ tại $2$ điểm phân biệt.

+ Nếu $O H = R$ thì $(S)$ cắt $d$ tại một điểm duy nhất $H$ . ( $d$ là tiếp tuyến với mặt cầu, $H$ là tiếp điểm)

+ Nếu $O H > R$ thì $(S)$ và $d$ không có điểm chung.

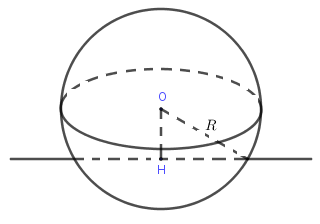
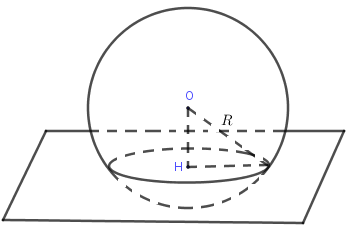
Vị trí tương đối của mặt cầu với mặt phẳng

Cho mặt cầu $(S)$ tâm $O$ , bán kính $R$ và mặt phẳng $(P)$ , gọi $H$ là hình chiếu của $O$ trên $(P)$ .

+ Nếu $O H < R$ thì $(S)$ cắt $(P)$ theo đường tròn tâm $H$ và bán kình $r = \sqrt{R^{2} - O H^{2}}$ .

+ Nếu $O H = R$ thì $(S)$ tiếp xúc $(P)$ tại tiếp điểm $H$ .

+ Nếu $O H > R$ thì $(S)$ và $(P)$ không có điểm chung.

Đặc biệt: Nếu $O H = 0 (O \equiv H)$ thì đường tròn giao tuyến của $(P)$ và $(S)$ được gọi là đường tròn lớn, $(P)$ được gọi là mặt phẳng kính.

Công thức tính diện tích mặt cầu, thể tích khối cầu

1. Công thức tính diện tích mặt cầu

- Cho mặt cầu (S) có bán kính r.

Khi đó diện tích mặt cầu $S = 4 π r^{2}$

- Chú ý: Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.

2. Công thức tính thể tích khối cầu

Khối cầu bán kính r có thể tích là V = $\frac{4}{3} . π . R^{3}$

Các dạng bài về mặt cầu và cách giải

Dạng 1. Xác định tâm và bán kính mặt cầu ngoại tiếp hình lăng trụ đứng

Ta xác định tâm O và O' của hai đáy

Tâm của mặt cầu ngoại tiếp lăng trụ lúc này chính là trung điểm của OO'

R = IA = $\sqrt{O A^{2} + O I^{2}}$

Chú ý: Hình lăng trụ nội tiếp trong một mặt cầu khi nó là hình lăng trụ đứng và có đáy đa giác nội tiếp.

Mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' có:

- Tâm là trung điểm AC'

- Bán kính R = $\frac{A C'}{2}$ = $\frac{\sqrt{a^{2} + b^{2} + c^{2}}}{2}$

Khi ABCD.A'B'C'D là hình lập phương: R = $\frac{a \sqrt{3}}{2}$

Dạng 2. Mặt cầu ngoại tiếp hình chóp

Để xác định tâm của mặt cầu ngoại tiếp hình chóp, chúng ta thực hiện theo các bước sau:

- Tìm tâm O của mặt đáy

+ Trong tam giác đều: Giao điểm của 3 đường trung tuyến

+ Hình vuông và hình chữ nhật: Giao điểm 2 đường chéo

+ Tam giác vuông: Trung điểm của cạnh huyền

- Dựng một trục d là đường thẳng đi qua O và vuông góc với đáy (d song song với chiều cao hình chóp)

- Ta sẽ xác định mặt phẳng trung trực (P) của một cạnh bên $\frac{4}{3} . π . R^{3}$

- Giao điểm của mặt phẳng (P) và d là tâm của mặt cầu ngoại tiếp

Xem thêm các bài viết liên quan hay, chi tiết:

Công thức tính diện tích mặt cầu, thể tích khối cầu (2024) chi tiết nhất

Trắc nghiệm Mặt cầu có đáp án (Vận dụng)

TOP 40 câu Trắc nghiệm Mặt cầu (có đáp án 2024) - Toán 12

Câu 14:

Thể tích của khối cầu (S) có bán kính $R = \frac{\sqrt{3}}{2}$ bằng

Câu 15:

Diện tích hình cầu bán kính $a \sqrt{3}$ là

Câu 16:

Khối cầu có bán kính R = 6 có thể tích bằng bao nhiêu?

Câu 17:

Cho mặt cầu (S) có diện tích bằng $4 π$ . Thể tích khối cầu (S) bằng

Câu 18:

Thể tích khối cầu có bán kính R bằng

Câu 19:

Diện tích xung quanh của một hình cầu bằng $16 π ({cm}^{2})$ . Bán kính của hình cầu đó là

A. 8 cm

B. 2 cm

C. 4 cm

D. 6 cm

Câu 20:

Trong không gian Oxyz, mặt cầu

$(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 y - 6 z - 11 = 0$ có bán kính bằng

A. 11

B. $\sqrt{3}$

C. 25

D. 5.

Câu 21:

Diện tích của mặt cầu bán kính $\frac{a \sqrt{3}}{2}$ bằng

Câu 22:

Cho khối trụ (T) có bán kính đáy bằng 4 và diện tích xung quanh bằng $16 π$ . Tính thể tích V của khối trụ (T)

Câu 23:

Cho hình trụ có khoảng cách giữa hai đáy bằng 10, biết diện tích xung quanh của hình trụ bằng $80 π$ . Thể tích của khối trụ là

Câu 24:

Thể tích khối cầu đường kính 2a bằng bao nhiêu

Đáp án đúng: A

*Phương pháp giải:

- Tính bán kính khối cầu

- Áp dụng công thức tính thể tích khối cầu để tính=

*Lời giải:

Bán kính khối cầu là:

R = $\frac{2 a}{2} = a$

Thể tích khối cầu là:

V = $\frac{4}{3} . π . R^{3} = \frac{4}{3} {πa}^{3}$

*Một số dạng bài và lý thuyết thêm về khối cầu:

Diện tích mặt cầu và thể tích khối cầu

Cho mặt cầu S(I; R).

Diện tích mặt cầu: $S = 4 π R^{2}$

Thể tích khối cầu: $V = \frac{4}{3} π R^{3}$

Dạng 1: Mặt cầu ngoại tiếp hình chóp

* Phương pháp giải:

- Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).

- Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục ∆ của đường tròn ngoại tiếp một đa giác của mặt bên).

- Giao điểm I của (P) và d (hoặc của ∆ và d) là tâm mặt cầu ngoại tiếp.

- Kết luận: I là tâm mặt cầu ngoại tiếp chóp.

Dạng 1.1: Hình chóp có các điểm cùng nhìn một cạnh của hình chóp dưới một góc vuông.

+) Hình chóp tam giác:

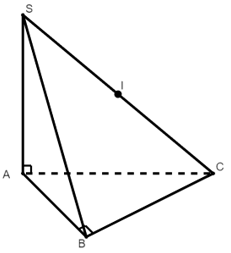
A, B cùng nhìn SC dưới một góc vuông

Tâm mặt cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SC

Bán kính là: $R = \frac{S C}{2}$

+) Hình chóp tứ giác

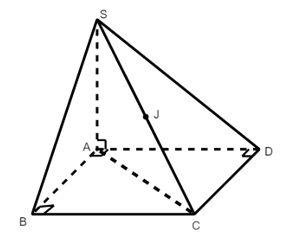
A, B, D cùng nhìn SC dưới một góc vuông

Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm J của SC

Bán kính mặt cầu là: $R = \frac{S C}{2}$

Dạng 1.2: Hình chóp có mặt bên vuông góc với mặt phẳng đáy

* Phương pháp giải: Gọi h là chiều cao hình chóp và $R_{b}, R_{d}$ là bán kính của đường tròn ngoại tiếp mặt bên, mặt đáy và $\partial$ là độ dài cạnh chung của mặt bên vuông góc với đáy thì bán kính mặt cầu là:

$R = \sqrt{{R_{b}}^{2} + {R_{d}}^{2} - {(\frac{\partial}{2})}^{2}}$

Dạng 1.3: Mặt cầu nội tiếp khối đa diện

* Phương pháp giải: Nếu đặt V là thể tích khối chóp và $S_{t p}$ là tổng diện tích mặt đáy và các mặt bên của chóp thì bán kính r của mặt cầu nội tiếp khối chóp: $r = \frac{3 V}{S_{t p}}$

Xem thêm các bài viết liên quan hay, chi tiết

Bài tập Mặt cầu Toán 12

Các bài toán thực tế hình không gian (có đáp án)

Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)

Câu 25:

Diện tích của một mặt cầu bằng $16 π ({cm}^{2})$ . Bán kính của mặt cầu đó là

A. 8 cm

B. 2 cm

C. 4 cm

D. 6 cm

Câu 26:

Diện tích của mặt cầu bán kính a bằng bao nhiêu

Câu 27:

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A (2; 4; 1)$ , $B (- 2; 2; - 3)$ . Phương trình mặt cầu đường kính AB là

Câu 28:

Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình của mặt cầu?

A. $x^{2} + y^{2} + z^{2} + 2 x - 4 y + 10 = 0$

B. $x^{2} + y^{2} + z^{2} + 2 x - 2 y - 2 z$ $- 2 = 0$

C. $x^{2} + 2 y^{2} + z^{2} + 2 x + 10 = 0$

D. $x^{2} - y^{2} + z^{2} + 2 x - 2 y - 2 z$ $- 2 = 0$

Câu 29:

Thể tích của khối cầu bán kính 3a là

Câu 30:

Mặt cầu có bán kính bằng 2a có diện tích là

Câu 31:

Tính diện tích S của mặt cầu và thể tích V của khối cầu có bán kính bằng 3cm

Câu 32:

Diện tích mặt cầu bán kính 2a là

Câu 33:

Diện tích của mặt cầu có bán kính 3m là

Câu 34:

Trong không gian với hệ tọa độ Oxyz, cho phương trình mặt cầu $(S) : {(x - 3)}^{2} + {(y + 1)}^{2} + {(z + 2)}^{2} = 8$ . Khi đó tâm I và bán kính R của mặt cầu là

Câu 35:

Tính diện tích mặt cầu có bán kính bằng 2

Câu 36:

Diện tích mặt cầu bán kính a bằng

Câu 37:

Bán kính r của khối cầu có thể tích $V = 36 π$ $(c m^{3})$ là

A. 3 cm

B. 6 cm

C. 4 cm

D. 9 cm

Câu 38:

Trong không gian Oxyz cho điểm $I (1; 2; - 1)$ và mặt phẳng $(P) : 2 x + y - 2 z + 3 = 0$ . Phương trình mặt cầu tâm I và tiếp xúc mặt phẳng (P) là

Câu 39:

Cho mặt cầu có diện tích bằng $36 {πa}^{2}$ . Thể tích khối cầu là

Câu 40:

Diện tích mặt cầu bán kính a bằng

Bắt đầu thi ngay

Bài thi liên quan