Nội dung bài viết

    Xem thêm

    Giải bài tập trang 54, 55 Chuyên đề Toán 10 Bài 7 - Kết nối tri thức

    Với Giải bài tập trang 54, 55 Chuyên đề Toán 10 trong Bài 7: Parabol sách Chuyên đề Toán lớp 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 54, 55.

    1 2,519 19/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải bài tập trang 54, 55 Chuyên đề Toán 10 Bài 7 - Kết nối tri thức

    HĐ1 trang 54 Chuyên đề Toán 10:

    Cho parabol có phương trình chính tắc y2 = 2px (H.3.18).

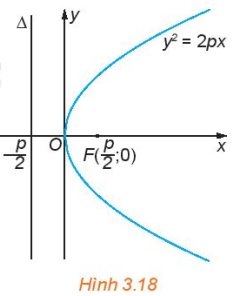
    Chuyên đề Toán 10 Bài 7: Parabol - Kết nối tri thức (ảnh 1)

    a) Nếu điểm M(x0; y0) thuộc parabol thì điểm N(x0; –y0) có thuộc parabol hay không?

    b) Từ phương trình chính tắc của parabol, có thể rút ra điều gì về hoành độ của những điểm thuộc parabol?

    Lời giải:

    a) M(x0; y0) thuộc parabol thì y02=2px0.

    Có −y02=y02=2px0 nên N(x0; –y0) cũng thuộc parabol.

    b) Từ phương trình chính tắc của parabol, ta thấy hoành độ của những điểm thuộc parabol đều không âm.

    Luyện tập 1 trang 55 Chuyên đề Toán 10:

    Trong mặt phẳng toạ độ Oxy, parabol (P) có phương trình chính tắc và đi qua điểm A(6; 6). Tìm tham số tiêu và phương trình đường chuẩn của (P).

    Lời giải:

    Gọi phương trình chính tắc của (P) là y2 = 2px (p > 0).

    Theo đề bài, (P) đi qua điểm A(6; 6) ⇒ 62 = 2p.6 ⇒ p = 3.

    Suy ra phương trình đường chuẩn của (P) là x=−32.

    HĐ2 trang 55 Chuyên đề Toán 10:

    Cho parabol có phương trình chính tắc y2 = 2px (H.3. 19).

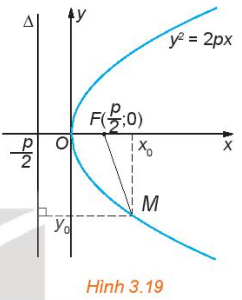
    Chuyên đề Toán 10 Bài 7: Parabol - Kết nối tri thức (ảnh 1)

    a) Nêu toạ độ tiêu điểm F và phương trình đường chuẩn Δ của parabol.

    b) Cho điểm M(x0; y0) thuộc parabol. Hãy so sánh MF với d(M; Δ), từ đó, tính MF theo x0 và y0. Độ dài MF gọi là bán kinh qua tiêu của điểm M.

    Lời giải:

    a) Điểm F có toạ độ là p2;0 và phương trình đường chuẩn là Δ:x=−p2.

    b) Theo định nghĩa parabol thì MF = d(M; Δ).

    Ta viết lại phương trình Δ: x=−p2⇔x+0.y+p2=0.

    Khoảng cách từ điểm M đến đường chuẩn Δ là:

    d(M; Δ) = x0+0.y0+p212+02=x0+p2=x0+p2.

    Vậy MF = d(M; Δ) = x0+p2.

    Luyện tập 2 trang 55 Chuyên đề Toán 10:

    Cho parabol có phương trình y2 = 8x. Tìm toạ độ tiêu điểm và phương trình đường chuẩn của parabol. Tính bán kính qua tiêu của điểm M thuộc parabol biết điểm M có tung độ bằng 4.

    Lời giải:

    Có 2p = 8 ⇒p = 4 ⇒ Toạ độ tiêu điểm là F(2; 0) và phương trình đường chuẩn của parabol là x = –2.

    Giả sử M có toạ độ là (x; 4). Khi đó ta có 42 = 8x ⇒ x = 2. Vậy M(2; 4).

    Suy ra bán kính qua tiêu của điểm M là MF = x + p2=2+42=4.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải bài tập trang 56 Chuyên đề Toán 10 Bài 7

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,519 19/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: