Nội dung bài viết

    Xem thêm

    Giải bài tập trang 44 Chuyên đề Toán 10 Bài 1 - Chân trời sáng tạo

    Với Giải bài tập trang 44 Chuyên đề Toán 10 trong Bài 1: Elip sách Chuyên đề Toán lớp 10 Chân trời sáng tạo  hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 44.

    1 1,929 20/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải bài tập trang 44 Chuyên đề Toán 10 Bài 1 - Chân trời sáng tạo

    Khám phá 2 trang 44 Chuyên đề Toán 10: Cho điểm M(x; y) nằm trên elip (E): x2a2+y2b2=1 có hai tiêu điểm là F1(–c; 0), F2(c; 0) (Hình 6).

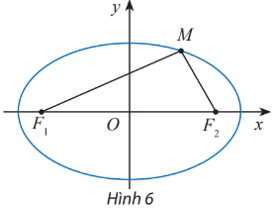
    Chuyên đề Toán 10 Bài 1: Elip - Chân trời sáng tạo (ảnh 1)

    a) Tính F1M2 và F2M2 theo x, y, c.

    b) Chứng tỏ rằng: F1M2 – F2M2 = 4cx, F1M – F2M = 2cxa.

    c) Tính độ dài hai đoạn MF1 và MF2 theo a, c, x.

    Lời giải:

    a) F1M2 = [x – (– c)]2 + (y – 0)2 = (x + c)2 + y2 = x2 + 2cx + c2 + y2;

    F2M2 = (x – c)2 + (y – 0)2 = x2 – 2cx + c2 + y2.

    b) F1M2 – F2M2 = (x2 + 2cx + c2 + y2) – (x2 – 2cx + c2 + y2) = 4cx.

    F1M2 – F2M2 = 4cx ⇒ (F1M + F2M)(F1M – F2M) = 4cx ⇒ 2a(F1M – F2M) = 4cx

    ⇒ F1M – F2M = 4cx2a = 2cxa

    c)

    +) Từ F1M + F2M = 2a và F1M−F2M=2cax ta suy ra:

    (F1M + F2M) + (F1M – F2M) = 2a + 2cax ⇒ 2F1M = 2a + 2cax ⇒ MF1 = a + x.

    +) Từ F1M + F2M = 2a và F1M−F2M=2cax ta suy ra:

    (F1M + F2M) – (F1M – F2M) = 2a – 2cax⇒  2F2M = 2a – 2cax⇒ MF2 = a – cax.

    Thực hành 2 trang 44 Chuyên đề Toán 10:

    a) Tính độ dài hai bán kính qua tiêu của điểm M(x; y) trên elip (E): x264+y236=1.

    b) Tìm các điểm trên elip (E):x2a2+y2b2=1 có độ dài hai bán kính qua tiêu bằng nhau.

    Lời giải:

    a) Có a2 = 64, b2 = 36 ⇒ a = 8, b = 6 ⇒c=a2−b2=

    Độ dài hai bán kính qua tiêu của M(x; y) là:

    MF1 = a + cax = 8 + 278x = 8 + 74x; MF2 = a – cax = 8 – 278x = 8 – 74x;

    b) Giả sử M(x; y) nằm trên (E) thoả mãn đề bài. Khi đó:

    MF1 = MF2 ⇔ 8 + 74x = 8 – 74x ⇔ x = 0 ⇔y=6y=−6.28=27.

    Vậy có hai điểm thoả mãn đề bài là M1(0; 6) và M2(0; –6).

    Vận dụng 2 trang 44 Chuyên đề Toán 10:

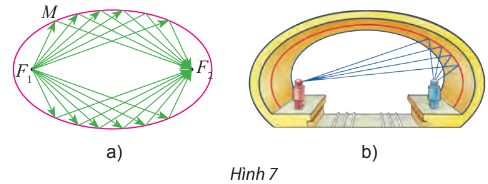
    Người ta chứng minh được rằng ánh sáng hay âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu (Hình 7a).

    Vòm xe điện ngầm của một thành phố có mặt cắt hình elip (Hình 7b). Hãy giải thích tại sao tiếng nói của một người phát ra từ một tiêu điểm bên này, mặc dù khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.

    Chuyên đề Toán 10 Bài 1: Elip - Chân trời sáng tạo (ảnh 1)

    Lời giải:

    Vì âm thanh đi từ một tiêu điểm, khi đến một điểm M bất kì trên elip luôn luôn cho tia phản xạ đi qua tiêu điểm còn lại, nghĩa là đi theo các bán kính qua tiêu nên quãng đường âm thanh đã đi là MF1 + MF2.

    Mà MF1 + MF2 = (a + cax) + (a – cax) = 2a nên quãng đường âm thanh đi luôn không đổi dù đến các điểm khác nhau trên elip, vận tốc âm thanh cũng không đổi nên thời gian âm thanh đã đi cũng không đổi. Do đó âm thanh khi đi đến các điểm khác nhau trên elip vẫn luôn dội lại tới tiêu điểm bên kia cùng một lúc.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải bài tập trang 42, 43 Chuyên đề Toán 10 Bài 1

    Giải bài tập trang 45 Chuyên đề Toán 10 Bài 1

    Giải bài tập trang 46 Chuyên đề Toán 10 Bài 1

    Giải bài tập trang 47 Chuyên đề Toán 10 Bài 1

    Giải bài tập trang 48 Chuyên đề Toán 10 Bài 1

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,929 20/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: