Nội dung bài viết

    Xem thêm

    Giải bài tập trang 24 Chuyên đề Toán 10 Bài tập cuối chuyên đề 1 - Kết nối tri thức

    Với Giải bài tập trang 24 Chuyên đề Toán 10 trong Bài tập cuối chuyên đề 1 sách Chuyên đề Toán lớp 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 24.

    1 4,698 18/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải bài tập trang 24 Chuyên đề Toán 10 Bài tập cuối chuyên đề 1 - Kết nối tri thức

    Bài 1.22 trang 24 Chuyên đề Toán 10: Cân bằng phương trình phản ứng hoá học sau

    FeS2 + O2 → Fe2O3 + SO2.

    Lời giải:

    Giả sử x, y, z, t là bốn số nguyên dương thoả mãn cân bằng phản ứng:

    xFeS2 + yO2 → zFe2O3 + tSO2.

    Vì số nguyên tử Fe, S, O ở hai vế bằng nhau nên ta có hệ:

    x=2z2x=t2y=3z+2t⇔xt=2zt2xt=12yt=3zt+2.

    Đặt X = xt, Y = yt, Z = zt ta được hệ phương trình bậc nhất ba ẩn:

    X=2Z2X=12Y=3Z+2 hay X−2Z=02X−1=02Y−3Z−2=0.

    Giải hệ này ta được X = 12, Y = 118, Z = 14 Từ đây suy ra x = 12t, y = 118t, z = 14t.

    Chọn t = 8 ta được x = 4, y = 11, z = 2. Từ đó ta được phương trình cân bằng:

    4FeS2 + 11O2 → 2Fe2O3 + 8SO2.

    Bài 1.23 trang 24 Chuyên đề Toán 10: Bạn Mai có ba lọ dung dịch chứa một loại acid. Dung dịch A chứa 10%, dung dịch B chứa 30% và dung dịch C chứa 50% acid. Bạn Mai lấy từ mỗi lọ một lượng dung dịch và hoà với nhau để có 50 g hỗn hợp chứa 32% acid này, và lượng dung dịch loại C lấy nhiều gấp đôi dung dịch loại A. Tính lượng dung dịch mỗi loại bạn Mai đã lấy.

    Lời giải:

    Gọi khối lượng dung dịch A, B, C cần lấy lần lượt là x, y, z (g).

    Theo đề bài ta có: x + y + z = 50 (1).

    – Vì dung dịch mới có nồng độ 32% nên ta có: 10%x+30%y+50%z50=32%

    ⇒10x+30y+50z=1600⇒x+3y+5z=160  2.

    – Lượng dung dịch loại C lấy nhiều gấp đôi dung dịch loại A nên z = 2x hay 2x – z = 0 (3).

    Từ (1), (2) và (3) ta có hệ phương trình: x+y+z=50x+3y+5z=1602x−z=0.

    Giải hệ này ta được x = 5, y = 35, z = 10.

    Vậy khối lượng dung dịch A, B, C cần lấy lần lượt là 5 g, 35 g, 10 g.

    Bài 1.24 trang 24 Chuyên đề Toán 10: Cho đoạn mạch như Hình 1.3. Biết R1 = 36 Ω, R2 = 45 Ω, I3 = 1,5 A là cường độ dòng điện trong mạch chinh và hiệu điện thế giữa hai đầu đoạn mạch U = 60 V. Gọi I1 và I2 là cường độ dòng điện mạch rẽ. Tính I1, I2 và R3.

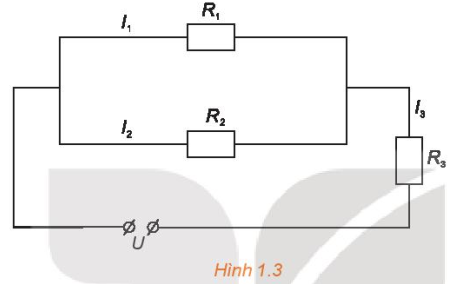
    Chuyên đề Toán 10 Bài tập cuối chuyên đề 1 - Kết nối tri thức (ảnh 1)

    Lời giải:

    Từ sơ đồ mạch điện, ta có hệ phương trình:

    I1+I2=I3R1I1+R3I3=UR1I1−R2I2=0 hay I1+I2=1,536I1+1,5R3=6036I1−45I2=0.

    Giải hệ này ta được I1=56  A, I2=23  Avà R3 = 20 V.

    Bài 1.25 trang 24 Chuyên đề Toán 10:

    Giải bài toán dân gian sau:

    Em đi chợ phiên

    Anh gửi một tiền

    Cam, thanh yên, quýt

    Không nhiều thì ít

    Mua đủ một trăm

    Cam ba đồng một

    Quýt một đồng năm

    Thanh yên tươi tốt

    Năm đồng một trái.

    Hỏi mỗi thứ mua bao nhiêu trái, biết một tiền bằng 60 đồng?

    Lời giải:

    Gọi số cam, quýt, thanh yên đã mua lần lượt là x, y, z (quả) x,y,z∈ℕ*.

    Theo đề bài, ta có hệ phương trình: 3x+y5+5z=60x+y+z=100.

    3x+y5+5z=60x+y+z=100⇔15x+y+25z=300x+y+z=100⇔15x+y+25z=300−14y+10z=−1200

    ⇔15x+y+25z=300−7y+5z=−600⇔15x+5z+6007+25z=300y=5z+6007⇔x=100−12z7y=5z+6007  *.

    Vì x > 0 nên 100 – 12z > 0 ⇒z<10012<9⇒z∈1;2;...;8.

    Thay lần lượt các giá trị này của z vào phương trình thứ hai của (*) ta thấy chỉ có z = 6 thoả mãn (vì y ∈ℕ*). Vậy z = 6, suy ra y = 90, x = 4.

    Vậy số cam, quýt, thanh yên đã mua lần lượt là 4, 90 và 6 quả.

    Bài 1.26 trang 24 Chuyên đề Toán 10: Một con ngựa giá 204 đồng (đơn vị tiền cổ). Có ba người muốn mua nhưng mỗi người không đủ tiền mua.

    Người thứ nhất nói với hai người kia: "Mỗi anh cho tôi vay một nửa số tiền của mình thì tôi đủ tiền mua ngựa";

    Người thứ hai nói: "Mỗi anh cho tôi vay một phần ba số tiền của mình, tôi sẽ mua được ngựa";

    Người thứ ba lại nói: "Chỉ cần mỗi anh cho tôi vay một phần tư số tiền của mình thì con ngựa sẽ là của tôi".

    Hỏi mỗi người có bao nhiêu tiền?

    Lời giải:

    Gọi số tiền người thứ nhất, người thứ hai, người thứ ba có lần lượt là x, y, z (đồng).

    Theo đề bài ta có:

    – Người thứ nhất nói với hai người kia: "Mỗi anh cho tôi vay một nửa số tiền của mình thì tôi đủ tiền mua ngựa", suy ra x + 12y+12z=204 (1).

    – Người thứ hai nói: "Mỗi anh cho tôi vay một phần ba số tiền của mình, tôi sẽ mua được ngựa", suy ra y+13z+13x=204 hay 13x+y+13z=204 (2).

    – Người thứ ba lại nói: "Chỉ cần mỗi anh cho tôi vay một phần tư số tiền của mình thì con ngựa sẽ là của tôi", suy ra z+14x+14y=204 hay 14x+14y+z=204 (3).

    Từ (1), (2) và (3) ta có hệ phương trình: x+12y+12z=20413x+y+13z=20414x+14y+z=204.

    Giải hệ này ta được x = 60, y = 132, z = 156.

    Vậy số tiền người thứ nhất, người thứ hai, người thứ ba có lần lượt là 60 đồng, 132 đồng, 156 đồng.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác:

    Giải bài tập trang 23 Chuyên đề Toán 10 Bài tập cuối chuyên đề 1

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 4,698 18/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: