Chuyên đề Tin học 12 Bài 16 (Kết nối tri thức): Kĩ thuật duyệt đồ thị theo chiều rộng

Giải Chuyên đề Tin học 12 Bài 16: Kĩ thuật duyệt đồ thị theo chiều rộng

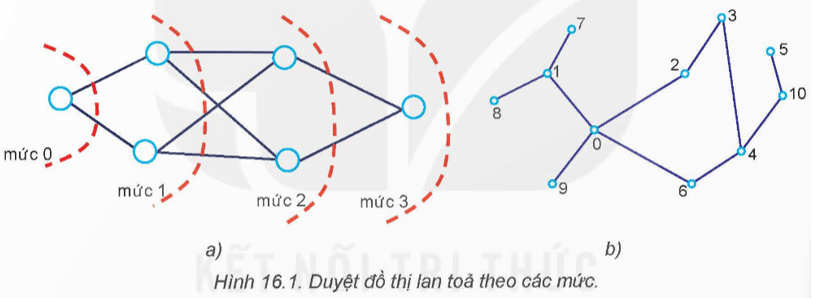
Khởi động trang 75 Chuyên đề Tin học 12: Chúng ta đã làm quen với thuật toán duyệt đồ thị theo chiều sâu, quá trình duyệt đi "sâu" nhất có thể theo các cạnh của đồ thị. Ngoài ra còn có cách duyệt đồ thị theo chiều rộng, được hình dung như khi đổ nước xuống một sàn nhà phẳng, nước sẽ lan toả ra xung quanh theo các hình tròn đồng tâm. Cách duyệt theo chiều rộng có thể được mô phỏng như Hình 16.12.

Giả sử ta bắt đầu duyệt từ đỉnh 0 của đồ thị Hình 16.1b theo chiều rộng. Theo em, chúng ta sẽ duyệt các đỉnh theo nguyên tắc nào và duyệt theo thứ tự nào?

Lời giải:

Thuật toán duyệt theo chiều rộng (BFS) bắt đầu từ một đỉnh và duyệt qua tất cả các đỉnh kề với nó trước, sau đó mới chuyển sang các đỉnh kề của các đỉnh đã duyệt. Khi duyệt từ đỉnh 0 của đồ thị Hình 16.1b, chúng ta sẽ tuân theo nguyên tắc sau:

- Nguyên tắc duyệt:

+ Duyệt tất cả các đỉnh kề với đỉnh hiện tại trước khi chuyển sang đỉnh kề tiếp theo.

+ Sử dụng hàng đợi (queue) để lưu trữ thứ tự duyệt.

- Thứ tự duyệt có thể là:

+ Bắt đầu từ đỉnh 0, thăm tất cả các đỉnh kề với đỉnh 0.

+ Sau đó, duyệt qua các đỉnh kề với các đỉnh đã thăm theo thứ tự từ hàng đợi.

+ Tiếp tục quá trình này cho đến khi tất cả các đỉnh đều được thăm.

1. Duyệt đồ thị theo chiều rộng

Hoạt động 1 trang 75 Chuyên đề Tin học 12: Thực hiện công việc duyệt theo chiều rộng của đồ thị Hình 16.1b, bắt đầu từ đỉnh 0. Các bước thực hiện sẽ duyệt các đỉnh theo trình tự sau:

- Mức 0: Bản thân đỉnh 0.

- Mức 1: Các đỉnh kề với đỉnh mức 0.

- Mức 2: Các đỉnh là kề với đỉnh mức 1. Đỉnh mức 2 là các đỉnh mà tồn tại đường đi từ đỉnh 0 đến đỉnh này theo 2 cạnh, qua đỉnh mức 1.

Quá trình cứ tiếp tục như vậy cho đến khi không thể duyệt thêm được nữa.

Trao đổi, thảo luận nhóm để nhận biết sự khác biệt giữa hai phương pháp duyệt đồ thị theo chiều sâu và chiều rộng khác nhau như thế nào.

Lời giải:

Để thực hiện duyệt theo chiều rộng (BFS) từ đỉnh 0 của đồ thị, chúng ta sẽ tuân theo các bước sau:

- Mức 0: Bắt đầu từ đỉnh 0.

- Mức 1: Duyệt tất cả các đỉnh kề với đỉnh 0.

- Mức 2: Duyệt tất cả các đỉnh kề với các đỉnh ở Mức 1 và không phải là đỉnh 0.

- Các Mức tiếp theo: Tiếp tục duyệt các đỉnh kề với đỉnh ở mức trước đó, không lặp lại các đỉnh đã duyệt.

Quá trình này tiếp tục cho đến khi tất cả các đỉnh có thể tiếp cận từ đỉnh 0 đều được duyệt.

Sự khác biệt chính giữa hai phương pháp duyệt đồ thị theo chiều sâu (DFS) và chiều rộng (BFS) là:

- DFS: Duyệt sâu vào từng nhánh của đồ thị trước khi quay lại (backtrack).

- BFS: Duyệt đồ thị theo từng mức độ rộng, từ gần đến xa so với điểm bắt đầu.

Câu hỏi 1 trang 76 Chuyên đề Tin học 12: Mệnh đề sau đúng hay sai?

Giả sử gọi BFS(Adj,s) là chương trình duyệt đồ thị theo chiều rộng bắt đầu từ đỉnh s. Khi đó với mọi đỉnh v thuộc V, hàm BFS(Adj,s) sẽ duyệt qua đỉnh v khi và chỉ khi tồn tại đường đi từ s đến v.

Lời giải:

Mệnh đề sau là đúng.

- Lý do:

Mệnh đề này có thể được chứng minh tương tự như cách chứng minh tính chất của DFS đối với đường đi trong đồ thị. Cụ thể:

- Chứng minh:

Chúng ta cần chứng minh hai điều sau:

1. Nếu tồn tại đường đi từ đỉnh sss đến đỉnh v, thì quá trình duyệt BFS từ đỉnh sss sẽ duyệt qua đỉnh v.

2. Nếu quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v, thì tồn tại đường đi từ đỉnh sss đến đỉnh v.

- Chứng minh điều 1:

Nếu tồn tại đường đi từ đỉnh s đến đỉnh v:

- Giả sử tồn tại một đường đi từ đỉnh sss đến đỉnhv. Điều này có nghĩa là có một dãy các đỉnh s=v0,v1,v2,…,vk sao cho (vi,vi+1) ∈ E

- Khi thực hiện BFS từ đỉnh sss, BFS sẽ thăm tất cả các đỉnh mà nó có thể truy cập được từ sss. BFS duyệt các đỉnh theo từng mức (level) một cách rộng nhất có thể trước khi chuyển sang mức tiếp theo.

- Điều này bao gồm các đỉnh v1,v2,…,vk vì chúng liên tiếp nhau trong đường đi từ s đến v.

- Do đó, nếu tồn tại đường đi từ đỉnh s đến đỉnh v, BFS sẽ chắc chắn thăm đỉnh v trong quá trình duyệt.

- Chứng minh điều 2:

Nếu quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v:

- Giả sử quá trình duyệt BFS từ đỉnh sss duyệt qua đỉnh v. Điều này có nghĩa là BFS đã bắt đầu từ đỉnh sss và theo các cạnh của đồ thị, nó đã đến đỉnh v.

- BFS duyệt đồ thị bằng cách đi theo các cạnh của đồ thị, nên mỗi bước từ đỉnh hiện tại đến đỉnh tiếp theo trong quá trình duyệt BFS đều là di chuyển qua các cạnh của đồ thị.

- Nếu BFS đã thăm đỉnh v từ đỉnh s, điều đó có nghĩa là có một dãy các đỉnh bắt đầu từ sss và kết thúc tại v sao cho mỗi đỉnh trong dãy này đều có cạnh nối với đỉnh tiếp theo trong dãy.

- Do đó, tồn tại một đường đi từ đỉnh s đến đỉnh v.

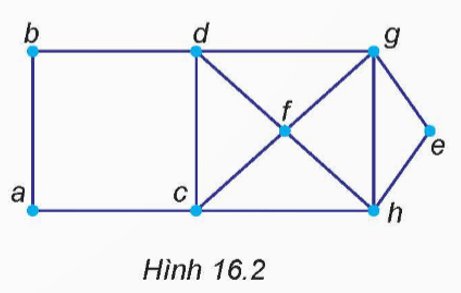
Câu hỏi 2 trang 76 Chuyên đề Tin học 12: Trả lời các câu hỏi dựa trên đồ thị Hình 16.2.

a) Các đỉnh kề với a là đỉnh nào?

b) Khoảng cách từ đỉnh a đến e là bao nhiêu?

c) Nếu thực hiện duyệt đồ thị theo chiều rộng bắt đầu từ đỉnh a thì thứ tự các đỉnh được duyệt có thể như thế nào?

Lời giải:

a) Các đỉnh kề với a:

Đỉnh ‘b’, ‘c’ là các đỉnh kề với đỉnh ‘a’.

b) Khoảng cách từ a đến e:

Khoảng cách ngắn nhất từ đỉnh ‘a’ đến đỉnh ‘e’ là ba cạnh, thông qua đỉnh ‘c’ và ‘h’.

c) Thứ tự duyệt đồ thị theo chiều rộng từ a:

Một thứ tự có thể là: a, b, c, d, f, g, e, h.

Hoạt động 2 trang 77 Chuyên đề Tin học 12: Tìm hiểu, thảo luận về cách cài đặt thuật toán theo chiều rộng.

Lời giải:

Thuật toán duyệt theo chiều rộng (Breadth-First Search, BFS) là một thuật toán duyệt hoặc tìm kiếm trên cây hoặc đồ thị. BFS bắt đầu từ một đỉnh gốc và khám phá các đỉnh lân cận trước khi di chuyển đến các đỉnh xa hơn. Đây là một phương pháp duyệt theo tầng (level-order traversal).

Cài đặt thuật toán BFS

Để cài đặt BFS, chúng ta cần sử dụng một hàng đợi (queue) để theo dõi các đỉnh sẽ được thăm tiếp theo. Hàng đợi đảm bảo rằng các đỉnh được thăm theo thứ tự mà chúng được khám phá.

Dưới đây là các bước cơ bản để cài đặt BFS:

- Khởi tạo hàng đợi: Đẩy đỉnh bắt đầu vào hàng đợi và đánh dấu nó đã được thăm.

- Duyệt đỉnh: Lặp lại quá trình sau cho đến khi hàng đợi rỗng:

+ Lấy đỉnh ở đầu hàng đợi ra.

+ Duyệt tất cả các đỉnh kề của đỉnh này. Nếu một đỉnh kề chưa được thăm, đánh dấu nó đã được thăm và đẩy nó vào hàng đợi.

Câu hỏi 1 trang 79 Chuyên đề Tin học 12: Thứ tự các đỉnh có trong danh sách đỉnh kề Adj có ảnh hưởng đến thứ tự các đỉnh được đánh dấu trong thuật toán duyệt theo chiều rộng hay không?

Lời giải:

Thứ tự các đỉnh có trong danh sách đỉnh kề (Adjacency List) có ảnh hưởng đến thứ tự các đỉnh được đánh dấu trong thuật toán duyệt theo chiều rộng (BFS).

Ảnh hưởng của thứ tự đỉnh trong danh sách đỉnh kề:

1. Thứ tự duyệt các đỉnh gần gốc trước: Nếu đỉnh gốc nằm ở đầu danh sách đỉnh kề, các đỉnh gần gốc sẽ được duyệt trước. Điều này có thể dẫn đến việc duyệt đồ thị theo một hướng cụ thể và có thể tạo ra kết quả khác nhau nếu thứ tự này được thay đổi.

2. Thứ tự duyệt các đỉnh xa gốc sau: Các đỉnh ở phía sau trong danh sách sẽ được duyệt sau. Do đó, các đỉnh xa gốc sẽ được duyệt sau khi đã duyệt qua các đỉnh gần gốc.

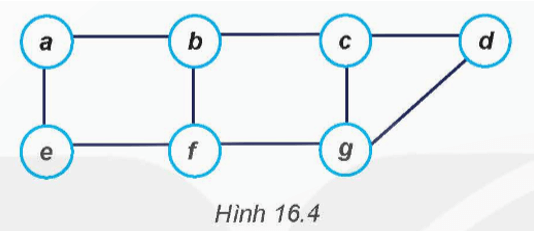
Câu hỏi 2 trang 79 Chuyên đề Tin học 12: Cho đồ thị Hình 16.4. Nếu thực hiện duyệt theo chiều sâu và chiều rộng bắt đầu từ đỉnh a thì thứ tự các đỉnh được duyệt sẽ như thế nào?

Lời giải:

Thứ tự các đỉnh được duyệt khi thực hiện duyệt theo chiều sâu (DFS) và chiều rộng (BFS) bắt đầu từ đỉnh ‘a’:

Duyệt theo chiều sâu (DFS):

- Thứ tự có thể là: a, b, c, d, c, g, b, a, e, f.

Duyệt theo chiều rộng (BFS):

- Thứ tự có thể là: a, b, e, c, f, g, d.

Luyện tập 1 trang 79 Chuyên đề Tin học 12: Viết lại hàm BFS() in ra các đỉnh đã duyệt. Áp dụng vào đồ thị trong bài để kiểm tra thứ tự các đỉnh đã duyệt có đúng như phần mô phỏng thủ công các hoạt động trên không.

Lời giải:

Gợi ý viết tổng quát của hàm BFS sử dụng ma trận kề của đồ thị:

from collections import deque

def BFS(matrix, start):

n = len(matrix) # Số lượng đỉnh trong đồ thị

visited = set() # Sử dụng một set để lưu trữ các đỉnh đã được duyệt

queue = deque([start]) # Khởi tạo hàng đợi và thêm đỉnh bắt đầu vào đó

while queue:

vertex = queue.popleft() # Lấy đỉnh ở đầu hàng đợi ra

if vertex not in visited:

print("Visit:", vertex) # In ra đỉnh đã duyệt

visited.add(vertex) # Đánh dấu đỉnh đã duyệt

for neighbor in range(n): # Duyệt qua tất cả các đỉnh

if matrix[vertex][neighbor] == 1 and neighbor not in visited:

queue.append(neighbor) # Thêm các đỉnh kề chưa được duyệt vào hàng đợi

# Đồ thị mẫu dưới dạng ma trận kề

graph_matrix = [

[0, 1, 1, 0, 0, 0], # A

[1, 0, 0, 1, 1, 0], # B

[1, 0, 0, 0, 0, 1], # C

[0, 1, 0, 0, 0, 0], # D

[0, 1, 0, 0, 0, 1], # E

[0, 0, 1, 0, 1, 0] # F

]

# Thực hiện BFS từ đỉnh 0 (tương ứng với đỉnh 'A')

BFS(graph_matrix, 0)

- Chú ý: Trong hàm BFS này, ta sử dụng ma trận kề matrix để xác định các đỉnh kề của mỗi đỉnh. Nếu một đỉnh kề chưa được duyệt, ta thêm nó vào hàng đợi để duyệt tiếp. Quá trình này được lặp lại cho tất cả các đỉnh kề của mỗi đỉnh được duyệt.

Luyện tập 2 trang 79 Chuyên đề Tin học 12: Viết lại hàm BFS() duyệt theo chiều rộng nhưng sử dụng dữ liệu là ma trận kề A của đồ thị.

Lời giải:

Gợi ý viết tổng quát của hàm BFS sử dụng ma trận kề của đồ thị:

from collections import deque

def BFS(matrix, start):

n = len(matrix) # Số lượng đỉnh trong đồ thị

visited = set() # Sử dụng một set để lưu trữ các đỉnh đã được duyệt

queue = deque([start]) # Khởi tạo hàng đợi và thêm đỉnh bắt đầu vào đó

while queue:

vertex = queue.popleft() # Lấy đỉnh ở đầu hàng đợi ra

if vertex not in visited:

print("Visit:", vertex) # In ra đỉnh đã duyệt

visited.add(vertex) # Đánh dấu đỉnh đã duyệt

for neighbor in range(n): # Duyệt qua tất cả các đỉnh

if matrix[vertex][neighbor] == 1 and neighbor not in visited:

queue.append(neighbor) # Thêm các đỉnh kề chưa được duyệt vào hàng đợi

# Đồ thị mẫu dưới dạng ma trận kề

graph_matrix = [

[0, 1, 1, 0, 0, 0], # A

[1, 0, 0, 1, 1, 0], # B

[1, 0, 0, 0, 0, 1], # C

[0, 1, 0, 0, 0, 0], # D

[0, 1, 0, 0, 0, 1], # E

[0, 0, 1, 0, 1, 0] # F

]

# Thực hiện BFS từ đỉnh 0 (tương ứng với đỉnh 'A')

BFS(graph_matrix, 0)

- Chú ý: Trong hàm BFS này, ta sử dụng ma trận kề matrix để xác định các đỉnh kề của mỗi đỉnh. Nếu một đỉnh kề chưa được duyệt, ta thêm nó vào hàng đợi để duyệt tiếp. Quá trình này được lặp lại cho tất cả các đỉnh kề của mỗi đỉnh được duyệt.

Vận dụng 1 trang 79 Chuyên đề Tin học 12: Cho đơn đồ thị vô hướng G = (V, E). Sử dụng thuật toán duyệt theo chiều rộng BFS, viết chương trình kiểm tra xem G có chu trình hay không. Chu trình (cycle) ở đây được hiểu là một đường đi khép kín, đỉnh xuất phát trùng với đỉnh kết thúc. Cần thiết lập hàm dạng Acycle(G), hàm trả lại True nếu G không có chu trình, ngược lại hàm trả lại False.

Lời giải:

Để kiểm tra xem đồ thị có chu trình hay không, ta có thể sử dụng thuật toán BFS để duyệt đồ thị và kiểm tra xem có đỉnh nào được duyệt lại không. Nếu có đỉnh nào đã được duyệt và nó là đỉnh kề của đỉnh hiện tại, thì đồ thị chứa chu trình.

Dưới đây là một cài đặt Python cho hàm Acycle(G):

from collections import deque

def Acycle(G):

# Hàm kiểm tra có chu trình hay không

def has_cycle(graph, start):

visited = set()

queue = deque([(start, None)]) # Lưu trữ cả cạnh đến đỉnh đang duyệt

while queue:

vertex, parent = queue.popleft()

visited.add(vertex)

for neighbor in graph[vertex]:

if neighbor != parent: # Loại bỏ trường hợp quay lại đỉnh cha

if neighbor in visited:

return True # Đồ thị có chu trình

else:

queue.append((neighbor, vertex)) # Thêm đỉnh kề vào hàng đợi

return False # Đồ thị không có chu trình

# Duyệt qua tất cả các đỉnh của đồ thị

for vertex in G:

if has_cycle(G, vertex):

return False # Nếu có chu trình, trả về False

return True # Nếu không có chu trình, trả về True

# Ví dụ về đồ thị được biểu diễn bằng danh sách kề

graph = {

'A': ['B', 'C'],

'B': ['A', 'D', 'E'],

'C': ['A', 'F'],

'D': ['B'],

'E': ['B', 'F'],

'F': ['C', 'E']

}

# Kiểm tra đồ thị có chu trình hay không

print(Acycle(graph)) # False

- Chú ý: Trong hàm Acycle(G), ta duyệt qua tất cả các đỉnh của đồ thị và sử dụng hàm has_cycle(graph, start) để kiểm tra xem có chu trình bắt đầu từ đỉnh đó hay không. Nếu ta tìm thấy bất kỳ chu trình nào, ta trả về False. Nếu không có chu trình nào được tìm thấy, ta trả về True.

Vận dụng 2 trang 79 Chuyên đề Tin học 12: Cho đơn đô thị G = (V, E) vô hướng hoặc có hướng. Cho trước hai đỉnh bất kì s và t. Viết chương trình kiểm tra xem có tồn tại đường đi từ s đến thay không. Nếu có thì chương trình cần chỉ ra dãy các đỉnh tương ứng trên đường đi từ s đến t, nói cách khác chương trình cần chỉ ra một dãy các đỉnh Vo, V1,..., Vk sao cho:

(Vj-1, Vj) là cạnh của đô thị với j = 1, 2, ..., k;

s = Vo, t = Vk

Lời giải:

Cài đặt Python cho chương trình kiểm tra xem có tồn tại đường đi từ đỉnh sss đến ttt, và nếu có, nó sẽ trả về dãy các đỉnh trên đường đi từ s đến t:

from collections import deque

def find_path(graph, start, end):

# Hàm duyệt đồ thị để tìm đường đi từ start đến end

def BFS(graph, start, end):

visited = set()

queue = deque([(start, [start])]) # Lưu trữ đường đi từ start đến đỉnh đang xét

while queue:

vertex, path = queue.popleft()

visited.add(vertex)

if vertex == end:

return path # Trả về đường đi nếu tìm thấy đỉnh kết thúc

for neighbor in graph[vertex]:

if neighbor not in visited:

queue.append((neighbor, path + [neighbor])) # Thêm đỉnh kề vào hàng đợi với đường đi mới

return None # Trả về None nếu không tìm thấy đường đi

# Kiểm tra xem có đường đi từ start đến end không

path = BFS(graph, start, end)

return path

# Ví dụ về đồ thị được biểu diễn bằng danh sách kề

graph = {

'A': ['B', 'C'],

'B': ['A', 'D', 'E'],

'C': ['A', 'F'],

'D': ['B'],

'E': ['B', 'F'],

'F': ['C', 'E']

}

start = 'A'

end = ‘F’

# Kiểm tra xem có tồn tại đường đi từ start đến end không

path = find_path(graph, start, end)

if path:

print("Đường đi từ", start, "đến", end, "là:", " -> ".join(path))

else:

print("Không tồn tại đường đi từ", start, "đến", end)

- Chú ý: Trong chương trình này, chúng ta sử dụng thuật toán BFS để duyệt đồ thị và tìm đường đi từ đỉnh sss đến ttt. Nếu đường đi được tìm thấy, chúng ta trả về dãy các đỉnh trên đường đi. Nếu không có đường đi, chúng ta trả về None.