Chuyên đề Tin học 12 Bài 15 (Kết nối tri thức): Kiểm định giả thuyết thống kê

Giải Chuyên đề Tin học 12 Bài 15: Kiểm định giả thuyết thống kê

Khởi động trang 86 Chuyên đề Tin học 12: Giả sử, trong những nghiên cứu thống kê trước đây với quy mô cả nước, người ta đã tính được chỉ số thông minh (IQ) trung bình của học sinh lớp 12 là 100. Năm nay, khảo sát ngẫu nhiên chỉ số này của 100 học sinh lớp 12 và từ số liệu khảo sát tính được trung bình IQ là 110. Liệu chỉ số IQ của học sinh lớp 12 có tăng lên so với trước? Phương pháp thống kê nào trả lời được câu hỏi này?

Lời giải:

Giả sử, trong những nghiên cứu thống kê trước đây với quy mô cả nước, người ta đã tính được chỉ số thông minh (IQ) trung bình của học sinh lớp 12 là 100. Năm nay, khảo sát ngẫu nhiên chỉ số này của 100 học sinh lớp 12 và từ số liệu khảo sát tính được trung bình IQ là 110. Giả sử chỉ số IQ của học sinh lớp 12 có tăng lên so với trước. Phương pháp kiểm định và giả thiết thống kê nào trả lời được giả sử trên là đúng hay sai.

1. Bài toán kiểm định giả thuyết thống kê

Hoạt động 1 trang 86 Chuyên đề Tin học 12: Xác định các giả thuyết của bài toán kiểm định một giá trị trung bình.

Hãy cùng thảo luận và xác định giả thuyết gốc H₀, giả thuyết thay thế H₁ của bì toán nêu trong phần khởi động.

Lời giải:

Bài toán kiểm định một trung bình lựa chọn các giả thuyết sau:

- Giả thuyết gốc H₀: u=u₀ “giá trị trung bình (u) của tổng thể bằng u₀ cho trước”. Giá trị u₀ thường được xác định trước từ thông tin ngoài dữ liệu quan sát. Chẳng hạn với tình huống nêu trong phần khởi động, u là giá trị IQ trung bình của học sinh lớp 12 cả nước năm nay (năm quan sát) mà chúng ta chưa biết và có thể cho rằng giá trị này bằng IQ trung bình của học sinh lớp 12 các năm trước, u₀ = 100. Giả thuyết gốc Họ có thể viết ngắn gọn là H₀- u = 100.

- Giả thuyết thay thế H₀: “Giá trị u nhỏ hơn hoặc lớn hơn u₀” (kiểm định một phía) hoặc “Giá trị u khác u₀” (kiểm định hai phía). Trường hợp kiểm định một phía có thể viết gọn là H₁: u > u₀ hoặc H₁: u < u₀; với trường hợp kiểm định hai phía H₁: u # u₀

- Giả thuyết thay thế H₁ nói chung là một trong các giả thuyết khác giả thuyết gốc. Giả thuyết này có thể phát sinh từ dữ liệu hay các thông tin khác. Chẳng hạn, với tình huống nêu trong phần khởi động, giả thiết thay thế là H₁: u > u₀ (hay u > 100), vì theo số liệu quan sát IQ của 100 học sinh ta có trung bình mẫu số liệu là 110 (lớn hơn 100).

Hoạt động 2 trang 87 Chuyên đề Tin học 12: Khối lượng của trẻ 36 tháng tuổi là đại lượng ngẫu nhiên phân phối chuẩn. Do các điều kiện khác nhau ở hai thành phố A và B, người ta muốn so sánh khối lượng trung bình của trẻ 36 tháng tuổi ở hai thành phố này. Gọi H, I, là trọng lượng trung bình của trẻ độ tuổi này ở hai thành phố A và B. Em hãy chọn giả thuyết gốc và giả thuyết thay thế để kết luận về vấn đề trên trong trường hợp:

a) Chưa có số liệu về khối lượng của trẻ 36 tháng tuổi ở các thành phố A và B.

b) Có số liệu thu thập về khối lượng của các trẻ độ tuổi này của 50 trẻ ở mỗi thành phố trên và tính được khối lượng trung bình của 50 trẻ ở thành phố A là 14.2 kg, 50 trẻ ở thành phố B là 14.5 kg.

Lời giải:

Câu hỏi 1 trang 88 Chuyên đề Tin học 12: Em sẽ chọn giả thuyết H1 nào cho kiểm định 1 phía với H1: u > u0 khi trung bình số liệu mẫu lớn hơn u0?

Lời giải:

Chúng ta có thông tin từ số liệu mẫu ở các thành phố A và B. Đó là cơ sở chọn H₁: u₁ > u_2. Đây là bài toán kiểm định một phía.

Câu hỏi 2 trang 88 Chuyên đề Tin học 12: Khi kiểm định giả thuyết 1 trung bình bằng Z.TEST, giá trị trả về của hàm Z.TEST là 0.04. Với mức ý nghĩa 5%, em có bác bỏ giả thuyết gốc hay không?

Lời giải:

Khi kiểm định giả thuyết 1 trung bình bằng Z.TEST, giá trị trả về của hàm Z.TEST là 0.04. Với mức ý nghĩa 5%, em không bác bỏ giả thuyết gốc.

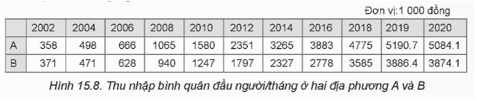
Luyện tập trang 91 Chuyên đề Tin học 12: Hình 15.8 cho số liệu mẫu thu nhập bình quân đầu người /tháng của hai địa phương A và B. Thu nhập bình quân đầu người /tháng ở A và B khác nhau, đúng hay sai?

Lời giải:

Hình 15.8 cho số liệu mẫu thu nhập bình quân đầu người/tháng của hai địa phương A và B. Thu nhập bình quân đầu người/tháng ở A và B khác nhau là đúng vì thu nhập theo từng năm khác nhau.

Vận dụng trang 91 Chuyên đề Tin học 12: Thời gian ngủ trung bình/ngày của trẻ 3 tuổi được khuyến cáo là 13 giờ. Bảng sau cho số liệu quan sát số giờ ngủ/ngày của 20 trẻ ở địa phương A:

Hãy cho biết với mức ý nghĩa 5% có thể cho rằng trẻ 3 tuổi ở địa phương A có số giờ ngủ/ngày khác với khuyến cáo trên hay không.

Lời giải:

Trung bình mẫu: =AVERAGE(D2:W2) cho kết quả là: 11.9

=Z.TEST(D2:W2,13) cho kết quả là: 0.999

=MIN(0.05,1-0.05) cho kết quả là: 0.05

Kết quả cho thấy so sánh giá trị của Z.TEST là 0.999 với giá trị 0.05, kết luận bác bỏ H₁, chấp nhận H₀, tức là với ý nghĩa của 5% không thể xác nhận rằng trẻ 3 tuổi ở địa phương A có số giờ ngủ/ngày khác với khuyến cáo trên.