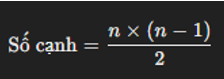Chuyên đề Tin học 12 Bài 12 (Kết nối tri thức): Biểu diễn đồ thị

Giải Chuyên đề Tin học 12 Bài 12: Biểu diễn đồ thị

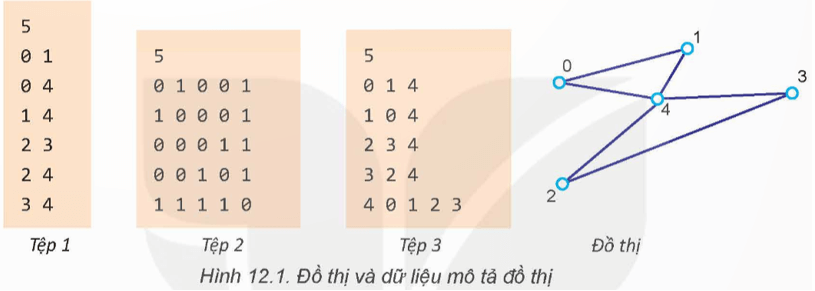
Khởi động trang 56 Chuyên đề Tin học 12: Quan sát đồ thị Hình 12.1 và cho biết mỗi tệp dữ liệu sau có ý nghĩa gì?

Lời giải:

Ý nghĩa của Tệp 1, Tệp 2, Tệp 3:

Tệp 1: Có vẻ như đại diện cho một ma trận kết nối, với các hàng tương ứng với các điểm và cột chỉ ra sự liên kết giữa chúng.

Tệp 2: Có thể biểu diễn các trạng thái hoặc thuộc tính của các điểm trong mạng lưới, với mỗi hàng biểu thị một trạng thái khác nhau.

Tệp 3: Có khả năng là một biểu đồ của các sự kiện hoặc tương tác giữa các điểm, với các số liệu thể hiện mức độ hoặc cường độ của tương tác.

Đồ thị “Đồ thị” bên cạnh các tệp dữ liệu cho thấy mối quan hệ giữa các điểm được biểu diễn bằng các đường nối, tạo ra một cấu trúc mạng hoặc như một mạng nhện. Điều này giúp ta hình dung được cách thức mà dữ liệu số có thể được trực quan hóa thành các mối quan hệ phức tạp.

1. Mô hình dữ liệu đồ thị

Hoạt động 1 trang 56 Chuyên đề Tin học 12: Tìm hiểu, thảo luận về các cách biểu diễn dữ liệu của một đồ thị G.

Lời giải:

Có nhiều cách để biểu diễn dữ liệu của một đồ thị GGG, mỗi cách có những ưu điểm và hạn chế riêng. Dưới đây là một số cách phổ biến để biểu diễn đồ thị:

- Danh sách cạnh (Edge List)

- Danh sách kề (Adjacency List)

- Ma trận kề (Adjacency Matrix)

- Danh sách kề và trọng số (Weighted Adjacency List), như đồ thị đường đi ngắn nhất.

- Ma trận trọng số (Weighted Adjacency Matrix)

Mỗi cách biểu diễn có ưu điểm và hạn chế riêng, và việc lựa chọn phụ thuộc vào mục đích cụ thể của việc sử dụng dữ liệu đồ thị.

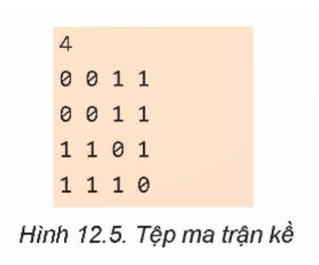
Câu hỏi 1 trang 57 Chuyên đề Tin học 12: Vẽ đồ thị có tệp dữ liệu ma trận kề Hình 12.5

Lời giải:

Đọc từ trên xuống dưới, từ trái qua phải, ta có các cạnh như sau:

1. Đỉnh 0 kề với đỉnh 2 và 3.

2. Đỉnh 1 kề với đỉnh 2 và 3.

3. Đỉnh 2 kề với đỉnh 0, 1 và 3.

4. Đỉnh 3 kề với đỉnh 0, 1 và 2.

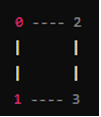
Ta có thể vẽ đồ thị như sau:

Trong đồ thị này, mỗi đỉnh được biểu diễn bởi một số, và mỗi cạnh giữa các đỉnh được biểu diễn bằng các đoạn thẳng nối hai đỉnh tương ứng.

Câu hỏi 2 trang 57 Chuyên đề Tin học 12: Có thể có hai tệp dữ liệu dạng danh sách kề nhau nhưng biểu diễn hai đồ thị hoàn toàn giống nhau không?

Lời giải:

Có, có thể có hai tệp dữ liệu dạng danh sách kề nhau mà biểu diễn hai đồ thị hoàn toàn giống nhau. Điều này có thể xảy ra khi các danh sách kề được sắp xếp khác nhau hoặc khi các đỉnh được đánh số khác nhau, nhưng mối quan hệ kết nối giữa các đỉnh và cạnh vẫn được bảo tồn.

2. Thiết lập đồ thị từ tệp ma trận kề và tệp danh sách tề

Hoạt động 2 trang 58 Chuyên đề Tin học 12: Tìm hiểu, thảo luận cách thiết lập đồ thị (dữ liệu của đồ thị) trong trường hợp tập dữ liệu biểu diễn là ma trận kề hoặc danh sách kề.

Lời giải:

Trong lập trình và xử lý đồ thị, có hai cách phổ biến để biểu diễn dữ liệu của đồ thị: ma trận kề và danh sách kề. Mỗi cách biểu diễn này có những ưu điểm và hạn chế riêng, và việc chọn lựa phụ thuộc vào loại đồ thị và loại thuật toán cụ thể mà bạn muốn thực hiện trên đồ thị đó.

1. Ma trận kề:

Ưu điểm:

Dễ hiểu và dễ thực hiện.

Phù hợp cho việc lưu trữ đồ thị có số lượng cạnh lớn.

Phù hợp cho các thuật toán xử lý đồ thị sử dụng ma trận, như duyệt đồ thị hay tìm đường đi ngắn nhất.

Hạn chế:

Chiếm nhiều không gian lưu trữ, đặc biệt là cho các đồ thị thưa.

Không phù hợp cho việc lưu trữ đồ thị lớn với số lượng đỉnh lớn nhưng số lượng cạnh ít.

2. Danh sách kề:

Ưu điểm:

Tiết kiệm không gian lưu trữ cho các đồ thị thưa, vì chỉ lưu trữ các cạnh thực sự tồn tại.

Phù hợp cho việc lưu trữ đồ thị có số lượng đỉnh lớn nhưng số lượng cạnh ít.

Phù hợp cho việc thêm, xóa cạnh một cách hiệu quả.

Hạn chế:

Khó hiểu hơn so với ma trận kề.

Thời gian truy xuất thông tin của danh sách kề có thể lớn hơn so với ma trận kề, đặc biệt là cho các thuật toán sử dụng ma trận.

Cả hai cách biểu diễn này đều hữu ích và được sử dụng rộng rãi trong thực tế, và lựa chọn giữa chúng phụ thuộc vào yêu cầu cụ thể của bài toán và đặc điểm của dữ liệu đồ thị.

Câu hỏi 1 trang 59 Chuyên đề Tin học 12: Khẳng định dãy Adj[i] có số lượng phần tử bằng số các phần tử có giá trị 1 của hàng thứ i của ma trận kề A là đúng hay sai?

Lời giải:

Khẳng định này là đúng.

Trong ma trận kề A của một đồ thị vô hướng, mỗi hàng iii tương ứng với một đỉnh, và mỗi phần tử trong hàng đó biểu diễn một cạnh nối từ đỉnh iii đến một đỉnh khác. Nếu giá trị của một phần tử là 111, nghĩa là có cạnh nối từ đỉnh iii đến đỉnh tương ứng với vị trí của phần tử đó trong hàng.

Dãy Adj[i] là danh sách kề của đỉnh iii, tức là nó chứa tất cả các đỉnh kề với đỉnh iii. Vậy nếu số lượng phần tử trong Adj[i] bằng số lượng phần tử có giá trị 1 trong hàng thứ i của ma trận kề A, điều đó có nghĩa là mỗi phần tử có giá trị 1 trong hàng thứ i của A tương ứng với một đỉnh kề của đỉnh i, và do đó, khẳng định này là đúng.

Câu hỏi 2 trang 59 Chuyên đề Tin học 12: Khi nào ma trận kề A chỉ gồm toàn số 0?

Lời giải:

Ma trận kề A chỉ gồm toàn số 0 khi không có cạnh nào nối hai đỉnh trong đồ thị. Điều này có thể xảy ra trong trường hợp đồ thị không có cạnh nào, tức là đồ thị không có kết nối giữa các đỉnh. Trong trường hợp này, mỗi phần tử trong ma trận kề đều có giá trị 0, do không có cạnh nối giữa bất kỳ cặp đỉnh nào.

3. Thiết lập đồ thị từ danh sách các cạnh

Hoạt động 3 trang 59 Chuyên đề Tin học 12: Tìm hiểu, thảo luận cách thiết lập dữ liệu của đồ thị trong trường hợp tệp dữ liệu biểu diễn danh sách các cạnh.

Lời giải:

Trong trường hợp tệp dữ liệu biểu diễn danh sách các cạnh của đồ thị, thông tin về cạnh được lưu trữ dưới dạng các cặp hoặc bộ ba đỉnh (tùy thuộc vào loại đồ thị: vô hướng hay có hướng) tương ứng với các cạnh của đồ thị. Cách thiết lập dữ liệu của đồ thị từ tệp dữ liệu này có thể được thực hiện bằng cách đọc từng cặp hoặc bộ ba đỉnh từ tệp dữ liệu và tạo các cạnh tương ứng trong đồ thị.

Dưới đây là một phương pháp tiêu biểu để thiết lập dữ liệu của đồ thị từ tệp dữ liệu biểu diễn danh sách các cạnh:

- Đọc từng dòng từ tệp dữ liệu: Đọc lần lượt từng dòng từ tệp dữ liệu.

- Phân tích mỗi dòng: Phân tích mỗi dòng để lấy thông tin về cạnh. Trong trường hợp đồ thị vô hướng, mỗi dòng thường chứa một cặp đỉnh biểu diễn một cạnh. Trong trường hợp đồ thị có hướng, mỗi dòng thường chứa một bộ ba đỉnh biểu diễn một cạnh, trong đó cả hai đỉnh đầu tiên là đỉnh xuất phát và kết thúc của cạnh, và đỉnh thứ ba có thể là trọng số của cạnh (nếu có).

- Tạo các cạnh: Dựa vào thông tin về cạnh từ mỗi dòng, tạo các cạnh tương ứng trong đồ thị. Trong trường hợp đồ thị vô hướng, mỗi cặp đỉnh tạo thành một cạnh không hướng. Trong trường hợp đồ thị có hướng, mỗi bộ ba đỉnh tạo thành một cạnh có hướng từ đỉnh đầu tiên đến đỉnh thứ hai.

- Lưu trữ thông tin về các cạnh: Lưu trữ thông tin về các cạnh tạo thành từ tệp dữ liệu, chẳng hạn như trong danh sách kề hoặc ma trận kề của đồ thị, để sử dụng cho việc thực hiện các thuật toán và phân tích trên đồ thị sau này.

Phương pháp này cho phép chúng ta tạo đồ thị từ tệp dữ liệu một cách linh hoạt và dễ dàng, và có thể áp dụng cho cả đồ thị vô hướng và có hướng.

Câu hỏi 1 trang 61 Chuyên đề Tin học 12: Một đơn đồ thị, vô hướng có n đỉnh, có thể có số cạnh lớn nhất là bao nhiêu?

Lời giải:

Trong một đơn đồ thị vô hướng có n đỉnh, số cạnh lớn nhất có thể có được là khi mỗi cặp đỉnh đều được nối với nhau bằng một cạnh. Điều này xảy ra khi đồ thị là đồ thị đầy đủ.

Một đồ thị đầy đủ có nnn đỉnh sẽ có tất cả các cặp đỉnh đều được nối với nhau bằng một cạnh.

Số cạnh của một đồ thị đầy đủ với n đỉnh được tính bằng công thức sau:

Do mỗi cặp đỉnh được nối với nhau bằng một cạnh, và số lượng cặp đỉnh là

(lấy một đỉnh, sau đó chọn một đỉnh từ n−1 đỉnh còn lại).

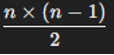
Vì vậy, số cạnh lớn nhất của một đơn đồ thị vô hướng với n đỉnh là

Câu hỏi 2 trang 61 Chuyên đề Tin học 12: Khi nào thì tất cả các phần tử của Adj đều rỗng?

Lời giải:

Ma trận kề Adj của một đồ thị được biểu diễn dưới dạng danh sách kề. Mỗi phần tử của danh sách kề Adj tương ứng với một đỉnh trong đồ thị và chứa các đỉnh kề với đỉnh iii.

Tất cả các phần tử của Adj sẽ rỗng khi không có cạnh nào trong đồ thị, nghĩa là đồ thị không có kết nối giữa các đỉnh. Điều này xảy ra khi ma trận kề tương ứng chỉ chứa các phần tử có giá trị 0.

Do đó, tất cả các phần tử của Adj sẽ rỗng khi ma trận kề chứa toàn bộ các phần tử có giá trị 0, tức là không có cạnh nào nối các đỉnh trong đồ thị.

Luyện tập 1 trang 61 Chuyên đề Tin học 12: Bổ sung thêm đoạn chương trình kiểm tra khi đọc dữ liệu danh sách các cạnh đồ thị của Hoạt động 3 như sau: Với mỗi dòng dữ liệu, nếu hai chỉ số i = j thì bỏ qua dòng này.

Lời giải:

Trong trường hợp tệp dữ liệu biểu diễn danh sách các cạnh của đồ thị, mỗi dòng trong tệp dữ liệu thường chứa một cặp hoặc bộ ba đỉnh biểu diễn một cạnh. Để thiết lập dữ liệu của đồ thị từ tệp dữ liệu này, chúng ta cần đọc từng dòng và tạo các cạnh tương ứng trong đồ thị.

Dưới đây là một phần của chương trình Python để thiết lập dữ liệu của đồ thị từ tệp dữ liệu danh sách các cạnh, và bổ sung kiểm tra khi đọc dữ liệu để loại bỏ các cạnh không hợp lệ (cạnh mà hai đỉnh giống nhau):

def read_edge_list(filename):

edges = []

with open(filename, 'r') as file:

for line in file:

# Split each line to get the vertices of the edge

vertices = line.strip().split()

# Convert vertices to integers

vertices = [int(v) for v in vertices]

# Check if both vertices are the same, then skip this edge

if vertices[0] == vertices[1]:

continue

# Add the edge to the list of edges

edges.append(vertices)

return edges

# Example usage:

edge_list_file = 'edge_list.txt'

edges = read_edge_list(edge_list_file)

print("Edges:", edges)

Trong đoạn mã trên đã đọc từng dòng từ tệp dữ liệu, tách dòng thành các đỉnh của cạnh và sau đó chuyển đổi chúng thành số nguyên. Trước khi thêm cạnh vào danh sách các cạnh, chúng ta kiểm tra xem hai đỉnh có giống nhau không. Nếu hai đỉnh giống nhau, nghĩa là cạnh này không hợp lệ và chúng ta sẽ bỏ qua nó. Cuối cùng, chúng ta trả về danh sách các cạnh đã được xây dựng từ tệp dữ liệu.

Luyện tập 2 trang 61 Chuyên đề Tin học 12: Từ ma trận kề A của đồ thị G có thể tính được số các cạnh của đồ thị không? Nếu được thì tính bằng cách nào?

Lời giải:

Có, từ ma trận kề A của đồ thị G, chúng ta có thể tính được số cạnh của đồ thị bằng cách đếm tổng số lượng phần tử có giá trị 1 trong ma trận kề.

Trong ma trận kề của một đồ thị vô hướng, mỗi cạnh được biểu diễn bởi một phần tử có giá trị 1. Do đó, để tính tổng số cạnh, chúng ta chỉ cần đếm tổng số lượng phần tử có giá trị 1 trong ma trận kề.

Tuy nhiên, trong một đồ thị vô hướng, mỗi cạnh thường được tính hai lần (một lần cho mỗi đỉnh mà nó kết nối). Vì vậy, sau khi đếm số lượng phần tử có giá trị 1 trong ma trận kề, chúng ta cần chia kết quả cho 2 để loại bỏ sự đếm lặp.

Do đó, cách tính số cạnh của đồ thị từ ma trận kề A như sau:

1. Đếm tổng số lượng phần tử có giá trị 1 trong ma trận kề A.

2. Chia kết quả cho 2.

Với một đồ thị vô hướng, số lượng cạnh là nửa số lượng phần tử có giá trị 1 trong ma trận kề.

Vận dụng 1 trang 61 Chuyên đề Tin học 12: Cho ma trận kề A của đồ thị vô hướng G. Viết hàm GraphEdge(A) trả lại danh sách E các cạnh của đồ thị G.

Lời giải:

Để viết hàm GraphEdge(A) trả về danh sách các cạnh của đồ thị vô hướng từ ma trận kề A, chúng ta có thể sử dụng phương pháp duyệt qua ma trận kề và tạo danh sách các cạnh dựa trên các phần tử có giá trị 1.

Dưới đây là cách triển khai hàm này bằng Python:

def GraphEdge(A):

n = len(A)

edges = []

for i in range(n):

for j in range(i+1, n): # Chỉ cần duyệt nửa phần tam giác trên của ma trận

if A[i][j] == 1: # Nếu có cạnh nối từ đỉnh i đến đỉnh j

edges.append((i, j)) # Thêm cạnh vào danh sách cạnh

return edges

# Ví dụ sử dụng

A = [

[0, 1, 1, 0],

[1, 0, 0, 1],

[1, 0, 0, 1],

[0, 1, 1, 0]

]

print(GraphEdge(A)) # In danh sách các cạnh của đồ thị G

Trong hàm này, chúng ta duyệt qua mỗi phần tử của ma trận kề A. Nếu phần tử A[i][j] có giá trị 1 (tức là có cạnh nối từ đỉnh i đến đỉnh j), chúng ta thêm cạnh (i,j) vào danh sách các cạnh. Chúng ta chỉ cần duyệt qua nửa phần tam giác trên của ma trận kề để tránh lặp lại việc đếm các cạnh hai lần. Cuối cùng, chúng ta trả về danh sách các cạnh đã tạo.

Vận dụng 2 trang 61 Chuyên đề Tin học 12: Cho danh sách kề Adj của đồ thị G. Viết hàm GraphEdge(Adj) trả lại danh sách E các cạnh của đồ thị G. Viết chương trình cho hai trường hợp riêng biệt, G là đồ thị vô hướng và G là đồ thị có hướng

Lời giải:

Để viết hàm GraphEdge(Adj) trả về danh sách các cạnh của đồ thị từ danh sách kề Adj, chúng ta cần xác định cách thức biểu diễn cạnh từ danh sách kề. Trong trường hợp đồ thị vô hướng, mỗi cạnh sẽ được biểu diễn một lần. Trong trường hợp đồ thị có hướng, mỗi cạnh sẽ được biểu diễn hai lần (một lần cho mỗi hướng).

Dưới đây là cách triển khai hàm này cho cả hai trường hợp:

• Trường hợp đồ thị vô hướng:

def GraphEdgeUndirected(Adj):

edges = []

for i in range(len(Adj)):

for j in Adj[i]:

if j > i: # Chỉ thêm cạnh một lần, tránh trùng lặp

edges.append((i, j))

return edges

# Sử dụng:

Adj_undirected = [

[1, 2],

[0, 3],

[0, 3],

[1, 2]

]

print(GraphEdgeUndirected(Adj_undirected))

- Trường hợp đồ thị có hướng:

def GraphEdgeDirected(Adj):

edges = []

for i in range(len(Adj)):

for j in Adj[i]:

edges.append((i, j))

return edges

# Sử dụng:

Adj_directed = [

[1, 2],

[3],

[3],

[]

]

print(GraphEdgeDirected(Adj_directed))

Trong cả hai trường hợp, chúng ta duyệt qua mỗi đỉnh trong danh sách kề Adj và tạo các cạnh tương ứng dựa trên thông tin trong danh sách kề. Trong trường hợp đồ thị vô hướng, chúng ta chỉ thêm cạnh một lần (đảm bảo tránh trùng lặp). Trong trường hợp đồ thị có hướng, chúng ta thêm cạnh theo cách thông thường. Cuối cùng, chúng ta trả về danh sách các cạnh đã tạo.