Chuyên đề Tin học 12 Bài 13 (Kết nối tri thức): Thực hành thiết lập đồ thị

Giải Chuyên đề Tin học 12 Bài 13: Thực hành thiết lập đồ thị

Khởi động trang 62 Chuyên đề Tin học 12: Em hãy trao đổi, thảo luận và trả lời một số câu hỏi sau:

– Nếu đồ thị là vô hướng thì ma trận kề có đặc điểm gì?

– Phân biệt sự giống nhau và khác nhau giữa ma trận kề và danh sách kề?

– Khái niệm bậc của các đỉnh có gì khác nhau trong trường hợp đồ thị là vô hướng, có hướng?

Lời giải:

Đặc điểm của ma trận kề đối với đồ thị vô hướng:

- Ma trận kề của đồ thị vô hướng là ma trận vuông.

- Các phần tử trên đường chéo chính của ma trận kề đều bằng 0 (vì không có cạnh nào nối đỉnh với chính nó trong đồ thị vô hướng).

- Ma trận kề là ma trận đối xứng qua đường chéo chính (tức là A[i][j]=A[j][i]) vì mỗi cạnh nối hai đỉnh với nhau được biểu diễn bởi một phần tử có giá trị 1 ở cả hai vị trí tương ứng trong ma trận.

Sự giống nhau và khác nhau giữa ma trận kề và danh sách kề:

- Giống nhau:

+ Cả ma trận kề và danh sách kề đều biểu diễn cấu trúc của đồ thị.

+ Cả hai cách biểu diễn đều cho phép xác định trực tiếp các cạnh của đồ thị.

- Khác nhau:

+ Ma trận kề là một ma trận vuông, trong khi danh sách kề là một danh sách có chiều dài bằng số lượng đỉnh trong đồ thị.

+ Ma trận kề có thể lãng phí không gian lưu trữ nếu đồ thị có ít cạnh, trong khi danh sách kề thường tiết kiệm không gian lưu trữ.

+ Truy cập vào một phần tử của ma trận kề có độ phức tạp thời gian là O(1), trong khi truy cập vào một phần tử của danh sách kề có thể có độ phức tạp thời gian là O(degree) (với degree là bậc của đỉnh tương ứng).

Khái niệm bậc của các đỉnh trong trường hợp đồ thị là vô hướng, có hướng:

+ Trong đồ thị vô hướng, bậc của một đỉnh là số lượng cạnh kề với đỉnh đó. Điều này có thể được tính bằng cách đếm số lượng phần tử có giá trị 1 trong hàng hoặc cột tương ứng của ma trận kề. Trong danh sách kề, bậc của một đỉnh là độ dài của danh sách kề tương ứng với đỉnh đó.

+ Trong đồ thị có hướng, bậc vào (in-degree) của một đỉnh là số lượng cạnh có điểm cuối là đỉnh đó. Bậc ra (out-degree) của một đỉnh là số lượng cạnh có điểm đầu là đỉnh đó.

Luyện tập 1 trang 64 Chuyên đề Tin học 12: Trong Nhiệm vụ 1, hàm In_danh_sach_dinh_ke() lấy thông tin từ ma trận kề A. Có thể sử dụng hàm này với dữ liệu là danh sách kề Adj được không? Nếu có thì viết lại hàm này với dữ liệu đầu vào là danh sách kề Adj.

Lời giải:

Có thể sử dụng hàm In_danh_sach_dinh_ke() để in ra danh sách kề từ dữ liệu là danh sách kề Adj. Dưới đây là phiên bản cải tiến của hàm này để hoạt động với danh sách kề Adj.

def In_danh_sach_dinh_ke(Adj):

for i, neighbors in enumerate(Adj):

print(f"Danh sách kề của đỉnh {i}: {neighbors}")

# Sử dụng:

Adj = [

danh sách kề Adj có trong sách

]

In_danh_sach_dinh_ke(Adj)

Luyện tập 2 trang 64 Chuyên đề Tin học 12: Trong Nhiệm vụ 2, chúng ta có thể thấy các đỉnh kề không được in ra theo thứ tự tăng dần của chỉ số trong biểu diễn danh sách kề. Em hãy giải thích tại sao. Có thể chỉnh sửa chương trình để in ra các đỉnh kề theo thứ tự chỉ số tăng dần được không?

Lời giải:

Trong Nhiệm vụ 2, việc in ra các đỉnh kề không được theo thứ tự tăng dần của chỉ số trong biểu diễn danh sách kề là do cách danh sách kề được xây dựng. Thường thì khi chúng ta thêm một cạnh mới vào danh sách kề của một đỉnh, chúng ta không đảm bảo rằng các đỉnh kề sẽ được thêm vào theo thứ tự tăng dần của chỉ số.

Để in ra các đỉnh kề theo thứ tự chỉ số tăng dần, chúng ta có thể sắp xếp danh sách kề của mỗi đỉnh trước khi in ra. Dưới đây là cách cải tiến chương trình để in ra các đỉnh kề theo thứ tự chỉ số tăng dần:

def In_danh_sach_dinh_ke_sap_xep(Adj):

for i, neighbors in enumerate(Adj):

sorted_neighbors = sorted(neighbors) # Sắp xếp các đỉnh kề theo thứ tự tăng dần

print(f"Danh sách kề của đỉnh {i} (theo thứ tự tăng dần): {sorted_neighbors}")

# Sử dụng:

Adj = [

danh sách kề Adj có trong sách

]

In_danh_sach_dinh_ke_sap_xep(Adj)

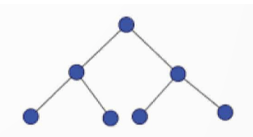
Vận dụng 1 trang 64 Chuyên đề Tin học 12: Cây nhị phân có thể được coi là đồ thị vô hướng, các nút của cây sẽ tương ứng là đỉnh, còn quan hệ cha-con là cạnh nối của đồ thị. Với cây nhị phân hoàn chỉnh, các đỉnh được đánh số theo chỉ số của mảng biểu diễn tương ứng của cây. Hãy tính ma trận kề của đồ thị tương ứng cây nhị phân ở hình bên.

Lời giải:

Để tính ma trận kề của đồ thị tương ứng với cây nhị phân hoàn chỉnh, chúng ta cần xác định cách biểu diễn cây nhị phân hoàn chỉnh bằng mảng và sau đó chuyển đổi thông tin này thành ma trận kề. Trong cây nhị phân hoàn chỉnh, mỗi nút được đánh số theo chỉ số của mảng biểu diễn, và quan hệ cha-con được duy trì bằng cách tính toán chỉ số của các nút cha và con.

Dưới đây là cách tính ma trận kề của đồ thị tương ứng với cây nhị phân hoàn chỉnh:

1. Xác định số lượng đỉnh của cây nhị phân hoàn chỉnh. Số lượng đỉnh của cây nhị phân hoàn chỉnh có thể tính bằng công thức 2n−1, trong đó nnn là số tầng của cây.

2. Khởi tạo ma trận kề A với kích thước n×n và tất cả các phần tử đều bằng 0 ban đầu.

3. Duyệt qua từng nút của cây và thiết lập các cạnh nối trong ma trận kề:

- Nếu nút ở vị trí i có con trái (nếu có) ở vị trí 2i+1 và con phải (nếu có) ở vị trí 2i+2, thì đặt A[i][2i+1]=A[i][2i+2]=1 (do đỉnh i kết nối với đỉnh 2i+1 và 2i+2).

- Lưu ý rằng trong trường hợp số lượng đỉnh của cây không phải là một lũy thừa của 2, một số phần tử cuối cùng của mảng biểu diễn cây sẽ không có nút con, do đó cần kiểm tra điều kiện 2i+1 và 2i+2 có vượt quá số lượng đỉnh của cây hay không trước khi gán cạnh nối.

Một ví dụ chương trình Python thực hiện việc tính ma trận kề của đồ thị tương ứng với cây nhị phân hoàn chỉnh:

def calculate_adjacency_matrix_complete_binary_tree(levels):

n = 2 ** levels - 1 # Số lượng đỉnh của cây nhị phân hoàn chỉnh

A = [[0] * n for _ in range(n)] # Khởi tạo ma trận kề

# Thiết lập cạnh nối giữa các đỉnh

for i in range(n):

left_child = 2 * i + 1

right_child = 2 * i + 2

if left_child < n:

A[i][left_child] = 1

if right_child < n:

A[i][right_child] = 1

return A

# Số tầng của cây nhị phân hoàn chỉnh

levels = 3

# Tính ma trận kề của cây nhị phân hoàn chỉnh với số tầng là levels

adjacency_matrix = calculate_adjacency_matrix_complete_binary_tree(levels)

# In ma trận kề

for row in adjacency_matrix:

print(row)

Trong ví dụ này, chúng ta tính ma trận kề cho một cây nhị phân hoàn chỉnh có 3 tầng và in ra ma trận kề tương ứng. Đảm bảo rằng số tầng nnn là số nguyên không âm.

Vận dụng 2 trang 64 Chuyên đề Tin học 12: Viết lại các hàm thiết lập đồ thị BuildGraph(fname) với tệp dữ liệu đầu vào là danh sách các cạnh của đồ thị. Đầu ra của hàm là dãy các giá trị V, E, A, Adj. Viết hàm cho cả hai trường hợp đồ thị vô hướng và đồ thị có hướng.

Lời giải:

Dưới đây là mã Python cho các hàm thiết lập đồ thị BuildGraph dựa trên danh sách các cạnh của đồ thị:

def BuildGraph(fname):

V = set()

E = []

with open(fname, 'r') as file:

for line in file:

edge = tuple(map(int, line.strip().split())) # Chuyển đổi dòng thành cạnh (u, v)

V.add(edge[0]) # Thêm đỉnh u vào tập đỉnh

V.add(edge[1]) # Thêm đỉnh v vào tập đỉnh

E.append(edge) # Thêm cạnh vào danh sách các cạnh

V = sorted(V) # Sắp xếp tập đỉnh

n = len(V)

# Khởi tạo ma trận kề và danh sách kề

A = [[0] * n for _ in range(n)] # Ma trận kề

Adj = [[] for _ in range(n)] # Danh sách kề

# Điền thông tin vào ma trận kề và danh sách kề

for edge in E:

u, v = edge

A[u][v] = 1 # Đánh dấu cạnh (u, v) trong ma trận kề

Adj[u].append(v) # Thêm v vào danh sách kề của u

return V, E, A, Adj

# Sử dụng hàm BuildGraph cho đồ thị vô hướng

V, E, A, Adj = BuildGraph('graph_edges.txt')

print("Đồ thị vô hướng:")

print("Tập đỉnh:", V)

print("Tập cạnh:", E)

print("Ma trận kề:")

for row in A:

print(row)

print("Danh sách kề:")

for i, neighbors in enumerate(Adj):

print(f"{i}: {neighbors}")

# Sử dụng hàm BuildGraph cho đồ thị có hướng

V, E, A, Adj = BuildGraph('digraph_edges.txt')

print("\nĐồ thị có hướng:")

print("Tập đỉnh:", V)

print("Tập cạnh:", E)

print("Ma trận kề:")

for row in A:

print(row)

print("Danh sách kề:")

for i, neighbors in enumerate(Adj):

print(f"{i}: {neighbors}")

- Trong mã trên:

- Hàm BuildGraph đọc tệp dữ liệu đầu vào và xây dựng các biểu diễn của đồ thị: tập đỉnh VVV, tập cạnh EEE, ma trận kề AAA, và danh sách kề Adj\text{Adj}Adj.

- Hàm đọc dữ liệu từ tệp dựa trên định dạng: mỗi dòng trong tệp biểu diễn một cạnh của đồ thị.

- Các biểu diễn của đồ thị được trả về cho cả hai trường hợp đồ thị vô hướng và có hướng.