Chuyên đề Tin học 12 Bài 14 (Kết nối tri thức): Kĩ thuật duyệt đồ thị theo chiều sâu

Giải Chuyên đề Tin học 12 Bài 14: Kĩ thuật duyệt đồ thị theo chiều sâu

Khởi động trang 65 Chuyên đề Tin học 12: Chúng ta đã biết bài toán và thuật toán duyệt (tìm kiếm) dữ liệu trên các cấu trúc dữ liệu khác nhau:

– Kiểu dữ liệu mảng (một hoặc hai chiều).

– Kiểu dữ liệu cây (cây nhị phân và cây tìm kiếm nhị phân).

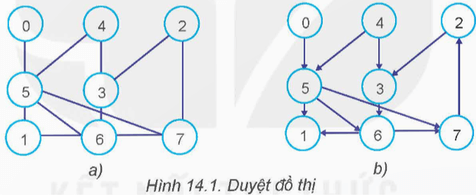
Vậy với dữ liệu của đồ thị, việc duyệt các đỉnh của đồ thị sẽ được thực hiện như thế nào? Quan sát hai đồ thị ở Hình 14.1 và thảo luận với bạn cách thực hiện duyệt trên các đỉnh của đồ thị đó.

Lời giải:

Cách thực hiện duyệt các đỉnh của đồ thị:

- Duyệt theo chiều sâu (DFS): Bắt đầu từ một đỉnh, tiếp tục đi sâu vào đồ thị theo một nhánh cho đến khi không thể đi xa hơn, sau đó quay lại (backtrack) và tiếp tục với nhánh khác.

- Duyệt theo chiều rộng (BFS): Bắt đầu từ một đỉnh, duyệt tất cả các đỉnh kề với nó trước, sau đó mới chuyển sang duyệt các đỉnh ở mức độ sâu tiếp theo.

- Đánh dấu các đỉnh: Khi duyệt, đánh dấu các đỉnh đã thăm để tránh duyệt lại nhiều lần.

- Thứ tự duyệt: Thứ tự duyệt có thể khác nhau tùy thuộc vào cách đồ thị được biểu diễn và thuật toán sử dụng.

1. Bài toán duyệt đồ thị

Hoạt động 1 trang 65 Chuyên đề Tin học 12: Tìm hiểu ý tưởng của thuật toán duyệt đồ thị theo chiều sâu (DFS – Depth First Search).

Lời giải:

Ý tưởng chính của DFS:

DFS hoạt động bằng cách bắt đầu từ một đỉnh nguồn, đánh dấu nó là đã thăm, sau đó tiếp tục đi sâu vào các đỉnh kề chưa thăm cho đến khi không thể đi tiếp được nữa. Khi không thể đi tiếp, thuật toán quay lui về các đỉnh trước đó để tiếp tục tìm kiếm các đường đi mới.

Câu hỏi 1 trang 67 Chuyên đề Tin học 12: Thứ tự các đỉnh trong danh sách kề có ảnh hưởng đến thứ tự các đỉnh được duyệt của thuật toán DFS không?

Lời giải:

Có, thứ tự các đỉnh trong danh sách kề ảnh hưởng đến thứ tự các đỉnh được duyệt của thuật toán DFS. Đây là do cách mà DFS hoạt động: nó sẽ duyệt các đỉnh kề theo thứ tự chúng xuất hiện trong danh sách kề của đỉnh hiện tại.

Cụ thể hơn:

Khi thuật toán DFS thăm một đỉnh v, nó sẽ duyệt qua tất cả các đỉnh kề của v. Nếu danh sách các đỉnh kề của v được sắp xếp theo một thứ tự nhất định, DFS sẽ thăm các đỉnh kề theo đúng thứ tự đó. Điều này có thể dẫn đến các đường đi và thứ tự duyệt khác nhau.

Câu hỏi 2 trang 67 Chuyên đề Tin học 12: Mô tả quá trình duyệt theo chiều sâu của đồ thị có hướng trong Hình 14.1b nếu xuất phát từ đỉnh 4.

Lời giải:

Quá trình duyệt theo chiều sâu (DFS) của đồ thị có hướng bắt đầu từ đỉnh 4 được mô tả như sau:

1. Bắt đầu tại đỉnh 4: Đánh dấu đỉnh 4 là đã thăm.

2. Thăm đỉnh kề: Chọn một trong các đỉnh kề với đỉnh 4 để thăm tiếp theo. Đỉnh 4 có cạnh đi ra đến đỉnh 3 và đỉnh 2.

* Nếu chọn đỉnh 3 trước:

a) Thăm đỉnh 3 và đánh dấu là đã thăm.

b) Tiếp tục thăm đỉnh kề của đỉnh 3 là đỉnh 6.

c) Thăm đỉnh 6 và đánh dấu là đã thăm.

d) Thăm đỉnh kề của đỉnh 6 là đỉnh 7 và đánh dấu là đã thăm.

e) Quay trở lại đỉnh 4 và thăm đỉnh 2, sau đó là đỉnh 7 nếu chưa được thăm.

* Nếu chọn đỉnh 2 trước:

a) Thăm đỉnh 2 và đánh dấu là đã thăm.

b) Thăm đỉnh kề của đỉnh 2 là đỉnh 7 và đánh dấu là đã thăm.

c) Quay trở lại đỉnh 4 và thăm đỉnh 3, sau đó là đỉnh 6 và đỉnh 7 nếu chưa được thăm.

Quá trình này tiếp tục cho đến khi tất cả các đỉnh có thể tiếp cận từ đỉnh xuất phát đã được thăm. Trong DFS, chúng ta sẽ đi sâu vào từng nhánh một cách càng sâu càng tốt trước khi quay trở lại (backtrack).

Hoạt động 2 trang 68 Chuyên đề Tin học 12: Quan sát, thảo luận và tìm hiểu thuật toán duyệt theo chiều sâu trên đồ thị bất kì.

Lời giải:

Khái niệm cơ bản của DFS DFS hoạt động dựa trên ý tưởng:

1. Bắt đầu từ một đỉnh ban đầu.

2. Đánh dấu đỉnh đó là đã thăm.

3. Duyệt qua tất cả các đỉnh kề chưa được thăm của đỉnh hiện tại.

4. Khi không còn đỉnh kề nào chưa thăm, quay lui về đỉnh trước đó để tiếp tục tìm kiếm.

5. Quá trình này tiếp tục cho đến khi tất cả các đỉnh có thể được thăm từ đỉnh ban đầu đều đã được thăm.

Triển khai DFS DFS có thể được triển khai bằng cách sử dụng đệ quy hoặc ngăn xếp.

Câu hỏi 1 trang 69 Chuyên đề Tin học 12: Nếu đồ thị G chỉ bao gồm các đỉnh biệt lập, không có cạnh nào thì thuật toán duyệt sâu DFS sẽ được thực hiện như thế nào?

Lời giải:

Nếu đồ thị G chỉ bao gồm các đỉnh biệt lập, không có cạnh nào nối giữa các đỉnh, thì thuật toán duyệt theo chiều sâu (DFS) sẽ hoạt động một cách đặc biệt vì không có cạnh nào để di chuyển từ một đỉnh này sang đỉnh khác. Hãy xem xét các khía cạnh và quá trình của DFS trong trường hợp này.

* Đặc điểm của đồ thị biệt lập:

1. Các đỉnh biệt lập: Mỗi đỉnh trong đồ thị không có đỉnh kề nào.

2. Không có cạnh: Không có cạnh nào nối giữa các đỉnh.

* Triển khai DFS trên đồ thị biệt lập Khi thực hiện DFS trên đồ thị này, quá trình sẽ như sau:

1. Bắt đầu từ đỉnh đầu tiên: Chọn một đỉnh để bắt đầu (theo thứ tự bất kỳ).

2. Đánh dấu đỉnh đó là đã thăm: Đánh dấu đỉnh hiện tại là đã thăm.

3. Không có đỉnh kề để tiếp tục: Vì không có đỉnh kề nào để di chuyển đến, DFS sẽ không thực hiện bất kỳ bước di chuyển nào.

4. Kết thúc tại đỉnh hiện tại: Quá trình kết thúc cho đỉnh hiện tại vì không có cạnh nào để tiếp tục.

Câu hỏi 2 trang 69 Chuyên đề Tin học 12: Chỉnh sửa hàm DFS() bổ sung lệnh in thông tin của các đỉnh khi duyệt. Ví dụ hàm DFS() có thể viết lại như sau:

Sử dụng hàm trên áp dụng duyệt các phần tử của đồ thị Hình 14.1a trong phần khởi động. Kiểm tra thứ tự các đỉnh đã duyệt có trùng khớp với thứ tự các đỉnh đã duyệt (bằng tay) trong Hoạt động 1 hay không.

Lời giải:

Gợi ý phiên bản chỉnh sửa của hàm DFS() với lệnh in thông tin của các đỉnh khi duyệt:

def DFS(Adj, u, visited=None):

if visited is None:

visited = set()

visited.add(u)

print(f"Duyệt đỉnh {u}") # In thông tin đỉnh u khi duyệt

for v in Adj[u]:

if v not in visited:

DFS(Adj, v, visited)

Hoạt động 3 trang 69 Chuyên đề Tin học 12: Tìm hiểu một cách cài đặt khác của thuật toán duyệt theo chiều sâu DFS không sử dụng kĩ thuật đệ quy.

Lời giải:

Để cài đặt thuật toán duyệt theo chiều sâu (DFS) mà không sử dụng đệ quy, chúng ta có thể sử dụng ngăn xếp (stack) để theo dõi các đỉnh và thực hiện duyệt. Dưới đây là một số cách cài đặt DFS không sử dụng đệ quy:

1. Sử dụng ngăn xếp (Stack):

- Bắt đầu bằng việc đưa một đỉnh bất kỳ vào ngăn xếp.

- Lặp qua các bước sau cho đến khi ngăn xếp trống:

a) Lấy đỉnh trên cùng của ngăn xếp (top value).

b) Đánh dấu đỉnh này là đã thăm (thêm vào danh sách visited).

c) Thêm tất cả các đỉnh kề của đỉnh đang xét vào ngăn xếp, nếu chưa được thăm.

d) Lặp lại bước a) cho đến khi không còn đỉnh kề nào để thêm vào ngăn xếp.

2. Sử dụng hàng đợi (Queue):

- Tương tự như cách sử dụng ngăn xếp, nhưng thay vì ngăn xếp, chúng ta sử dụng hàng đợi.

- Bắt đầu bằng việc đưa một đỉnh bất kỳ vào hàng đợi.

- Lặp qua các bước sau cho đến khi hàng đợi trống:

a) Lấy đỉnh đầu tiên của hàng đợi.

b) Đánh dấu đỉnh này là đã thăm.

c) Thêm tất cả các đỉnh kề của đỉnh đang xét vào hàng đợi, nếu chưa được thăm.

d) Lặp lại bước a) cho đến khi không còn đỉnh kề nào để thêm vào hàng đợi.

3. Sử dụng danh sách liên kết (Linked List):

- Thay vì sử dụng ngăn xếp hoặc hàng đợi, chúng ta có thể sử dụng danh sách liên kết để lưu trữ các đỉnh.

- Bắt đầu bằng việc đưa một đỉnh bất kỳ vào danh sách liên kết.

- Lặp qua các bước sau cho đến khi danh sách liên kết trống:

a) Lấy đỉnh đầu tiên của danh sách liên kết.

b) Đánh dấu đỉnh này là đã thăm.

c) Thêm tất cả các đỉnh kề của đỉnh đang xét vào danh sách liên kết

Câu hỏi 1 trang 71 Chuyên đề Tin học 12: Nếu áp dụng thuật toán duyệt DFS cho đồ thị có hướng Hình 14.1b trong phần khởi động thì thứ tự các đỉnh được đánh dấu sẽ theo thứ tự nào?

Lời giải:

Thứ tự các đỉnh được đánh dấu khi áp dụng thuật toán duyệt theo chiều sâu (DFS) sẽ phụ thuộc vào đỉnh bắt đầu và quy tắc chọn đỉnh kế tiếp khi có nhiều lựa chọn. Nếu giả sử bắt đầu từ đỉnh 0 và chọn đỉnh có số thứ tự nhỏ nhất chưa được thăm, một thứ tự duyệt có thể là:

- Bắt đầu từ đỉnh 0: Đánh dấu đỉnh 0 là đã thăm.

- Tiếp tục đến đỉnh 5: Đánh dấu đỉnh 5 là đã thăm.

- Sau đó đến đỉnh 1: Đánh dấu đỉnh 1 là đã thăm.

- Tiếp tục đến đỉnh 6: Đánh dấu đỉnh 6 là đã thăm.

- Tiếp theo là đỉnh 3: Đánh dấu đỉnh 3 là đã thăm.

- Rồi đến đỉnh 4: Đánh dấu đỉnh 4 là đã thăm.

- Sau đó là đỉnh 2: Đánh dấu đỉnh 2 là đã thăm.

- Cuối cùng là đỉnh 7: Đánh dấu đỉnh 7 là đã thăm.

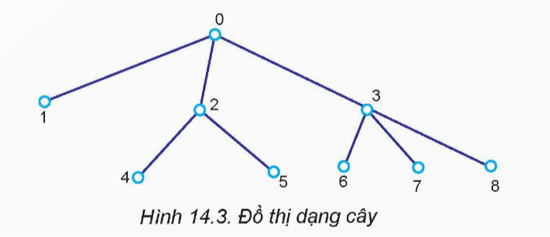
Câu hỏi 2 trang 71 Chuyên đề Tin học 12: Với đồ thị Hình 14.3 thì thứ tự các đỉnh đã duyệt theo chiều sâu, bắt đầu từ đỉnh 0 sẽ như thế nào? (theo cả hai cách đệ quy và không đệ quy).

Lời giải:

Giả sử rằng chúng ta bắt đầu duyệt từ đỉnh 0, thứ tự các đỉnh được duyệt theo chiều sâu (DFS) sẽ như sau:

- Duyệt đệ quy (Recursive):

Thứ tự duyệt có thể là: 0 -> 2 -> 4 -> 5 -> 1 -> 3 -> 6 -> 7 -> 8

- Duyệt không đệ quy (Non-recursive):

Sử dụng ngăn xếp (stack), thứ tự duyệt có thể là: 0 -> 1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7 -> 8

Cả hai phương pháp đều cho kết quả giống nhau vì đây là đồ thị dạng cây và chỉ có một đường đi từ một đỉnh đến đỉnh khác mà không cần quay lui.

Luyện tập 1 trang 71 Chuyên đề Tin học 12: Sửa chương trình của thuật toán DFS không đệ quy sao cho chương trình trong khi duyệt sẽ in ra các bước với thông tin sau:

– Thông tin ngăn xếp (hiện thời).

– Phần tử được lấy ra từ ngăn xếp.

– Phần tử được đánh dấu để chuẩn bị cho bước sau (mark).

Lời giải:

Để sửa đổi chương trình của thuật toán DFS không đệ quy sao cho nó in ra thông tin ngăn xếp hiện thời, phần tử được lấy ra từ ngăn xếp, và phần tử được đánh dấu để chuẩn bị cho bước sau, bạn có thể thực hiện như sau:

def dfs(graph, start):

stack = [start] # Ngăn xếp khởi tạo với đỉnh bắt đầu

visited = set() # Tập hợp các đỉnh đã được thăm

while stack:

# In thông tin ngăn xếp hiện thời

print("Stack hiện thời:", stack)

vertex = stack.pop() # Lấy phần tử từ ngăn xếp

print("Phần tử lấy ra từ ngăn xếp:", vertex)

if vertex not in visited:

print("Phần tử được đánh dấu để chuẩn bị cho bước sau (mark):", vertex)

visited.add(vertex) # Đánh dấu phần tử đã thăm

# Thêm các đỉnh kề vào ngăn xếp

for neighbor in reversed(graph[vertex]):

if neighbor not in visited:

stack.append(neighbor)

return visited

# Đồ thị mẫu dưới dạng danh sách kề

graph = {

'A': ['B', 'C'],

'B': ['A', 'D', 'E'],

'C': ['A', 'F'],

'D': ['B'],

'E': ['B', 'F'],

'F': ['C', 'E']

}

# Thực hiện DFS từ đỉnh 'A'

dfs(graph, 'A')

Giải thích:

- Ngăn xếp (Stack): Ban đầu ngăn xếp chứa đỉnh bắt đầu. Mỗi vòng lặp, bạn in ra ngăn xếp hiện thời.

- Phần tử được lấy ra từ ngăn xếp (vertex): Phần tử trên đỉnh ngăn xếp được lấy ra và in ra.

- Phần tử được đánh dấu (mark): Nếu phần tử chưa được thăm, nó được đánh dấu (thêm vào tập visited) và in ra.

Các bước thực hiện:

- Khởi tạo ngăn xếp với đỉnh bắt đầu (start).

- Trong khi ngăn xếp không rỗng:

In thông tin ngăn xếp hiện thời.

Lấy phần tử từ ngăn xếp và in ra.

Nếu phần tử chưa được thăm:

+ Đánh dấu phần tử đã thăm và in ra.

+ Thêm các đỉnh kề vào ngăn xếp theo thứ tự ngược lại để duyệt đúng thứ tự DFS.

Luyện tập 2 trang 71 Chuyên đề Tin học 12: Hàm DFS(Adj,u) có thể viết theo một cách khác, việc kiểm tra đỉnh u đã đánh dấu chưa được đưa vào bên trong hàm như sau:

a) Trong trường hợp này, phần chương trình chính cần viết lại như thế nào?

b) Viết lại toàn bộ chương trình duyệt đồ thị theo chiều sâu theo hàm mô tả trên. Cách duyệt này có tương đương với cách đã thực hiện trong Hoạt động 2 không?

Lời giải:

a) Phần chương trình chính cần viết lại:

Phần chính của chương trình sẽ khởi tạo danh sách đánh dấu (mark) và gọi hàm DFS từ đỉnh bắt đầu.

def main(graph, start):

# Khởi tạo mảng đánh dấu cho tất cả các đỉnh

mark = {node: False for node in graph}

# Gọi hàm DFS từ đỉnh bắt đầu

DFS(graph, start, mark)

b) Viết lại toàn bộ chương trình duyệt đồ thị theo chiều sâu:

Dưới đây là toàn bộ chương trình với hàm DFS kiểm tra và đánh dấu đỉnh bên trong hàm:

def DFS(graph, u, mark):

if not mark[u]:

mark[u] = True # Đánh dấu đỉnh u

print("Visit:", u) # In ra đỉnh đang được thăm

for v in graph[u]:

DFS(graph, v, mark)

def main(graph, start):

# Khởi tạo mảng đánh dấu cho tất cả các đỉnh

mark = {node: False for node in graph}

# Gọi hàm DFS từ đỉnh bắt đầu

DFS(graph, start, mark)

# Đồ thị mẫu dưới dạng danh sách kề

graph = {

'A': ['B', 'C'],

'B': ['A', 'D', 'E'],

'C': ['A', 'F'],

'D': ['B'],

'E': ['B', 'F'],

'F': ['C', 'E']

}

# Thực hiện DFS từ đỉnh 'A'

main(graph, 'A')

Giải thích:

1. Hàm DFS:

Kiểm tra nếu đỉnh u chưa được đánh dấu.

Đánh dấu đỉnh u và in ra đỉnh đang được thăm.

Duyệt qua các đỉnh kề của u và gọi đệ quy hàm DFS cho từng đỉnh kề đó.

2. Hàm main:

Khởi tạo danh sách đánh dấu (mark) cho tất cả các đỉnh trong đồ thị.

Gọi hàm DFS từ đỉnh bắt đầu (start).

So sánh với cách đã thực hiện trong Hoạt động 2:

Cách duyệt này về cơ bản là tương đương với cách đã thực hiện trong Hoạt động 2 (không đệ quy) về mặt chức năng, tức là cả hai đều thực hiện duyệt đồ thị theo chiều sâu và đảm bảo tất cả các đỉnh đều được thăm một lần. Tuy nhiên, cách đệ quy này dễ hiểu và ngắn gọn hơn, nhưng có thể gặp vấn đề về ngăn xếp đệ quy nếu đồ thị quá lớn (vượt quá giới hạn ngăn xếp của Python). Trong khi đó, cách không đệ quy thường sử dụng ngăn xếp tự quản lý và phù hợp với các đồ thị lớn hơn trong thực tế.

Vận dụng 1 trang 71 Chuyên đề Tin học 12: Viết chương trình in ra thứ tự các đỉnh đã được duyệt bằng thuật toán DFS theo cả hai cách đệ quy và không đệ quy, áp dụng cho đồ thị có hướng Hình 14.1b trong phần Khởi động.

Lời giải:

Chương trình Python mô phỏng thuật toán DFS theo cả hai cách đệ quy và không đệ quy:

* Đệ quy (Recursive):

def DFS_recursive(graph, vertex, visited=None):

if visited is None:

visited = set()

visited.add(vertex)

print(vertex, end=' ')

for neighbor in graph[vertex]:

if neighbor not in visited:

DFS_recursive(graph, neighbor, visited)

# Ví dụ sử dụng:

graph = {

0: [1, 2],

1: [3],

2: [4],

3: [],

4: [5],

5: [3],

6: [5],

7: [6]

}

DFS_recursive(graph, 0)

* Không đệ quy (Non-recursive):

def DFS_non_recursive(graph, start_vertex):

visited = set()

stack = [start_vertex]

while stack:

vertex = stack.pop()

if vertex not in visited:

print(vertex, end=' ')

visited.add(vertex)

# Thêm vào ngăn xếp các đỉnh kề chưa được thăm

stack.extend([neighbor for neighbor in graph[vertex] if neighbor not in visited])

# Ví dụ sử dụng:

graph = {

0: [1, 2],

1: [3],

2: [4],

3: [],

4: [5],

5: [3],

6: [5],

7: [6]

}

DFS_non_recursive(graph, 0)

Vận dụng 2 trang 71 Chuyên đề Tin học 12: Các thuật toán DFS đã mô tả trong các phần trên đều thực hiện trên đồ thị được biểu diễn bằng danh sách kề Adj. Hãy viết lại hàm DFS() được thực hiện trên đồ thị được biểu diễn bằng ma trận kề A.

Lời giải:

Để viết lại hàm DFS thực hiện trên đồ thị được biểu diễn bằng ma trận kề A, chúng ta sẽ cần thay đổi cách truy cập các đỉnh kề từ việc duyệt danh sách kề sang việc duyệt ma trận kề.

Hàm DFS thực hiện trên ma trận kề ( bài mẫu tổng quát):

Giả sử ma trận kề A là một ma trận vuông kích thước n x n với n là số lượng đỉnh, trong đó A[i][j] = 1 nếu có cạnh nối từ đỉnh i đến đỉnh j, ngược lại A[i][j] = 0.

Dưới đây là cách viết lại hàm DFS:

python

Sao chép mã

def DFS(A, u, mark):

n = len(A) # Số lượng đỉnh trong đồ thị

if not mark[u]:

mark[u] = True # Đánh dấu đỉnh u

print("Visit:", u) # In ra đỉnh đang được thăm

for v in range(n):

if A[u][v] == 1 and not mark[v]: # Kiểm tra nếu có cạnh và đỉnh v chưa được thăm

DFS(A, v, mark)

def main(A, start):

n = len(A) # Số lượng đỉnh trong đồ thị

# Khởi tạo mảng đánh dấu cho tất cả các đỉnh

mark = [False] * n

# Gọi hàm DFS từ đỉnh bắt đầu

DFS(A, start, mark)

# Đồ thị mẫu dưới dạng ma trận kề

graph_matrix = [

[0, 1, 1, 0, 0, 0], # A

[1, 0, 0, 1, 1, 0], # B

[1, 0, 0, 0, 0, 1], # C

[0, 1, 0, 0, 0, 0], # D

[0, 1, 0, 0, 0, 1], # E

[0, 0, 1, 0, 1, 0] # F

]

# Thực hiện DFS từ đỉnh 'A' (tương ứng với chỉ số 0)

main(graph_matrix, 0)

Giải thích:

1. Hàm DFS:

Kiểm tra nếu đỉnh u chưa được đánh dấu.

Đánh dấu đỉnh u và in ra đỉnh đang được thăm.

Duyệt qua tất cả các đỉnh v từ 0 đến n-1 (vì n là số đỉnh).

Nếu A[u][v] == 1 (tức là có cạnh từ u đến v) và v chưa được thăm, thì gọi đệ quy DFS cho đỉnh v.

2. Hàm main:

Khởi tạo danh sách đánh dấu (mark) cho tất cả các đỉnh trong đồ thị, ban đầu tất cả đều là False.

Gọi hàm DFS từ đỉnh bắt đầu (start).

Vận dụng 3 trang 71 Chuyên đề Tin học 12: Cho đồ thị G = (V, E) và hai đỉnh s, t bất kì. Chứng minh tính chất: Tồn tại đường đi từ s đến t khi và chỉ khi quá trình duyệt theo chiều sâu từ đỉnh s sẽ duyệt qua đỉnh t, hay nói cách khác, quá trình duệt theo chiều sâu từ đỉnh s sẽ đi qua tất cả các đỉnh nằm trong thành phần liên thông chứa đỉnh s, trong đó có đỉnh t.

Lời giải:

Để chứng minh tính chất: "Tồn tại đường đi từ đỉnh s đến đỉnh t khi và chỉ khi quá trình duyệt theo chiều sâu từ đỉnh s sẽ duyệt qua đỉnh t", chúng ta cần chứng minh hai điều sau:

- Nếu tồn tại đường đi từ đỉnh s đến đỉnh t, thì quá trình duyệt DFS từ đỉnh s sẽ duyệt qua đỉnh t.

- Nếu quá trình duyệt DFS từ đỉnh s duyệt qua đỉnh t, thì tồn tại đường đi từ đỉnh s đến đỉnh t.

Chứng minh điều 1: Nếu tồn tại đường đi từ đỉnh s đến đỉnh t, thì quá trình duyệt DFS từ đỉnh s sẽ duyệt qua đỉnh t

- Giả sử tồn tại đường đi từ đỉnh s đến đỉnh t. Điều này có nghĩa là có một dãy các đỉnh s = v0,v1,v2,…,vk=t sao cho (vi,vi+1) ∈ E với mọi 0 ≤ i< k Khi thực hiện DFS từ đỉnh s, DFS sẽ thăm tất cả các đỉnh mà nó có thể truy cập được từ s. Điều này bao gồm các đỉnh v1,v2,…,vk​ vì chúng liên tiếp nhau trong đường đi từ s đến t.

- Do đó, nếu tồn tại đường đi từ đỉnh s đến đỉnh t, DFS sẽ chắc chắn thăm đỉnh t trong quá trình duyệt.

Chứng minh điều 2: Nếu quá trình duyệt DFS từ đỉnh s duyệt qua đỉnh t, thì tồn tại đường đi từ đỉnh s đến đỉnh t

- Giả sử quá trình duyệt DFS từ đỉnh s duyệt qua đỉnh t. Điều này có nghĩa là DFS đã bắt đầu từ đỉnh s và theo các cạnh của đồ thị, nó đã đến đỉnh t.

- DFS duyệt đồ thị bằng cách đi theo các cạnh của đồ thị, nên mỗi bước từ đỉnh hiện tại đến đỉnh tiếp theo trong quá trình duyệt DFS đều là di chuyển qua các cạnh của đồ thị.

- Nếu DFS đã thăm đỉnh t từ đỉnh s, điều đó có nghĩa là có một dãy các đỉnh bắt đầu từ s và kết thúc tại t sao cho mỗi đỉnh trong dãy này đều có cạnh nối với đỉnh tiếp theo trong dãy.

- Do đó, tồn tại một đường đi từ đỉnh s đến đỉnh t.

Kết luận

Từ hai phần chứng minh trên, ta có thể kết luận rằng:

- Tồn tại đường đi từ đỉnh s đến đỉnh t khi và chỉ khi quá trình duyệt theo chiều sâu từ đỉnh s sẽ duyệt qua đỉnh t.

- Điều này cũng có nghĩa là quá trình duyệt theo chiều sâu từ đỉnh s sẽ đi qua tất cả các đỉnh nằm trong thành phần liên thông chứa đỉnh s, trong đó có đỉnh t.

Nói cách khác, DFS từ đỉnh s sẽ duyệt qua tất cả các đỉnh thuộc cùng một thành phần liên thông với đỉnh s.