Nội dung bài viết

    Xem thêm

    Chứng minh rằng trong mọi tam giác ABC ta đều có

    Với giải Bài 5 trang 99 sgk Toán lớp 10 Hình học được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

    1 4,730 31/08/2024
    Trang trước
    Trang sau  

    Giải Toán 10 Ôn tập cuối năm

    Bài 5 trang 99 Toán lớp 10 Hình học: Chứng minh rằng trong mọi tam giác ABC ta đều có:

    a) a = b cosC + c cosB;

    b) sinA = sinB cosC + sinC cosB;

    c) ha = 2RsinB sinC.

    *Phương pháp giải

    1. Xác định dạng của phương trình và các giá trị đặc biệt liên quan đến sin(x) và cos(x).
    2. Sử dụng các công thức lượng giác cơ bản để đơn giản hóa phương trình.
    3. Giải phương trình sau khi đã đơn giản hóa để tìm các giá trị của x.
    4. Kiểm tra lại các giá trị x tìm được để đảm bảo chúng thỏa mãn phương trình ban đầu.

    *Lời giải:

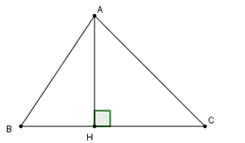
    Tài liệu VietJack

    a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:

    cosC=b2+a2−c22ab; cosB=c2+a2−b22ca

    Ta có: b cosC + c cosB = b.b2+a2−c22ab+c.c2+a2−b22ca

    =b2+a2−c22a+c2+a2−b22a

    =2a22a=a (đpcm).

    b) Theo định lí tổng ba góc của tam giác ta có:

    ˆA+ˆB+ˆC = 180º ⇒ˆA=180°

    ⇒ sinA = sin[180º – (B + C)] = sin(B + C) = sinB.cos C + cosB. sinC (đpcm)

    c) Theo định lí sin trong tam giác ABC, ta có:

    asinA=bsinB=csinC=2R

    ⇒2R.sinB=b

    Do đó: 2R.sinB.sinC=b.sinC=ab.sinCa=2Sa=a.haa=ha (đpcm).

    *Cách giải

    sin2⁡(x)+cos2⁡(x)=1
    sin⁡(2x)=2sin⁡(x)cos⁡(x)
    cos⁡(2x)=cos2⁡(x)−sin2⁡(x)
    sin⁡(x±y)=sin⁡(x)cos⁡(y)±cos⁡(x)sin⁡(y)
    cos⁡(x±y)=cos⁡(x)cos⁡(y)∓sin⁡(x)sin⁡(y)

    Xem thêm lời giải bài tập Toán lớp 10 hay, chi tiết khác:

    Bài 1 trang 98 Toán 10 Hình học: Cho hai vec tơ a→ và b→ có a→=3, b→=5...

    Bài 2 trang 98 Toán 10 Hình học: Cho tam giác ABC và hai điểm M, N sao cho AM→=αAB→, AN→=βAC→...

    Bài 3 trang 99 Toán 10 Hình học: Cho tam giác đều ABC cạnh a.a) Cho M là một điểm trên đường tròn ngoại tiếp..

    Bài 4 trang 99 Toán 10 Hình học: Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC...

    Bài 6 trang 99 Toán 10 Hình học: Cho các điểm A(2; 3), B(9; 4), M(5; y) và P(x; 2). a) Tìm y...

    Bài 7 trang 99 Toán 10 Hình học: Cho tam giác ABC với H là trực tâm. Biết phương trình đường thẳng AB, BH và AH...

    Bài 8 trang 99 Toán 10 Hình học: Lập phương trình đường tròn có tâm nằm trên đường thẳng ∆: 4x + 3y – 2 = 0...

    Bài 9 trang 99 Toán 10 Hình học: Cho elip (E) có phương trình x2100+y236=1. a) Hãy xác định tọa độ các đỉnh...

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 4,730 31/08/2024
    Trang trước
    Trang sau  

    Xem thêm các chương trình khác: