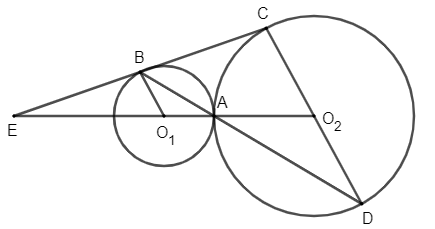
Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A
Lời giải Bài 8 trang 33 Chuyên đề Toán 11 sách Chuyên đề học tập Toán lớp 11 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập.
Giải Chuyên đề Toán 11 Cánh diều Bài 2: Phép đồng dạng
Bài 8 trang 33 Chuyên đề Toán 11: Cho hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A. Tìm phép vị tự biến đường tròn (O1; R) thành đường tròn (O2; 2R).
Lời giải:
Chú ý: Phép vị tự biến đường tròn có bán kính R thành đường tròn có bán kính R' = |k|R và có tâm là ảnh của tâm.
Hai đường tròn (O1; R) và (O2; 2R) tiếp xúc ngoài với nhau tại điểm A và đường tròn tâm O2 có bán kính gấp 2 lần đường tròn tâm O1.
- Trên đường tròn (O1; R) lấy điểm B bất kì.
- Trên đường tròn (O2; 2R) dựng đường kính CD // O1B.
- BC cắt O1O2 tại E.
+) Ta có: O1B // CO2 nên theo định lí Thales có EO2EO1=O2CO1B=2RR=2.
Suy ra →EO2=2→EO1 nên ta có phép vị tự tâm E, tỉ số 2 biến điểm O1 thành điểm O2.
Như vậy, phép vị tự tâm E, tỉ số 2 biến đường tròn (O1; R) thành đường tròn (O2; 2R).
+) Nối B với D, ta chứng minh được BD cắt O1O2 tại điểm tiếp xúc A của hai đường tròn.
Ta có: AO2AO1=2RR=2và A nằm giữa hai điểm O1 và O2 nên →AO2=−2→AO1 . Do đó, ta có phép vị tự tâm A, tỉ số – 2 biến điểm O1 thành điểm O2.
Như vậy, phép vị tự tâm A, tỉ số – 2 biến đường tròn (O1; R) thành đường tròn (O2; 2R).
Vậy có 2 phép vị tự biến đường tròn (O1; R) thành đường tròn (O2; 2R).
Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 26 Chuyên đề Toán lớp 11: Trong mặt phẳng cho điểm O. Với mỗi điểm M trong mặt phẳng...
Luyện tập 1 trang 27 Chuyên đề Toán lớp 11: Cho tam giác ABC có O là trung điểm của cạnh BC..
Hoạt động 3 trang 28 Chuyên đề Toán lớp 11: Cho phép vị tự tâm O tỉ số k và ba điểm A, B, C thẳng hàng...
Hoạt động 4 trang 30 Chuyên đề Toán lớp 11: Trong Hình 53, cho đoạn thẳng AB. Nêu cách dựng:...
Hoạt động 5 trang 31 chuyên đề Toán lớp 11: Quan sát Hình 54 và cho biết:
Bài 3 trang 32 Chuyên đề Toán 11: Khẳng định nào dưới đây là đúng?
Bài 4 trang 32 Chuyên đề Toán 11: Trên bản đồ bay với tỉ lệ xích 1: 10 000 000, khoảng cách giữa Hà Nội,...
Bài 5 trang 33 Chuyên đề Toán 11: Một thấu kính phân kì có tiêu cự OF = OF' = 20 cm (kính cận)...
Bài 12 trang 33 Chuyên đề Toán 11: Hình 59 mô tả một viên gạch trang trí hình tam giác đều...
Xem thêm lời giải bài tập Chuyên đề Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Một vài yếu tố của lí thuyết đồ thị. Đường đi Euler và đường đi Hamilton
Bài 2: Một vài ứng dụng của lí thuyết đồ thị
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều