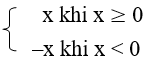Xác định m để hai đường thẳng sau cắt nhau tại một điểm trên trục hoành:$\left(m-1\right)x+my-5=0$ ;$mx+\left(2m–1\right)y+7=0$ . Giá trị m là:

Đáp án đúng: A

*Lời giải:

Hai đường thẳng cắt nhau tại một điểm trên trục hoành suy ra tung độ giao điểm là y=0

Từ đây ta có:

$$\begin{gathered} \left(m-1\right)x-5=0 \\ \iff x=\frac{5}{m-1}\left(m\ne 1\right) \end{gathered}$$ (1)

$$\begin{gathered} mx+7=0 \\ \iff x=-\frac{7}{m}\left(m\ne 0\right) \end{gathered}$$ (2)

Từ (1) và (2) ta có:$\frac{5}{m-1}=-\frac{7}{m}$

$\iff 5m=-7m+7\iff m=\frac{7}{12}\left(n\right)$.

*Phương pháp giải:

 - Sự tương quan giữa hai đường thẳng: Tìm hoành độ giao điểm của hai đường thẳng đó

- Gỉai phương trình hoành độ giao điểm để tìm ra giá trị m

*Lý thuyết cần nắm và dạng bài toán về hàm số: 

 y = ax + b (a ≠ 0)

Tập xác định D = R

Chiều biến thiên

Với a > 0 hàm số đồng biến trên

Với a < 0 hàm số nghịch biến trên

Bảng biến thiên

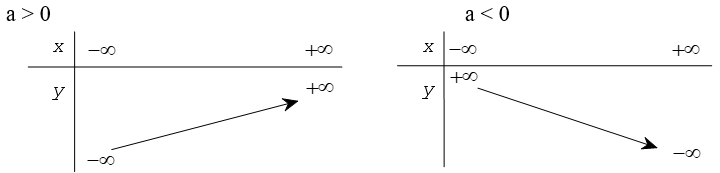
Đồ thị của hàm số là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn song song với đường thẳng y = ax (nếu b ≠ 0) (nếu b ≠ 0) và đi qua hai điểm

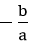
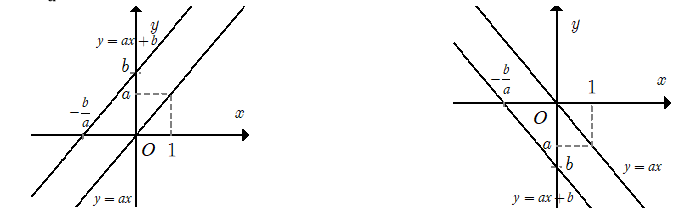
A(0 ; b), B(  ; 0)

 

HÀM SỐ HẰNG y = b

Đồ thị hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm (0 ; b). Đường thẳng này gọi là đường thẳng y = b.

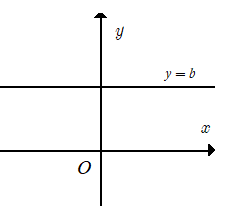
HÀM SỐ y = |x|

Hàm số y = |x| có liên quan chặt chẽ với hàm bậc nhất.

1. Tập xác định

Hàm số y = |x| xác định với mọi giá trị của x ∈ R tức là tập xác định y = |x|.

2. Chiều biến thiên

Theo định nghĩa của giá trị tuyệt đối, ta có y = |x| = 

Từ đó suy ra hàm số y = |x| nghịch biến trên khoảng ( –∞ ; 0) và đồng biến trên khoảng (0 ; +∞).

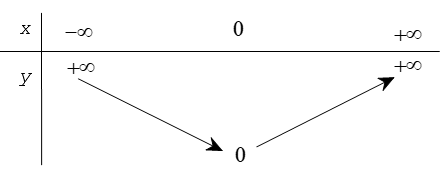
Bảng biến thiên

Khi x > 0 và dần tới +∞ thì y = x dần tới +∞, khi x < 0 dần tới –∞ thì y = –x cũng dần tới +∞. Ta có bảng biến thiên sau

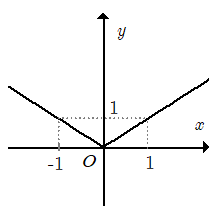
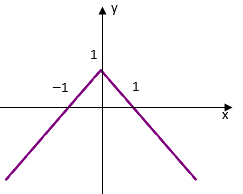
3. Đồ thị

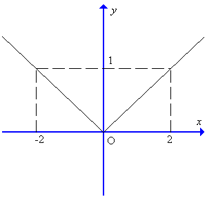
Trong nửa khoảng [0; +∞) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = x.

Trong khoảng (–∞; 0) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = –x

Chú ý:

Hàm số y = |x| là một hàm số chẵn, đồ thị của nó nhận Oy làm trục đối xứng.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Toán 10 Bài 3: Phương trình đường thẳng - Cánh diều

Giải sách bài tập Toán lớp 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng - Cánh diều

Trắc nghiệm Hàm số y = ax + b có đáp án – Toán lớp 10