Câu hỏi:
22/07/2024 9,576Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(3; 4), B(2; 1), C(–1; –2). Cho M(x; y) trên đoạn thẳng BC sao cho SABC = 4SABM. Khi đó x2 – y2 bằng:
A. \(\frac{{13}}{8}\);
B. \(\frac{3}{2}\);
C. \( - \frac{3}{2}\);
D. \(\frac{5}{2}\).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
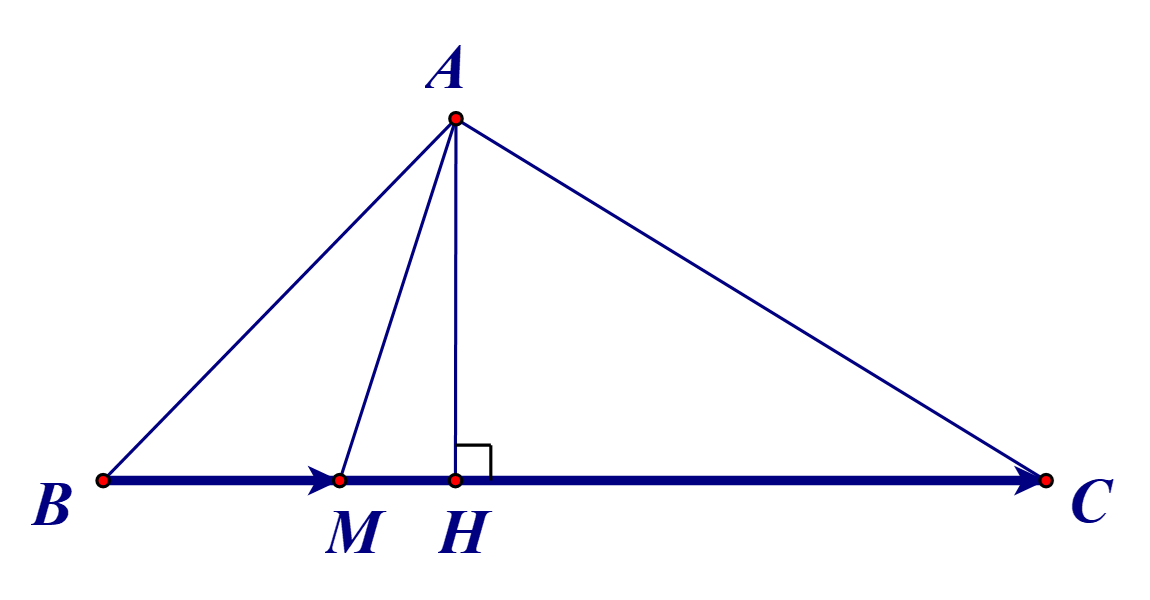
Kẻ AH ⊥ BC tại H.
Ta có:
⦁ \(\overrightarrow {BC} = \left( { - 3; - 3} \right)\). Suy ra \(\frac{1}{4}\overrightarrow {BC} = \left( {\frac{1}{4}.\left( { - 3} \right);\frac{1}{4}.\left( { - 3} \right)} \right) = \left( {\frac{{ - 3}}{4};\frac{{ - 3}}{4}} \right)\);
⦁ \(\overrightarrow {BM} = \left( {x - 2;y - 1} \right)\).
Ta có SABC = 4SABM
Suy ra \(\frac{1}{2}AH.BC = 4.\frac{1}{2}AH.BM\)
Do đó BC = 4BM
Vì vậy \(BM = \frac{1}{4}BC\)
Suy ra \(\overrightarrow {BM} = \frac{1}{4}\overrightarrow {BC} \)
Do đó \(\left\{ \begin{array}{l}x - 2 = - \frac{3}{4}\\y - 1 = - \frac{3}{4}\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}x = \frac{5}{4}\\y = \frac{1}{4}\end{array} \right.\)
Suy ra \({x^2} - {y^2} = {\left( {\frac{5}{4}} \right)^2} + {\left( {\frac{1}{4}} \right)^2} = \frac{{13}}{8}\).
Vậy ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A

Kẻ AH ⊥ BC tại H.
Ta có:
⦁ \(\overrightarrow {BC} = \left( { - 3; - 3} \right)\). Suy ra \(\frac{1}{4}\overrightarrow {BC} = \left( {\frac{1}{4}.\left( { - 3} \right);\frac{1}{4}.\left( { - 3} \right)} \right) = \left( {\frac{{ - 3}}{4};\frac{{ - 3}}{4}} \right)\);
⦁ \(\overrightarrow {BM} = \left( {x - 2;y - 1} \right)\).
Ta có SABC = 4SABM
Suy ra \(\frac{1}{2}AH.BC = 4.\frac{1}{2}AH.BM\)
Do đó BC = 4BM
Vì vậy \(BM = \frac{1}{4}BC\)
Suy ra \(\overrightarrow {BM} = \frac{1}{4}\overrightarrow {BC} \)
Do đó \(\left\{ \begin{array}{l}x - 2 = - \frac{3}{4}\\y - 1 = - \frac{3}{4}\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}x = \frac{5}{4}\\y = \frac{1}{4}\end{array} \right.\)
Suy ra \({x^2} - {y^2} = {\left( {\frac{5}{4}} \right)^2} + {\left( {\frac{1}{4}} \right)^2} = \frac{{13}}{8}\).
Vậy ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho đường tròn (C): x2 + y2 + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:
Câu 2:
Cho elip (E): \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Đường thẳng d: x = –4 cắt (E) tại hai điểm M, N. Khi đó:
Câu 3:
Cho hai điểm A(2; 2), B(5; 1) và đường thẳng ∆: x – 2y + 8 = 0. Lấy điểm C ∈ ∆. Điểm C có hoành độ dương sao cho diện tích tam giác ABC bằng 17. Tọa độ của C là:
Câu 4:
Cho điểm M nằm trên ∆: x + y – 1 = 0 và cách N(–1; 3) một khoảng bằng 5. Khi đó tọa độ điểm M là:


