Câu hỏi:
06/11/2024 177Trong không gian với hệ toạ độ Oxyz, điểm nào dưới đây thuộc trục toạ độ z′Oz.
A. M(-1;0;0).
B. N(1;2;0).
C. P(0;2;0).
D. Q(0;0;-3).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải:
- do thuộc trục tọa độ z'Oz nên điểm sẽ có tọa độ: (0,0,x)
Như vậy đáp án D là đúng
*Phương pháp giải:
- đối chiếu vào hệ trục tọa độ và trên trục tọa độ z'Oz ta sẽ tìm được tọa độ điểm thuộc trục tọa độ z'Oz; tổng quát: (0,0,z)
*Cách giải và các dạng bài toán về hệ trục tọa độ trong không gian:
Hệ trục tọa độ trong không gian
Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz.
• Hệ ba trục như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz, hay đơn giản là hệ tọa độ Oxyz.
• Điểm O được gọi là gốc tọa độ.
• Các mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau được gọi là các mặt phẳng tọa độ.
Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz.
Tọa độ của điểm, tọa độ của vectơ trong không gian
Tọa độ của điểm trong không gian
Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x; y; z) duy nhất sao cho được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết M = (x; y; z) hoặc M(x; y; z), trong đó x là hoành độ, y là tung độ và z là cao độ của M.
Tọa độ của vectơ trong không gian
Trong không gian Oxyz, cho vectơ tùy ý. Bộ ba số (x; y; z) duy nhất sao cho được gọi là tọa độ của vectơ đối với hệ tọa độ Oxyz. Khi đó, ta viết hoặc .
Nhận xét:
- Tọa độ của vectơ cũng là tọa độ của điểm M sao cho
- Trong không gian, cho hai vectơ và . Khi đó, nếu và chỉ nếu .
Tọa độ của vectơ theo tọa độ hai đầu mút
Trong không gian Oxyz, cho hai điểm M(xM; yM; zM) và N(xN; yN; zN). Khi đó: .
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hệ trục toạ độ trong không gian– Toán lớp 12 Kết nối tri thức
TOP 40 câu Trắc nghiệm Hệ tọa độ trong không gian (có đáp án 2024) - Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Gọi M,N lần lượt là các điểm biểu diễn của , trong đó là nghiệm phức của phương trình . Tính diện tích tam giác OMN.
Câu 4:
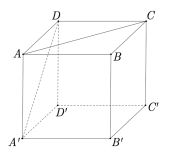
hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng AC và A′D bằng
Câu 5:
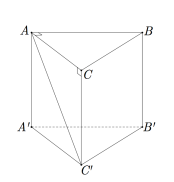
Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác vuông tại A,AB=,AC=AA'=a. Sin góc giữa đường thẳng AC′ và mặt phẳng (BCC′B′) bằng
Câu 6:
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(4;0;1),B(-2;2;3). Phương trình nào dưới đây là phương trình mặt phẳng trung trực của đoạn thẳng AB?
Câu 8:
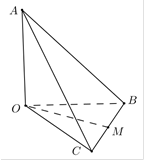
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=OB=a,OC=2a. Gọi M là trung điểm cạnh BC. Côsin góc giữa hai đường thẳng AB và OM bằng
Câu 9:
Cho hàm số (với m là tham số thực) thoả mãn . Mệnh đề nào sau đây đúng ?
Câu 10:
Thể tích khối tròn xoay tạo thành khi quay xung quanh trục Ox hình phẳng giới hạn bởi đường cong y=ln(x+1), trục hoành và hai đường thẳng x=0;x=1 là
Câu 11:
Cho hai số phức thoả mãn và M,N lần lượt là điểm biểu diễn các số phức . Biết . Phần ảo của số phức bằng
Câu 13:
Trong không gian với hệ toạ độ Oxyz, cho mặt cầu (S): và điểm A(1;2;3). Từ A kẻ được ba tiếp tuyến AB,AC,AD đến mặt cầu (S) với A,B,C là các tiếp điểm. Hỏi mặt phẳng (BCD) đi qua điểm nào dưới đây ?
Câu 15:
Cho hàm số f(x) xác định trên thỏa mãn , . Cho =a ln3+b ln2+c, với a,b,c là các số hữu tỷ. Giá trị biểu thức a+b+c bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)