Câu hỏi:
12/07/2024 134
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
Trên mặt phẳng tọa độ Oxy cho tam giác ABC. M, N, P lần lượt là trung điểm cách cạnh BC, CA, AB. Biết M(0; 1); N(-1; 5); P(2; -3). Tọa độ trọng tâm G tam giác ABC là:
A. \(G\left( {\frac{1}{3};1} \right)\);
A. \(G\left( {\frac{1}{3};1} \right)\);
B. G(1; 3);
B. G(1; 3);
C. G(2; -3);
C. G(2; -3);
D. G(1; 1).
D. G(1; 1).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là A
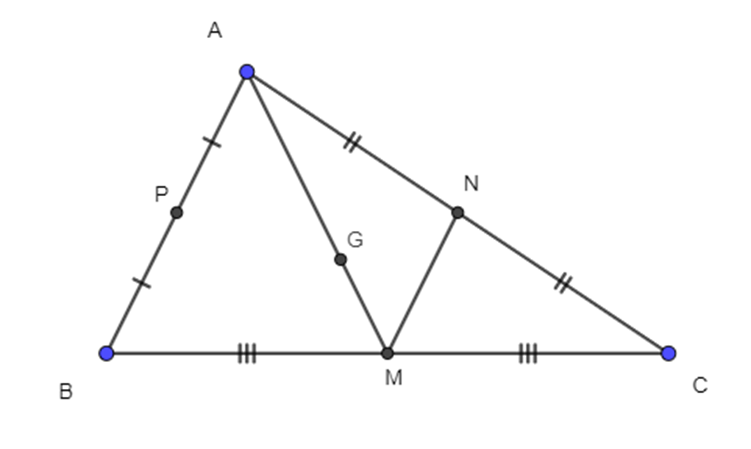
Ta có \(\overrightarrow {MN} \) = (-1; 4)
Gọi tọa độ của điểm A là A(xA; yA). Khi đó \(\overrightarrow {PA} \left( {{x_A} - 2;{y_A} + 3} \right)\).
Ta có \(\overrightarrow {MN} = \overrightarrow {PA} \)(tính chất đường trung bình)
Suy ra \(\left\{ \begin{array}{l}{x_A} - 2 = - 1\\{y_A} + 3 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = 1\end{array} \right.\)
⇒ A(1; 1).
Gọi tọa độ điểm B, C lần lượt là B(xB; yB) và C(xC; yC).
Vì P là trung điểm của AB nên ta có: \(\left\{ \begin{array}{l}{x_B} = 2.2 - 1\\{y_B} = 2.\left( { - 3} \right) - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 3\\{y_B} = - 7\end{array} \right.\)
⇒ B(3; -7).
Vì N là trung điểm của AC nên ta có: \(\left\{ \begin{array}{l}{x_C} = 2.\left( { - 1} \right) - 1\\{y_C} = 2.5 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = - 3\\{y_C} = 9\end{array} \right.\)
⇒ C(-3; 9).
Khi đó tọa độ trọng tâm G là \(\left\{ \begin{array}{l}{x_G} = \frac{{1 + 3 + \left( { - 3} \right)}}{3}\\{y_G} = \frac{{1 + \left( { - 7} \right) + 9}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{1}{3}\\{y_G} = 1\end{array} \right.\)
\( \Rightarrow G\left( {\frac{1}{3};1} \right)\).
Đáp án đúng là A

Ta có \(\overrightarrow {MN} \) = (-1; 4)
Gọi tọa độ của điểm A là A(xA; yA). Khi đó \(\overrightarrow {PA} \left( {{x_A} - 2;{y_A} + 3} \right)\).
Ta có \(\overrightarrow {MN} = \overrightarrow {PA} \)(tính chất đường trung bình)
Suy ra \(\left\{ \begin{array}{l}{x_A} - 2 = - 1\\{y_A} + 3 = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 1\\{y_A} = 1\end{array} \right.\)
⇒ A(1; 1).
Gọi tọa độ điểm B, C lần lượt là B(xB; yB) và C(xC; yC).
Vì P là trung điểm của AB nên ta có: \(\left\{ \begin{array}{l}{x_B} = 2.2 - 1\\{y_B} = 2.\left( { - 3} \right) - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 3\\{y_B} = - 7\end{array} \right.\)
⇒ B(3; -7).
Vì N là trung điểm của AC nên ta có: \(\left\{ \begin{array}{l}{x_C} = 2.\left( { - 1} \right) - 1\\{y_C} = 2.5 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = - 3\\{y_C} = 9\end{array} \right.\)
⇒ C(-3; 9).
Khi đó tọa độ trọng tâm G là \(\left\{ \begin{array}{l}{x_G} = \frac{{1 + 3 + \left( { - 3} \right)}}{3}\\{y_G} = \frac{{1 + \left( { - 7} \right) + 9}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{1}{3}\\{y_G} = 1\end{array} \right.\)
\( \Rightarrow G\left( {\frac{1}{3};1} \right)\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3). Tìm điểm M(x;y) để OABM là một hình bình hành.
Câu 2:
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(-3; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto \(\overrightarrow v = \left( {2;5} \right).\) Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 2 giờ.
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có G là trọng tâm. Cho tọa độ các điểm A(1;3), B(2;4), G(-3;2). Tọa độ điểm C là:
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Trong mặt phẳng tọa độ Oxy, cho hai điểm M(3; -1) và N(2; -5). Điểm nào sau đây thẳng hàng với M, N?
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow u \left( {2;3x - 3} \right)\) và \(\overrightarrow v \left( { - 1; - 2} \right)\). Có bao nhiêu giá trị nguyên của x thỏa mãn \(\left| {\overrightarrow u } \right| = \left| {2\overrightarrow v } \right|\).
Câu 6:
Cho hình vẽ sau:
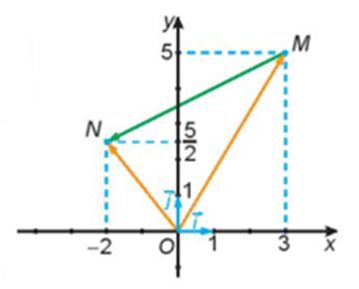
Hãy biểu thị mỗi vecto \(\overrightarrow {OM} ,\overrightarrow {ON} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \).
Cho hình vẽ sau:

Hãy biểu thị mỗi vecto \(\overrightarrow {OM} ,\overrightarrow {ON} \) theo các vecto \(\overrightarrow i ,\overrightarrow j \).
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2). Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD. Tổng x + y bằng
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2). Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD. Tổng x + y bằng
Câu 8:
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 5\overrightarrow i + 6\overrightarrow j .\) Khi đó tọa độ của vectơ \(\overrightarrow u \)là:
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = - 5\overrightarrow i + 6\overrightarrow j .\) Khi đó tọa độ của vectơ \(\overrightarrow u \)là:
Câu 9:
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow b \left( {4; - 1} \right)\) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để \(\overrightarrow {MN} = \overrightarrow b \).
Trong mặt phẳng tọa độ Oxy, cho các vecto \(\overrightarrow b \left( {4; - 1} \right)\) và các điểm M(-3x; -1), N(0; -2 + y). Tìm điều kiện của x và y để \(\overrightarrow {MN} = \overrightarrow b \).
Câu 10:
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
\(\overrightarrow x \)(-1; 3); \(\overrightarrow y \left( {2; - \frac{1}{3}} \right)\) ; \(\overrightarrow z \left( { - \frac{2}{5};\frac{1}{5}} \right)\); \(\overrightarrow {\rm{w}} \)(4; -2).
Trong các vectơ sau đây, có bao nhiêu cặp vectơ cùng phương?
\(\overrightarrow x \)(-1; 3); \(\overrightarrow y \left( {2; - \frac{1}{3}} \right)\) ; \(\overrightarrow z \left( { - \frac{2}{5};\frac{1}{5}} \right)\); \(\overrightarrow {\rm{w}} \)(4; -2).
Câu 11:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2). Nhận xét nào sau đây đúng nhất về tam giác OMN.
Câu 12:
Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
Trong mặt phẳng tọa độ Oxy cho các điểm A(11; –2), B(4; 10); C(-2; 2); D(7; 6); Hỏi G(3; 6) là trọng tâm của tam giác nào trong các tam giác sau đây?
Câu 13:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
Trong mặt phẳng tọa độ Oxy, cho B(1; 2) và C(3; -1). Độ dài \(\overrightarrow {BC} \) là:
Câu 14:
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.
Trong mặt phẳng tọa độ Oxy, cho các điểm \(A\left( {k - \frac{1}{3};5} \right)\), B(-2; 12) và
C\(\left( {\frac{2}{3};k - 2} \right)\). Giá trị dương của k thuộc khoảng nào dưới đây thì ba điểm A, B, C thẳng hàng.


