Câu hỏi:
08/10/2024 1,150Tổng bình phương các nghiệm của phương trình 3log3(x−1)−log13(x−5)3=3 bằng
A. 36
B. 32
C. 16−6√7
D. 16+6√7
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Phương pháp giải:
- Tìm điều kiện xác định cho hàm bên trong log để hàm đó xác định trước
- Áp dụng các tính chất về hàm log để tính toán phép tính, cách đổi cơ số của hàm log,..
*Lời giải:
ĐK: .
Ta có: 3log3(x−1)−log13(x−5)3=3⇔3log3(x−1)+3log3(x−5)=3
⇔log3(x−1)+log3(x−5)=1⇔log3[(x−1)(x−5)]=1⇔(x−1)(x−5)=3
⇔x2−6x+2=0⇔x=3±√7
Đối chiếu điều kiện suy ra phương trình có 1 nghiệm x=3+√7⇒x2=16+6√7 .
* Các dạng bài toán về phương trình logarit:
+ Dạng 1. Phương trình loogarit cơ bản
* Phương pháp giải: Xét phương trình lôgarit cơ bản:logaf(x)=b,a, b>0, a≠1
Bước 1: Nêu điều kiện để f(x) có nghĩa
Bước 2: Giải phương trình logaf(x)=b⇔f(x)=ab
Bước 3: Kết luận nghiệm của phương trình.
+ Dạng 2. Phương pháp đưa về cùng cơ số
* Phương pháp giải: Xét phương trình cùng cơ số: logaf(x)=logag(x),0<a≠1
Bước 1: Nêu điều kiện {f(x)>0g(x)>0
Bước 2 Giải phương trình:
logaf(x)=logag(x)⇔f(x)=g(x)
Bước 3: So sánh với điều kiện và kết luận.
+ Dạng 3. Phương pháp đặt ẩn phụ
* Phương pháp giải: Xét phương trình:f[logag(x)]=0(0<a≠1)
Bước 1: Đặt điều kiện: g(x) > 0
Bước 2: Đặt t=logag(x)
Giải phương trình f(t) = 0, tìm t.
Bước 3: Thay vào phương trình: t=logag(x), tìm x.
Bước 4: Kết hợp với điều kiện và kết luận.
+ Dạng 4. Phương pháp mũ hóa
* Phương pháp giải: Xét phương trình: logag(x)=f(x)(0<a≠1)
Bước 1: Đặt điều kiện g(x) > 0
Bước 2: Giải phương trình:
logag(x)=f(x)(0<a≠1)⇔g(x)=af(x)
Bước 3: Kết hợp với điều kiện, kết luận nghiệm.
Xem thêm các bài viết liên quan hay, chi tiết:
Trắc nghiệm Logarit (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y=m2x4−(m2−2020m)x2+3 có đúng một điểm cực trị?
Câu 2:
Trên mặt phẳng (P) cho ba hình tròn bán kính a tâm là O1;O2;O3 đôi một tiếp xúc ngoài với nhau. Ba hình tròn đó là ba đáy của ba hình nón mà các đỉnh tương ứng là ba điểm S1,S2,S3 nằm cùng phía đối với mặt phẳng (P) và cùng cách (P) một khoảng 2a√2 . Mặt cầu tiếp xúc với (S1S2S3) và tiếp xúc ngoài với ba hình nón trên có bán kính bằng
Câu 3:
Có tất cả bao nhiêu số nguyên m∈(−2020;2020) để phương trình log23x2+3x+m+12x2−x+1=x2−5x+2−m
có hai nghiệm phân biệt x1,x2 thỏa mãn x31+x32≥155 ?
Câu 4:
Cho hình hộp ABCD.A'B'C'D' có AB' vuông góc với mặt phẳng đáy (ABCD); góc giữa đường thẳng AA' với (ABCD) bằng 45°. Khoảng cách từ A đến các đường thẳng BB' và DD' bằng 1. Góc giữa hai mặt phẳng (BB' và mặt phẳng bằng 60°. Thể tích khối hộp đã cho bằng
Câu 5:
Cho hàm số f(x) có bảng biến thiên như sau
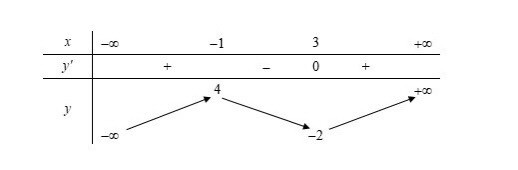
Số nghiệm thực của phương trình 2f(x)-8=0 là
Câu 7:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và B'D' bằng
Câu 8:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai tiệm cận đứng
Câu 9:
Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau
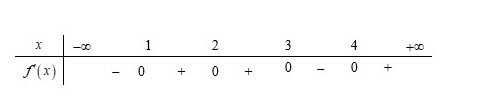
Các khoảng nghịch biến của hàm số là
Câu 11:
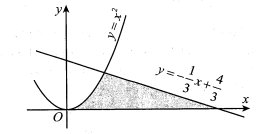
Ông An có một khu vườn giới hạn bởi một đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ Oxy như hình vẽ bên thì parabol có phương trình và đường thẳng . Ông An dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi một đường thẳng đi qua O và điểm M trên parabol để trồng một loại hoa. Tính độ dài OM để diện tích mảnh vườn bằng .
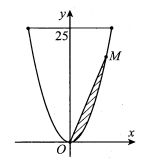
Câu 13:
Trong không gian Oxyz, cho tam giác ABC có . Đường trung tuyến AM của tam giác ABC có phương trình là
Câu 14:
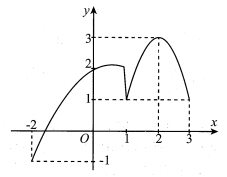
Cho hàm số f(x) liên tục trên đoạn và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên . Giá trị của bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)