Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: →0=0.→i+0.→j⇒→0(0;0).
Vậy tọa độ của →0 là →0(0;0).
Ta có: →0=0.→i+0.→j⇒→0(0;0).
Vậy tọa độ của →0 là →0(0;0).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho →u=(2;−3),→v=(4;1),→a=(8;−12).
a) Hãy biểu thị mỗi vecto →u,→v,→a theo các vecto →i,→j.
b) Tìm tọa độ của các vecto →u+→v,4→u.
c) Tìm mối liên hệ giữa hai vecto →u,→a.
Trong mặt phẳng tọa độ Oxy, cho →u=(2;−3),→v=(4;1),→a=(8;−12).
a) Hãy biểu thị mỗi vecto →u,→v,→a theo các vecto →i,→j.
b) Tìm tọa độ của các vecto →u+→v,4→u.
c) Tìm mối liên hệ giữa hai vecto →u,→a.
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho các vecto →a=3→i−2→j,→b(4;−1) và các điểm M(-3;6), N(3;-3).
a) Tìm mối liên hệ giữa các vecto →MN và 2→a−→b.
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x;y) để OMPN là hình bình hành.
Trong mặt phẳng tọa độ Oxy, cho các vecto →a=3→i−2→j,→b(4;−1) và các điểm M(-3;6), N(3;-3).
a) Tìm mối liên hệ giữa các vecto →MN và 2→a−→b.
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x;y) để OMPN là hình bình hành.
Câu 3:
Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ dự báo.
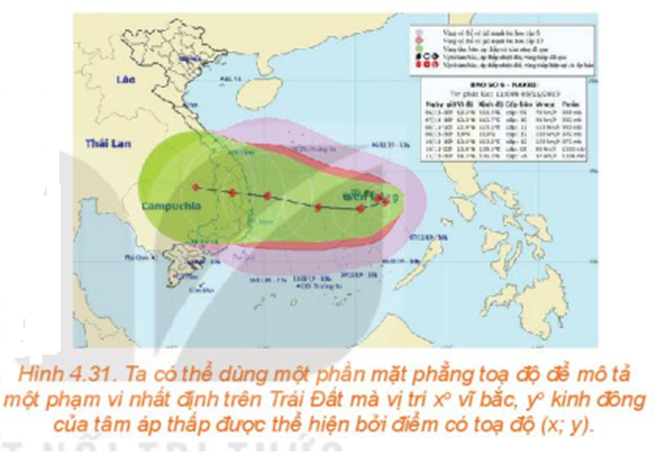
Trong 12 giờ, tâm bão được dự báo di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3). Gọi tọa độ của M là (x;y). Bạn hãy tìm mối liên hệ giữa hai vecto →AM và →AB rồi thể hiện mối quan hệ đó theo tọa độ để tìm x; y.
Từ thông tin dự báo bão được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ dự báo.

Trong 12 giờ, tâm bão được dự báo di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3). Gọi tọa độ của M là (x;y). Bạn hãy tìm mối liên hệ giữa hai vecto →AM và →AB rồi thể hiện mối quan hệ đó theo tọa độ để tìm x; y.
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x;y) để OABM là một hình bình hành.
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2;1), B(3;3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x;y) để OABM là một hình bình hành.
Câu 5:
Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. ,Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?
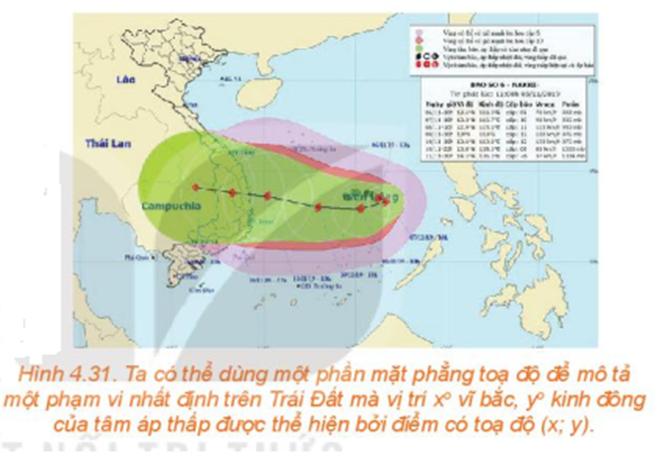
Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ. ,Trong thời gian đó, tâm bão di chuyển thẳng đều từ vị trí có tọa độ (13,8; 108,3) đến vị trí tọa độ (14,1; 106,3). Dựa vào thông tin trên, liệu ta có thể dự đoán được vị trí của tâm bão tại thời điểm bất kì trong khoảng thời gian 12 giờ đó hay không?

Câu 6:
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(1;2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto →v=(3;4). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Sự chuyển động của một tàu thủy được thể hiện trên một mặt phẳng tọa độ như sau: Tàu khởi hành từ vị trí A(1;2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vecto →v=(3;4). Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Câu 7:
Trong Hình 4.33:
a) Hãy biểu thị mỗi vecto →OM,→ON theo các vecto →i,→j.
b) Hãy biểu thị vecto →MN theo các vecto →OM,→ON từ đó biểu thị vecto →MN theo các vecto →i,→j.
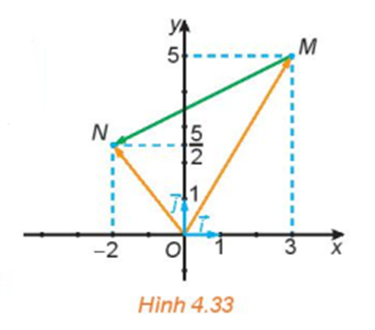
Trong Hình 4.33:
a) Hãy biểu thị mỗi vecto →OM,→ON theo các vecto →i,→j.
b) Hãy biểu thị vecto →MN theo các vecto →OM,→ON từ đó biểu thị vecto →MN theo các vecto →i,→j.

Câu 8:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2).
a) Tính độ dài của các đoạn thẳng OM, ON, MN.
b) Chứng minh rằng tam giác OMN vuông cân.
Trong mặt phẳng tọa độ Oxy, cho các điểm M(1;3), N(4;2).
a) Tính độ dài của các đoạn thẳng OM, ON, MN.
b) Chứng minh rằng tam giác OMN vuông cân.
Câu 9:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x’; y’).
a) Tìm tọa độ của các vecto →OM,→ON.
b) Biểu thị vecto →MN theo các vecto →OM,→ON và tìm tọa độ của →MN.
c) Tìm độ dài của vecto →MN.
Trong mặt phẳng tọa độ Oxy, cho các điểm M(x; y) và N(x’; y’).
a) Tìm tọa độ của các vecto →OM,→ON.
b) Biểu thị vecto →MN theo các vecto →OM,→ON và tìm tọa độ của →MN.
c) Tìm độ dài của vecto →MN.
Câu 10:
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2).
a) Hãy giải thích vì sao các điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trung điểm M của đoạn thẳng AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD.
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;3), B(2;4), C(-3;2).
a) Hãy giải thích vì sao các điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trung điểm M của đoạn thẳng AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm điểm D(x; y) để O(0;0) là trọng tâm tam giác ABD.
Câu 11:
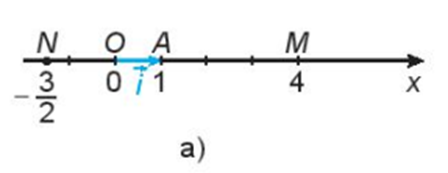
Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt →OA=→i (H.4.32a). Gọi M là điểm biểu diễn số 4, N là điểm biểu diễn số −32. Hãy biểu thị mỗi vecto →OM,→ON theo vecto đơn vị →i.

Câu 12:
Trong Hình 4.38, quân mã đang vị trí có tọa độ (1;2). Hỏi sau một nước đi, quân mã có thể đến những vị trí nào?


Câu 13:
Trong mặt phẳng toạ độ Oxy, cho điểm M(x0;y0) . Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).
a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị →OP theo →i và tính độ dài của →OP theo x0.
b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị →OQ theo →j và tính độ dài của →OP theo y0.
c) Dựa vào hình chữ nhật OPMQ, tính độ dài của →OM theo x0, y0.
d) Biểu thị →OM theo các vecto →i,→j.
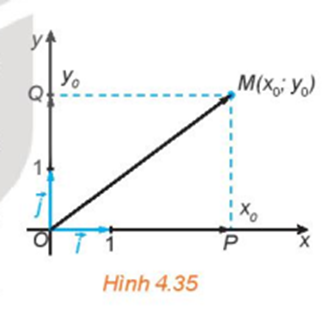
Trong mặt phẳng toạ độ Oxy, cho điểm M(x0;y0) . Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35).
a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị →OP theo →i và tính độ dài của →OP theo x0.
b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị →OQ theo →j và tính độ dài của →OP theo y0.
c) Dựa vào hình chữ nhật OPMQ, tính độ dài của →OM theo x0, y0.
d) Biểu thị →OM theo các vecto →i,→j.


