Tìm giá trị cực đại của hàm số $y=x^3-3x+2$.

Đáp án đúng là A

Lời giải

$y=x^3-3x+2$

$y\text{'}=3x^2-3$

$y\text{'}=0\Rightarrow 3x^2-3=0\iff \left\{\begin{array}{l}x=1\Rightarrow y=0\\ x=-1\Rightarrow y=4\end{array}\right.$

BBT

Vậy giá trị cực đại bằng 4

*Phương pháp giải:

1.Tính đạo hàm y'

2.Tìm nghiệm của đạo hàm

3.Lập bảng biến thiên

4.Tìm x cực đại thay vào y tìm y cực đại

*Lý thuyết:

- Định nghĩa.

Cho hàm số y = f(x) xác định và liên tục trên khoảng (a; b) (có thể a là $-\infty$; b là $+\infty$) và điểm x₀$\in$(a; b).

a) Nếu tồn tại số h > 0 sao cho f(x) < f(x₀) với mọi x(x₀ – h; x₀ + h) và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực đại tại x₀.

b) Nếu tồn tại số h > 0 sao cho f(x) > f(x₀) với mọi x$\in$(x₀ – h; x₀ + h) và $x\ne x_0$ thì ta nói hàm số f(x) đạt cực tiểu tại x₀.

- Chú ý:

1. Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x₀ thì x₀ được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x₀) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số.

Kí hiệu là f_CĐ (f_CT) còn điểm M(x₀; f(x₀)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

2. Các điểm cực đại, cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.

3. Dễ dàng chứng minh được rằng, nếu hàm số y = f(x) có đạo hàm trên khoảng (a; b) và đạt cực đại hoặc cực tiểu tại x₀ thì f’(x₀) = 0.

II. Điều kiện đủ để hàm số có cực trị

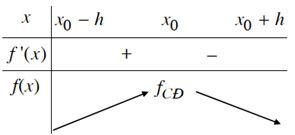
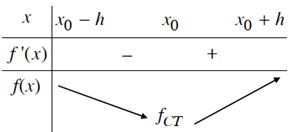
- Định lí 1

Giả sử hàm số y = f(x) liên tục trên khoảng K = (x₀ – h; x₀ + h) và có đạo hàm trên K hoặc trên K \ {x₀}; với h > 0.

a) Nếu f’(x) > 0 trên khoảng (x₀ – h; x₀) và f’(x) < 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực đại của hàm số f(x).

b) Nếu f’(x) < 0 trên khoảng (x₀ – h; x₀) và f’(x) > 0 trên khoảng (x₀; x₀ + h) thì x₀ là một điểm cực tiểu của hàm số f(x).

Xem thêm

Lý thuyết Cực trị của hàm số (mới 2024 + Bài Tập) – Toán 12 

TOP 40 câu Trắc nghiệm Cực trị hàm số (có đáp án 2024) - Toán 12