Tập nghiệm của phương trình $\sqrt[4]{x-\sqrt{x^2-1}}+\sqrt{x+\sqrt{x^2-1}}=2$ là:

Tổng các bình phương các nghiệm của phương trình $\left(x-1\right)\left(x-3\right)+3\sqrt{x^2-4x+5}-2=0$ là:

Số nghiệm của phương trình $x^2-2x-8=4\sqrt{\left(4-x\right)\left(x+2\right)}$ là:

Cho hàm số f(x) xác định trên R có đồ thị như hình vẽ.

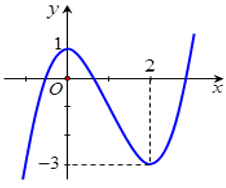
Phương trình $2f\left(x\right)-1=0$ có bao nhiêu nghiệm?

Tổng bình phương các nghiệm của phương trình $x^2+5x+2+2\sqrt{x^2+5x+10}=0$ là:

Cho phương trình $x^3-\left(2m+1\right)x^2+\left(4m-1\right)x-2m+1=0$. Tìm m để phương trình có một nghiệm duy nhất?

Tìm phương trình đường thẳng $d:y=ax+b$. Biết đường thẳng d đi qua điểm I(1; 3) và tạo với hai tia Ox, Oy một tam giác có diện tích bằng 6?

Giả sử phương trình $2x^2-4mx-1=0$ (với m là tham số) có hai nghiệm $x_1, x_2$. Tìm giá trị nhỏ nhất của biểu thức $T=\left|x_1-x_2\right|$

Gọi S là tập hợp các giá trị của tham số m sao cho parabol (P): $y=x^2-4x+m$ cắt Ox tại hai điểm phân biệt A, B thỏa mãn OA = 3OB. Tính tổng T các phần tử của S.

Tìm m để phương trình $\left(m-1\right)x^4-m{x}^2+m^2-1=0$ có ba nghiệm phân biệt.

Có tất cả bao nhiêu giá trị nguyên không dương của tham số m để phương trình $\sqrt{2x+m}=x-1$ có nghiệm duy nhất?

Tập hợp tất cả các giá trị của tham số m để phương trình $\sqrt{1+x}+\sqrt{1-x}+4\sqrt{1-x^2}=m$ có nghiệm là:

Tìm tất cả các giá trị của m để phương trình $x^2-2x-3-m=0$ có nghiệm $x\in \left[0;4\right]$

Phương trình $x^4-5x^3+8x^2-10x+4=0$ có bao nhiêu nghiệm nguyên?

Cho hàm số $y=x^2-2x-2$ có đồ thị (P), và đường thẳng (d) có phương trình $y=x+m$. Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho $O{A}^2+O{B}^2$ đạt giá trị nhỏ nhất

Phương trình $\sqrt[3]{x+5}+\sqrt[3]{x+6}=\sqrt[3]{2x+11}$ có bao nhiêu nghiệm?