Câu hỏi:
17/07/2024 143
Tam giác ABC có AB = \(2\sqrt 2 \), AC = \(2\sqrt 3 \) và độ dài đường cao AH = 2. Khi đó diện tích tam giác ABC bằng:
A. 3 + 3\(\sqrt 3 \);
B. 2 + 3\(\sqrt 2 \);
C. 3 + 2\(\sqrt 2 \);
D. 2 + 2\(\sqrt 2 \).
Đáp án chính xác
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
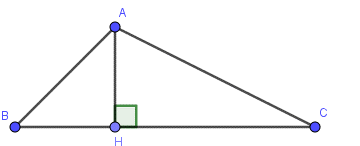
Áp dụng định lý Pythagore ta có:
BH = \(\sqrt {A{B^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {2^2}} = 2\)
Tương tự: CH = \(\sqrt {A{C^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} - {2^2}} = 2\sqrt 2 \).
Do đó BC = BH + CH = 2 + 2\(\sqrt 2 \).
Vậy diện tích tam giác ABC là: S = \(\frac{1}{2}\)AH.BC = \(\frac{1}{2}\). 2. (2 + 2\(\sqrt 2 \)) = 2 + 2\(\sqrt 2 \).
Hướng dẫn giải:
Đáp án đúng là: D.
Áp dụng định lý Pythagore ta có:
BH = \(\sqrt {A{B^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} - {2^2}} = 2\)
Tương tự: CH = \(\sqrt {A{C^2} - A{H^2}} = \sqrt {{{\left( {2\sqrt 3 } \right)}^2} - {2^2}} = 2\sqrt 2 \).
Do đó BC = BH + CH = 2 + 2\(\sqrt 2 \).
Vậy diện tích tam giác ABC là: S = \(\frac{1}{2}\)AH.BC = \(\frac{1}{2}\). 2. (2 + 2\(\sqrt 2 \)) = 2 + 2\(\sqrt 2 \).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC có a = 5, b = 7, cos C = 0,6. Tính diện tích tam giác ABC.
Xem đáp án »
20/07/2024
800
Câu 2:
Tam giác ABC có a = 10, b = 21, c = 17. Diện tích tam giác ABC bằng:
Xem đáp án »
22/07/2024
249
Câu 4:
Tam giác ABC có BC = a và CA = b. Tam giác ABC có diện tích lớn nhất khi góc C bằng:
Xem đáp án »
18/07/2024
177
Câu 5:
Hình bình hành ABCD có AB = a, BC = 2a và \(\widehat {ABC} = 60^\circ \). Khi đó hình bình hành có diện tích bằng:
Xem đáp án »
13/07/2024
160
Câu 6:
Cho tam giác ABC có AB = 5 , \(\widehat A = 30^\circ \), \(\widehat B = 75^\circ \). Tính diện tích tam giác ABC.
Xem đáp án »
18/07/2024
147
Câu 7:
Tam giác đều nội tiếp đường tròn bán kính R = 8 cm có diện tích là:
Xem đáp án »
13/07/2024
143
Câu 8:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu cạnh AB tăng lên 3 lần, cạnh AC tăng lên 4 lần và giữ nguyên độ lớn của góc A thì khi đó diện tích của tam giác mới được tạo nên bằng:
Xem đáp án »
16/07/2024
115
Câu 9:
Diện tích của một lá cờ hình tam giác cân (như hình dưới) có độ dài cạnh bên là 80 cm và góc ở đỉnh là 50° gần với giá trị nào nhất?
Xem đáp án »
15/07/2024
113
Câu 10:
Cho tam giác ABC có \(a = 4\sqrt 3 \); b = 4 và \(\widehat C = 60^\circ \). Tính diện tích tam giác ABC.
Xem đáp án »
13/07/2024
107
Câu 11:
Cho tam giác ABC có b = 10, c = 15 và \(\widehat A = 30^\circ \). Diện tích tam giác ABC là:
Xem đáp án »
13/07/2024
101
