Câu hỏi:
17/11/2024 236
Nếu hàm số y = f(x) đồng biến trên khoảng (-1,2) thì hàm số y = f(x + 2) đồng biến trên khoảng nào trong các khoảng sau đây?
A. (-1;2)
B. (-3;0)
C. (-2;4)
D. (1;4)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B
*Lời giải
Hàm số y = f(x) đồng biến trên khoảng (−1; 2)⇒f'.
Xét hàm số .
Ta có .
Vậy hàm số y = f(x + 2) đồng biến trên khoảng (-3;0)
*Phương pháp giải
- Do y = f(x) đồng biến trên khoảng (-1,2) nên f'(x) > 0 và x thuộc (-1.2)
- Như vậy hàm số: f(x+2): Tính đạo hàm và xét cho đạo hàm > 0
* Lý thuyết cần nắm và một số dạng toán về sự đồng biến, nghịch biến của hàm số:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:
Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là
x1 < x2 f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là
x1 < x2 f(x1) > f(x2).
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.
- Nhận xét: Từ định nghĩa trên ta thấy:
a) f(x) đồng biến trên K
f(x) nghịch biến trên K
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.
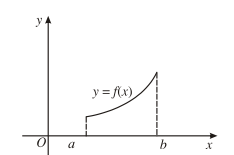
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.
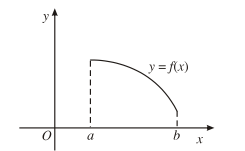
Tính đơn điệu và dấu của đạo hàm
- Định lí:
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
- Chú ý:
Nếu f’(x) = 0 với thì f(x) không đổi trên K.
Quy tắc xét tính đơn điệu của hàm số.
- Bước 1. Tìm tập xác định.
- Bước 2. Tính đạo hàm f’(x). Tìm các điểm xi ( i = 1; 2; …; n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.
Phần I. Các bài toán không chứa tham số.
Dạng 1: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị xi (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.
Bước 4. Sắp xếp các giá trị xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất.
Dạng 2: Từ bảng biến thiên, đồ thị hàm số của hàm số f’(x), xác định khoảng đồng biến, nghịch biến của hàm số đã cho.
- Dựa vào bảng biến thiên có sẵn, kết luận khoảng đồng biến, nghịch biến và chọn đáp án đúng.
- Từ đồ thị hàm số của hàm số f’(x), ta có:
+ Khoảng đồng biến của hàm số là khoảng mà tại đó giá trị f'(x) > 0 (nằm phía trên trục hoành).
+ Khoảng đồng biến của hàm số là khoảng mà tại đó f'(x) < 0 (nằm phía dưới trục hoành).
Xét bài toán: Cho bảng biến thiên của hàm số f’(x). Xét tính đồng biến, nghịch biến của hàm số g(x) theo f(x).
- Các bước giải:
Bước 1: Ta tính đạo hàm .
Bước 2: Kết hợp các nguyên tắc xét dấu tích, thương, tổng (hiệu) và bảng biến thiên của f’(x) để có được bảng xét dấu cho .
Bước 3: Dựa vào bảng xét dấu của vừa có để kết luận về sự đồng biến, nghịch biến của hàm số g(x).
Dạng 3. Xét sự đồng biến, nghịch biến của hàm hợp.
Bài toán 1: Cho hàm y = f(x) hoặc hàm y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x)).
Phương pháp:
- Tính đạo hàm
- Xét dấu dựa vào dấu của và theo quy tắc nhân dấu. Lưu ý khi xét dấu dựa vào dấu của như sau: Nếu không đổi dấu trên D thì không đổi dấu khi .
Bài toán 2: Cho hàm y = f(x) hoặc y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x))+h(x).
Phương pháp:
- Tính
- Lập bảng xét dấu bằng cách cộng dấu của hai biểu thức và .
Bài toán 3: Cho hàm y = f(u(x)) hoặc hàm y = f '(u(x)) xét sự biến thiên của hàm y = f(x).
Phương pháp: Giả sử ta có: . Ta cần giải BPT .
- Đặt
- Giải bất phương trình:
- Vậy .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2024 + Bài Tập) – Toán 12
50 bài tập về sự đồng biến và nghịch biến của hàm số (có đáp án 2024) – Toán 12
Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có đáp án 2024) - Toán 12
Đáp án đúng: B
*Lời giải
Hàm số y = f(x) đồng biến trên khoảng (−1; 2)⇒f'.
Xét hàm số .
Ta có .
Vậy hàm số y = f(x + 2) đồng biến trên khoảng (-3;0)* Lý thuyết cần nắm và một số dạng toán về sự đồng biến, nghịch biến của hàm số:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:
Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là
x1 < x2 f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là
x1 < x2 f(x1) > f(x2).
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.
- Nhận xét: Từ định nghĩa trên ta thấy:
a) f(x) đồng biến trên K
f(x) nghịch biến trên K
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.

Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.

Tính đơn điệu và dấu của đạo hàm
- Định lí:
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
- Chú ý:
Nếu f’(x) = 0 với thì f(x) không đổi trên K.
Quy tắc xét tính đơn điệu của hàm số.
- Bước 1. Tìm tập xác định.
- Bước 2. Tính đạo hàm f’(x). Tìm các điểm xi ( i = 1; 2; …; n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
- Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
- Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
CÁC DẠNG TOÁN THƯỜNG GẶP VÀ PHƯƠNG PHÁP GIẢI.
Phần I. Các bài toán không chứa tham số.
Dạng 1: Sử dụng đạo hàm để xác định khoảng đồng biến, nghịch biến của hàm số.
Bước 1. Tìm tập xác định D.
Bước 2. Tính đạo hàm y’ = f'(x). Tìm các giá trị xi (i=1, 2, .., n) mà tại đó f'(x) = 0 hoặc f'(x) không xác định.
Bước 4. Sắp xếp các giá trị xi theo thứ tự tăng dần và lập bảng biến thiên.
Bước 5. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số và chọn đáp án chính xác nhất.
Dạng 2: Từ bảng biến thiên, đồ thị hàm số của hàm số f’(x), xác định khoảng đồng biến, nghịch biến của hàm số đã cho.
- Dựa vào bảng biến thiên có sẵn, kết luận khoảng đồng biến, nghịch biến và chọn đáp án đúng.
- Từ đồ thị hàm số của hàm số f’(x), ta có:
+ Khoảng đồng biến của hàm số là khoảng mà tại đó giá trị f'(x) > 0 (nằm phía trên trục hoành).
+ Khoảng đồng biến của hàm số là khoảng mà tại đó f'(x) < 0 (nằm phía dưới trục hoành).
Xét bài toán: Cho bảng biến thiên của hàm số f’(x). Xét tính đồng biến, nghịch biến của hàm số g(x) theo f(x).
- Các bước giải:
Bước 1: Ta tính đạo hàm .
Bước 2: Kết hợp các nguyên tắc xét dấu tích, thương, tổng (hiệu) và bảng biến thiên của f’(x) để có được bảng xét dấu cho .
Bước 3: Dựa vào bảng xét dấu của vừa có để kết luận về sự đồng biến, nghịch biến của hàm số g(x).
Dạng 3. Xét sự đồng biến, nghịch biến của hàm hợp.
Bài toán 1: Cho hàm y = f(x) hoặc hàm y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x)).
Phương pháp:
- Tính đạo hàm
- Xét dấu dựa vào dấu của và theo quy tắc nhân dấu. Lưu ý khi xét dấu dựa vào dấu của như sau: Nếu không đổi dấu trên D thì không đổi dấu khi .
Bài toán 2: Cho hàm y = f(x) hoặc y = f '(x) xét sự biến thiên của hàm g(x) = f(u(x))+h(x).
Phương pháp:
- Tính
- Lập bảng xét dấu bằng cách cộng dấu của hai biểu thức và .
Bài toán 3: Cho hàm y = f(u(x)) hoặc hàm y = f '(u(x)) xét sự biến thiên của hàm y = f(x).
Phương pháp: Giả sử ta có: . Ta cần giải BPT .
- Đặt
- Giải bất phương trình:
- Vậy .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2024 + Bài Tập) – Toán 12
50 bài tập về sự đồng biến và nghịch biến của hàm số (có đáp án 2024) – Toán 12
Trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số (có đáp án 2024) - Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
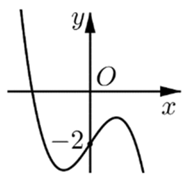
Cho hàm số bậc ba y = f(x) có đồ thị như hình bên. Hỏi phương trình (f(x))2 = 4 có bao nhiêu nghiệm thực?

Câu 2:
Cho hàm số y = f(x) có bảng biến thiên như sau:
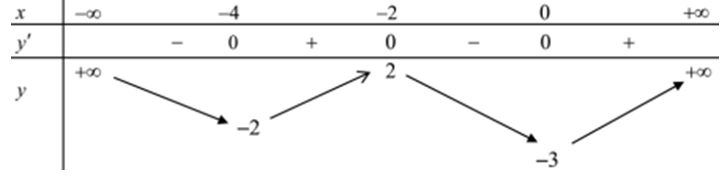
Có bao nhiêu giá trị nguyên của m để phương trình 4f(x2 - 4x) = m có ít nhất ba nghiệm dương phân biệt?
Cho hàm số y = f(x) có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của m để phương trình 4f(x2 - 4x) = m có ít nhất ba nghiệm dương phân biệt?
Câu 3:
Cho hàm số y = f(x) có đạo hàm trên R\{-1} và có bảng biến thiên như hình bên. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
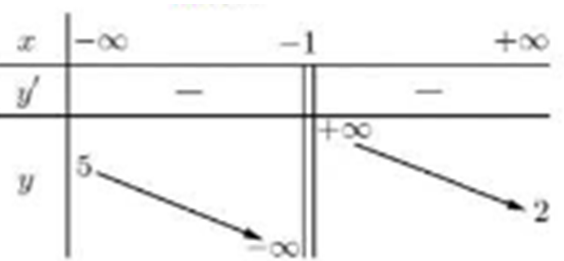
Cho hàm số y = f(x) có đạo hàm trên R\{-1} và có bảng biến thiên như hình bên. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là




![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)