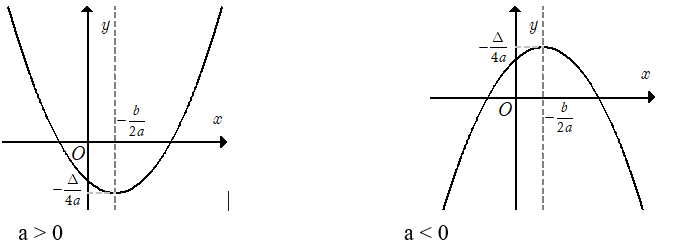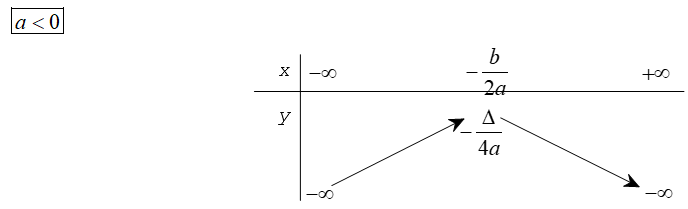Câu hỏi:
17/06/2026 215Hàm số nào dưới đây là hàm số bậc hai?
A. y = x4 + 3x2 + 2
B. y =
C = - 3x2 + 1
D. y =
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Lời giải:
Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + x với a, b, c là các hằng số và a ≠ 0.
Vậy trong các hàm số đã cho thì hàm số y = – 3x2 + 1 là hàm số bậc hai với các hệ số a = – 3, b = 0 và c = 1.
Chú ý: Hàm số không phải là hàm số bậc hai, mà đây là hàm số có thể đưa về dạng bậc hai nếu ta đặt .
* Kiến thức mở rộng
Hàm số bậc hai được cho bởi công thức
y = ax2 + bx + c (a ≠ 0).
Tập xác định của hàm số này là D = R
Hàm số y = ax2 (a ≠ 0) đã học ở lớp 9 là một trường hợp riêng của hàm số này.
I. ĐỒ THỊ CỦA HÀM SỐ BẬC HAI
Đồ thị của hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm I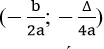
, có trục đối xứng là đường thẳng x = -
. Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
Cách vẽ
Để vẽ parabol y = ax2 + bx + c (a≠0) ta thực hiện các bước
1) Xác định tọa độ của đỉnh I
2) Vẽ trục đối xứng x = -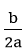
.
3) Xác định tọa độ các giao điểm của parabol với trục tung (điểm (0; c)) và trục hoành (nếu có).
Xác định thêm một số điểm thuộc đồ thị, chẳng hạn điểm đối xứng với điểm (0; c) qua trục đối xứng của parabol, để vẽ đồ thị chính xác hơn.
4) Vẽ parabol.
Khi vẽ parabol cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới).
II. CHIỀU BIẾN THIÊN CỦA HÀM SỐ BẬC HAI
Dựa vào đồ thị hàm số y = ax2 + bx + c (a≠0) ta có bảng biến thiên của nó trong hai trường hợp a > 0 và a < 0 như sau
Từ đó, ta có định lí dưới đây
Định lí
Nếu a < 0 thì hàm số y = ax2 + bx + c nghịch biến trên khoảng (–∞; -
); đồng biến trên khoảng (-; +∞).
Nếu a > 0 thì hàm số y = ax2 + bx + c đồng biến trên khoảng (–∞; -) nghịch biến trên khoảng (-; +∞).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
trong không gian oxyz mặt phẳng alpha x + 2y + 3z - 6 = 0 cắt trục tung tại điểm có tung độ bằng
Câu 5:
Cho a, b, c khác 0 thỏa a + b + c = 2025 và 1/a + 1/b + 1/c = 1/2025. chứng tỏ rằng 3 số a, b, c luôn có một số bằng 2025
Câu 7:
Câu 1 : tính -37 độ 45 phút 30 giây đổi sang thành bao nhiêu radian ?
Câu 2 : đổi 5,6 radian sang độ ?
Câu 9:
Một đoàn xe vận tải dự định điều số xe cùng loại để vận chuyển 40 tấn hàng. Lúc sắp khởi hành, đoàn xe được giao thêm 14 tấn nữa. do đó phải điều thêm 2 xe cùng loại và mỗi xe ban đầu phải chở thêm nửa tấn nữa. tính số xe phải điều theo dự định
Câu 12:
Cho nửa đường tròn tâm O đường kính BC và bán kính R. A là một điểm thay đổi trên nửa đường tròn sao cho AB > AC. Tia phân giác góc BAC cắt đường trung trực của BC tại D. Hạ DH và DK lần lượt vuông góc tới AB và AC.
a) Chứng minh tứ giác AHDK là một hình vuông.
b) Chứng minh bốn điểm A, B, C và D cùng nằm trên một đường tròn.
c, qua C kẻ đường thẳng song song với AB cắt AD tại E , qua E kẻ đường thẳng song song với AC cắt đường thẳng BD tại X . CMR X là điểm cố định
d, hạ AM vuông góc vơi BC . Tìm GTLN của tổng (2AM+MB)
Câu 13:
cho hình bình hành abcd và điểm m tùy ý đẳng thức nào sau đây đúng
Câu 14:
Tổng của một số thập phân và một số tự nhiên là 82,34. Khi thực hiện phép tính này, một bạn đã quên viết dấu phẩy của số thập phân nên đã cộng hai số tự nhiên và có kết quả là 1106. Hãy tìm số thập phân và số tự nhiên đã cho.
