Câu hỏi:
18/04/2025 26Giải phương trình sau: 1+sin2x+cos2x1+cot2x=√2sinx.sin2x
x=-π4+k2π,
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C
* Lời giải:
Xét phương trình:
(do )
Vậy nghiệm của phương trình là: .
* Phương pháp giải:
- Vận dụng các kiến thức và cách giải của các phương trình lượng giác cơ bản để giải tìm ra nghiệm
* Lý thuyết cần nắm và một số phương trình lượng giác thường gặp:
a) Phương trình bậc nhất đối với một hàm số lượng giác
* Phương pháp giải:
Chuyển vế rồi chia hai vế của phương trình dạng at+b=0 (1) cho a, ta đưa phương trình (1) về phương trình lượng giác cơ bản.
b) Phương trình bậc hai đối với một hàm số lượng giác
* Phương pháp giải:
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình theo ẩn phụ này. Cuối cùng ta đưa về việc giải các phương trình lượng giác cơ bản.
1. Hàm số y = sinx.
Từ định nghĩa ta thấy hàm số y = sinx :
+ Xác định với mọi x và – 1 ≤ sinx ≤ 1.
+ Là hàm số lẻ.
+ Là hàm số tuần hoàn với chu kì 2π.
Sau đây, ta sẽ khảo sát sự biến thiên của hàm số y = sinx.
a) Sự biến thiên và đồ thị hàm số y = sinx trên đoạn [0; π].
Hàm số y = sinx đồng biến trên và nghịch biến trên .
Bảng biến thiên:
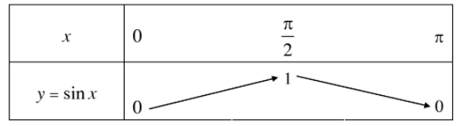
Đồ thị của hàm số y = sinx trên đoạn [0; π] đi qua các điểm (0; 0); (x1; sinx1); (x2; sinx2); (x3; sinx3); (x4; sinx4); (π; 0).
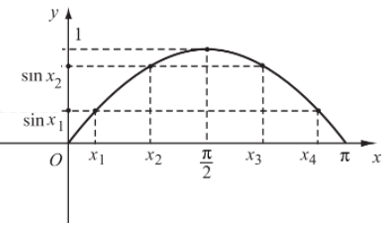
c) Tập giá trị của hàm số y = sinx
Tập giá trị của hàm số này là [– 1; 1].
2. Hàm số y = cosx.
Từ định nghĩa ta thấy hàm số y = cosx:
+ Xác định với mọi x và – 1 ≤ cosx ≤ 1.
+ Là hàm số chẵn.
+ Là hàm số tuần hoàn với chu kì 2π.
Với mọi x ta có: .
Từ đó, bằng cách tịnh tiến đồ thị hàm số y = sinx theo vecto (sang trái một đoạn có độ dài bằng , song song với trục hoành), ta được đồ thị hàm số y = cos x.
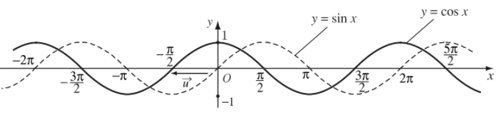
+ Hàm số y = cos x đồng biến trên đoạn [– π; 0] và nghịch biến trên đoạn [0; π].
+ Bảng biến thiên:
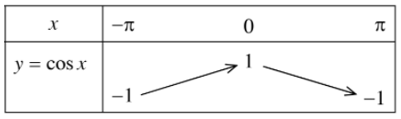
+ Tập giá trị của hàm số y = cosx là [– 1; 1].
+ Đồ thị của các hàm số y = cosx; y = sinx được gọi chung là các đường hình sin.
3. Hàm số y = tanx.
Từ định nghĩa hàm số y = tan x:
+ Có tập xác định: .
+ Là hàm số lẻ.
+ Là hàm số tuần hoàn với chu kì π.
Sự biến thiên và đồ thị hàm số y = tanx trên nửa khoảng
+ Hàm số y = tanx đồng biến trên nửa khoảng .
+ Bảng biến thiên:
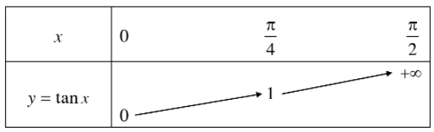
+ Bảng giá trị:
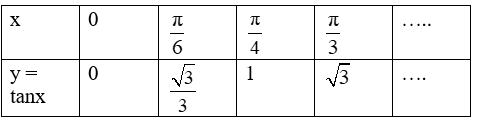
Đồ thị hàm số y = tanx trên nửa khoảng đi qua các điểm tìm được.
4. Hàm số y = cot x
Hàm số y = cotx:
+ Có tập xác định là .
+ Là hàm số lẻ.
+ Là hàm số tuần hoàn với chu kì π.
Sự biến thiên của hàm số y = cotx trên khoảng (0; π).
Hàm số y = cotx nghịch biến trên khoàn (0; π).
Bảng biến thiên:
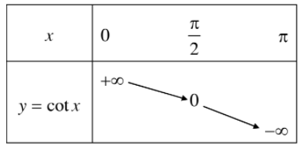
Hình biểu diễn của hàm số y = cotx trên khoảng (0; π).
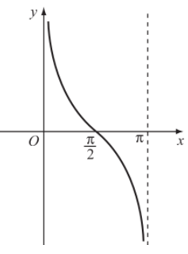
Xem thêm các bài viết liên quan hay, chi tiết:
Chuyên đề Phương trình lượng giác cơ bản - Toán 11
TOP 40 câu Trắc nghiệm Phương trình lượng giác cơ bản (có đáp án) – Toán 11
Trắc nghiệm Một số phương trình lượng giác thường gặp (có đáp án)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong hình bên, biết diện tích hình vuông là 16m2. Tính diện tích hình tròn tâm O.
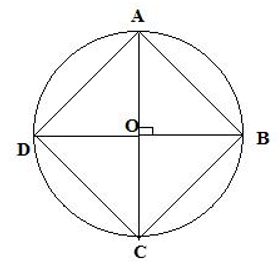
Câu 2:
Trên quãng đường AB, dài 210 km, tại cùng một thời điểm một xe máy khởi hành từ A đến B và một ô tô khởi hành từ B đến A. Sau khi gặp nhau, xe máy đi tiếp 4 giờ nữa thì đến B và ô tô đi tiếp 2 giờ 15 phút nữa thì đến A. Biết rằng vận tốc ô tô và xe máy không thay đổi trong suốt chặng đường. Vận tốc của xe máy và ô tô lần lượt là:
Câu 3:
Một tổ công nhân dự định làm xong 240 sản phẩm trong một thời gian nhất định. Nhưng khi thực hiện, nhờ cải tiến kĩ thuật nên mỗi ngày tổ đã làm tăng thêm 10 sản phẩm so với dự định. Do đó tổ đã hoàn thành sớm công việc sớm hơn dự định 2 ngày. Hỏi khi thực hiện, mỗi ngày tổ đã làm được bao nhiêu sản phẩm?
Câu 4:
Một ô tô, khối lượng là 4 tấn đang chuyển động đều trên con đường thẳng nằm ngang với vận tốc 10m/s, với công suất của động cơ ô tô là 20kW.
a. Tính hệ số ma sát giữa ô tô và mặt đường.
b. Sau đó ô tô tăng tốc, chuyển động nhanh dần đều và sau khi đi thêm được quãng đường 250m vận tốc ô tô tăng lên đến 54 km/h. Tính công suất trung bình của động cơ ô tô trên quãng đường này và công suất tức thời của động cơ ô tô ở cuối quãng đường. Lấy g = 10m/s2.
Câu 5:
Một người quan sát đứng cách một cái tháp 10m, nhìn thẳng đỉnh tháp và chân tháp lần lượt dưới 1 góc 550 và 100 so với phương ngang của mặt đất. Hãy tính chiều cao của tháp.
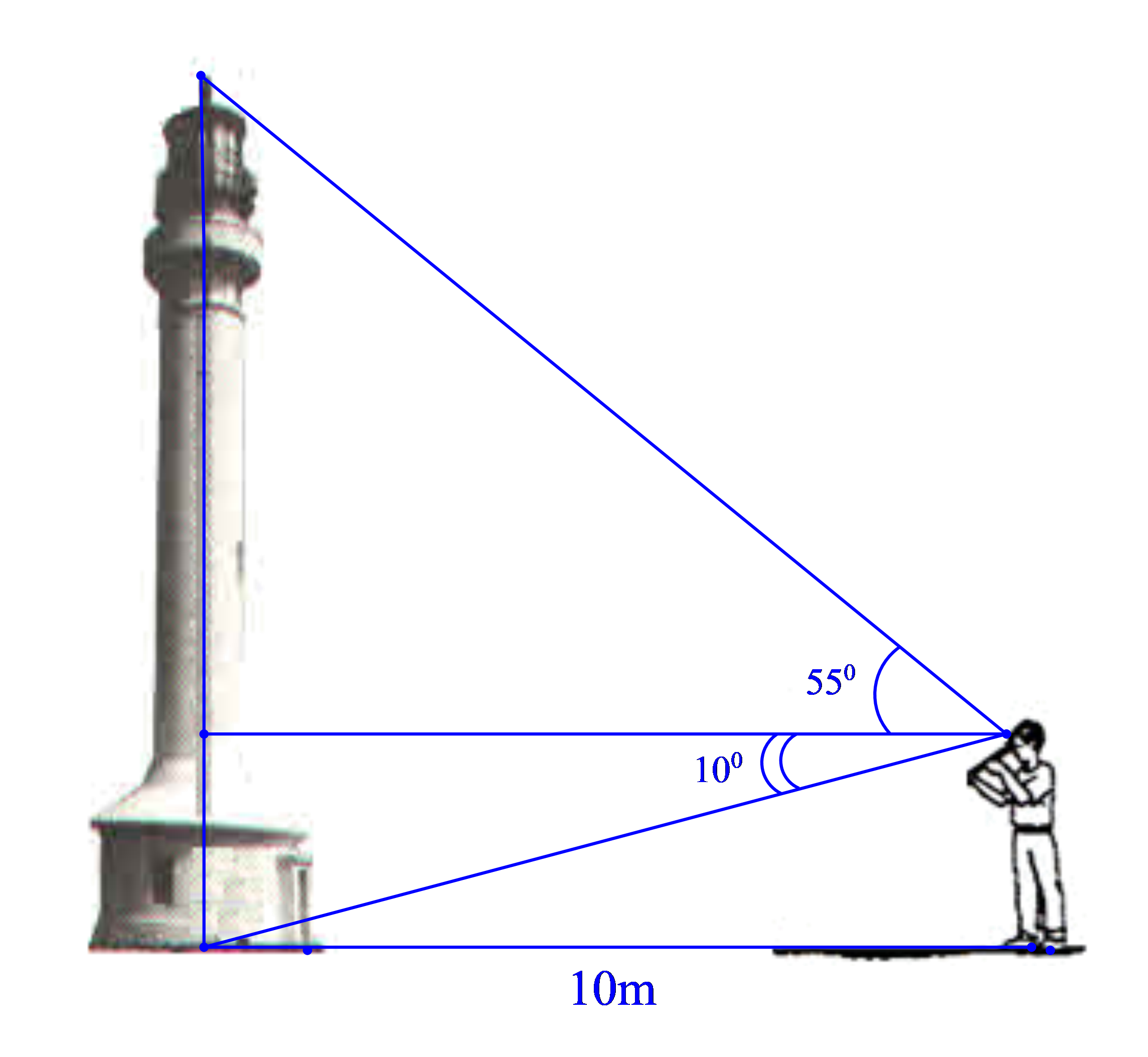

Câu 7:
Cho hình thoi ABCD, góc A = 60. Qua C kẻ đường thẳng d bất kì cắt các tia đối của các tia BA, DA theo thứ tự tại E và F. Gọi I là giao điểm của BF và ED. Chứng minh:
a)
b)
c)
Câu 8:
Cho phương trình log2(2x-1)2 = 2log2(x-2). Số nghiệm thực của phương trình là:
Câu 10:
Cho có . Tia phân giác của góc B cắt AC ở D, tia phân giác của góc C cắt AB ở E và cắt BD ở I. Chứng minh IE = ID
Câu 11:
Một nhóm công nhân gồm 15 nam và 5 nữ. Người ta muốn chọn từ nhóm ra 5 người để lập thành một tổ công tác sao cho phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nữ. Hỏi có bao nhiêu cách lập tổ công tác?
Câu 12:
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân, cạnh huyền bằng . Thể tích khối nón là:
Câu 13:
Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a, đáy ABC là tam giác vuông cân tại B và AC = . Tính thể tích V của khối lăng trụ đã cho.
Câu 14:
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn đều là nữ


