Câu hỏi:
27/11/2024 102Có bao nhiêu khối đa diện đều trong những khối dưới đây?
A. 1 khối
B. 2 khối
C. 3 khối
D. 4 khối.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B.
* Lời giải:
Hình 2 và Hình 5 là hình ảnh của khối bát diện đều và khối 12 mặt đều
* Phương pháp giải:
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}. Xem lại các mặt và đỉnh của từng loại khối đa diện
*Lý thuyến cần nắm và dạng toán về khối đa diện:
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
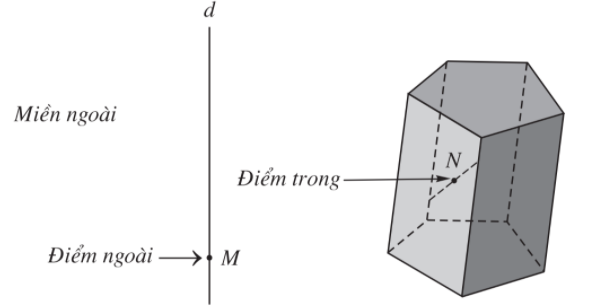
Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
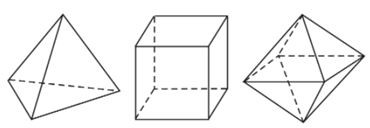
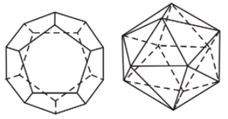
Bảng tóm tắt của năm loại khối đa diện đều.

Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khái niệm về khối đa diện (mới 2024 + Bài Tập) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+16=0 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)2=9. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là
Câu 2:
Cho tam giác OAB vuông cân tại O có AB = 2. Gọi H là trung điểm của AB. Tính diện tích xung quanh Sxq của hình nón sinh bởi quay tam giác OAB quanh OH
Câu 3:
Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính từ đấu mép dưới của màn hình). Để nìn rõ nhất phải xác định vị trí đứng cách màn ảnh sao cho góc nhìn lớn nhất
Vị trí đó cách màn ảnh
Câu 4:
Cho tam giác ABC có hai đỉnh B, C cố định BC = 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là
Câu 5:
Cho x, y, z là các số thực dương thỏa mãn điều kiện . Giá trị nhỏ nhất của biểu thức: nằm trong khoảng nào sau đây?
Câu 6:
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC vuông tại A(2;1), đường thẳng BC: 4x-3y+5=0. P là một điểm di động trên cạnh AC (P khác A và C). Đường tròn đường kính PC cắt BP tại I sao cho: BP.BI + CP.CA=25. Biết rằng B, C có tọa độ nguyên và C có hoành độ lớn hơn B. Hoành độ của điểm B là
Câu 7:
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B. C khác với gốc tọa độ sao cho biểu thức 6OA+3OB+2OC có giá trị nhỏ nhất
Câu 9:
Trong không gian Oxyz, cho hai đường thẳng và
Mệnh đề nào sau đây đúng?
Câu 10:
Cho hai điểm A(-1;2), B(3;1) và đường thẳng Điểm C(x;y) thuộc để tam giác ACB cân tại C. Giá trị x + y là
Câu 11:
Cho tam giác ABC đều cạnh a. Gọi (P) là mặt phẳng chứa BC và vuông góc với mặt phẳng (ABC). Trong (P) xét đường tròn (C) đường kính BC. Diện tích mặt cầu nội tiếp hình nón có đáy là (C) và đỉnh A bằng
Câu 12:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A và B phân biệt. Biết AB song song với mặt phẳng (zOx) và không song song với hai mặt phẳng (xOy), (yOz). Tọa độ của có thể là (với a,b#0)
Câu 13:
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng a3 .Gọi M là trung điểm của CC’. Tính khoảng cách từ điểm A’ đến mặt phẳng (ABM) biết rằng ABM là tam giác đều cạnh a
Câu 14:
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên hợp với mặt đáy một góc Tính thể tích của khối cầu tiếp hình chóp S.ABC
Câu 15:
Cho hàm số y=f(x) có đạo hàm f’(x)=(x-1)2(x2-2x) với mọi . Có bao nhiêu giá trị nguyên dương của tham số m để hàm y=f(x2-8x+m) có 5 điểm cực trị



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)