Lời giải

Áp dụng BĐT AM-GM với 3 số a, b, c ta luôn có:

$a+b\ge 2\sqrt{ab}$ , dấu bằng xảy ra khi a = b.

$b+c\ge 2\sqrt{bc}$ , dấu bằng xảy ra khi b = c.

$a+c\ge 2\sqrt{ac}$ , dấu bằng xảy ra khi a = c.

$\Rightarrow (a+b)(b+c)(c+a)\ge 2\sqrt{bc}.2\sqrt{ab}.2\sqrt{ac}=8abc$ 

Lại có: 

$(a+b)(b+c)(c+a)+abc=(a+b+c)(ab+bc+ca)\le (\frac{1}{8}+1)(a+b)(b+c)(c+a)$

$\iff (a+b+c)(ab+bc+ca)\le \frac{9}{8}(a+b)(b+c)(c+a)$

$\iff (a+b)(b+c)(c+a)\ge \frac{8}{9}(a+b+c)(ab+bc+ca)(đpcm)$

Dấu ''='' xảy ra khi $a=b=c$.

Vậy ta có BĐT cần Chứng minh.

*Phương pháp giải:

Áp dụng bất đẳng thức cosi

*Lý thuyết:

1. Bất đẳng thức Cô-si

Bất đẳng thức Cô-si là một trong những bất đẳng thức cổ điển. Tên chính xác là bất đẳng thức giữa trung bình cộng và trung bình nhân, nhiều người gọi là bất đẳng thức AM – GM (AM là viết tắt của Arithmetic mean và GM là viết tắt của Geometric mean). Do nhà toán học người Pháp Augustin – Louis Cauchy (1789 – 1857), người đã đưa ra một cách chừng mình đặc sắc nên nhiều người hay gọi là bất đẳng thức Cauchy.

2. Các dạng biểu diễn của bất đẳng thức Cô-si

a. Dạng tổng quát bất đẳng thức cosi

Cho x₁, x₂, x₃ ,…, x_n là các số thực không âm ta có:

Dạng 1: $\frac{x_1+x_2+...+x_n}{n }\ge \sqrt[n]{x_1.x_2...x_n}$

Dạng 2: x₁ + x₂ +...+x_n $\ge n.\sqrt[n]{x_1.x_2...x_n}$

Dạng 3: ${\left(\frac{x_{1 }+x_2+...+x_n}{n}\right)}^n\ge x_1.x_2...x_n$

Dấu đẳng thức xảy ra khi và chỉ khi x₁ = x₂ =....= x_n

Cho x₁, x₂, x₃ ,…, x_n là các số thực dương ta có:

Dạng 1:_{$\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n}\ge \frac{n^2}{x_1+x_2+...+x_n}$}

Dạng 2: (x₁ + x₂ + ... + xn) $(\frac{1}{x_1}+\frac{1}{x_2}+...+\frac{1}{x_n})\ge n^2$

b) Các bất đẳng thức côsi đặc biệt

c) Một số bất đẳng thức được suy ra từ bất đẳng thức Cô si

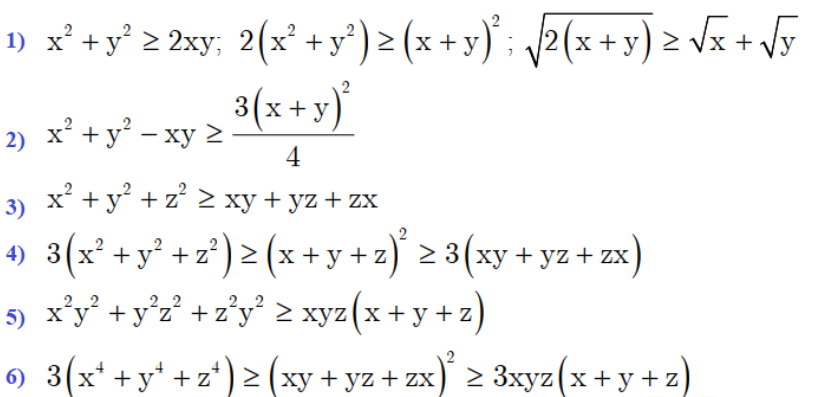
d) Chú ý khi sử dụng bất đẳng thức AM – GM

• Khi áp dụng bất đẳng thức cô si thì các số phải là những số không âm
• Bất đẳng thức côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích
• Điều kiện xảy ra dấu ‘=’ là các số bằng nhau
• Bất đẳng thức côsi còn có hình thức khác thường hay sử dụng

Xem thêm

Áp dụng bất đẳng thức Cô - si, tìm GTLN - GTNN của biểu thức ( + Bài tập)