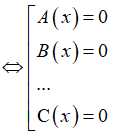Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
*Phương pháp giải:
Giải phương trình tích: Cho phương trình A(x).B(x)...C(x) = 0 (1), trong đó A(x).B(x)...C(x) là các phương trình ẩn x.
Bước 1: Biến đổi tương đương A(x).B(x)...C(x) = 0
Bước 2: Lần lượt giải các phương trình A(x) = 0; B(x) = 0;... C(x) = 0.
Bước 3: Kết luận.
*Lý thuyết:
- Phương trình bậc hai có dạng ax2+bx+c=0 (a≠0)
- Cách giải và biện luận phương trình bậc hai:
+ Với Δ=b2−4ac
Nếu Δ>0 thì phương trình bậc hai có hai nghiệm phân biệt:
x1=−b+√Δ2a,x2=−b−√Δ2a
Nếu Δ=0 thì phương trình bậc hai có nghiệm kép: x1=x2=−b2a
Nếu Δ<0 thì phương trình bậc hai vô nghiệm.
+ Với Δ' với
Nếu thì phương trình bậc hai có hai nghiệm phân biệt:
,
Nếu thì phương trình bậc hai có nghiệm kép:
Nếu thì phương trình bậc hai vô nghiệm.
- Đối với các phương trình quy về phương trình bậc hai ta có thể dùng các phép biến đổi như nhân đa thức, quy đồng mẫu số, chuyển vế, lấy nhân tử chung … để đưa phương trình đã cho về dạng ().
Xem thêm