Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OC = 2a, OA = OB = a. Gọi M là trung điểm của AB. Tính khoảng cách giữa hai đường thẳng OM và AC

Đáp án đúng: A

*Lời giải

*Phương pháp giải

-  áp dụng công thức tính khoảng cách giữa đường thẳng và mặt phẳng 

*Lý thuyến cần nắm và các dạng bài toán về khoảng cách: 

Khoảng cách từ một điểm đến một đường thẳng

Cho điểm O và đường thẳng a. Trong mặt phẳng (O; a), gọi H là hình chiếu vuông góc của O lên a. Khi đó, khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a.

Kí hiệu: d(O; a).

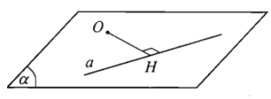
Khoảng cách từ một điểm đến một mặt phẳng

Cho điểm O và mặt phẳng (α). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (α). Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (α) và được kí hiệu là d(O; (α)).

 

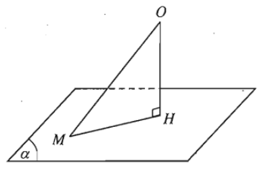
Khoảng cách giữa đường thẳng và măt phẳng song song.

- Định nghĩa: Cho đường thẳng a song song với mặt phẳng (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì thuộc a đến mặt phẳng (α).

Kí hiệu là d(a; (α)) .

 

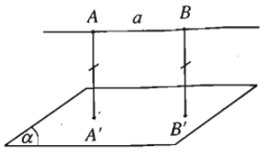
 Khoảng cách giữa hai mặt phẳng song song.

 Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

- Kí hiệu: d((α); (β)).

Như vậy: d((α); (β)) = d(M; (β)) = d(M’; (α)).

 

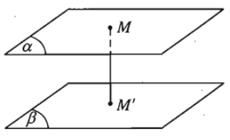
Cách tìm đường vuông góc chung của hai đường thẳng chéo nhau.

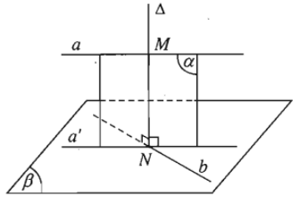
- Cho hai đường thẳng chéo nhau a và b. Gọi (β) là mặt phẳng chứa b và song song với a; a’ là hình chiếu vuông góc của a trên mặt phẳng (β).

Vì a// (β) nên a// a’. Do đó; a’ cắt b tại 1 điểm là N

Gọi (α) là mặt phẳng chứa a và a’; ∆ là đường thẳng đi qua N và vuông góc với (β). Khi đó, (α) vuông góc (β).

Như vậy.∆ nằm trong (α) nên cắt đường thẳng a tại M và cắt đường thẳng b tại N.Đồng thời, ∆ vuông góc với cả a và b.

Do đó, ∆ là đường vuông góc chung của a và b.

 

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Khoảng cách (mới + Bài Tập) - Toán 11 

Sách bài tập Toán 11 (Kết nối tri thức): Bài tập cuối chương 7