50 câu hỏi trắc nghiệm thuộc Bộ đề luyện thi thpt quốc gia môn Toán cực hay có lời giải (Đề số 4)

Cosin góc tạo bởi cạnh bên và mặt đáy của hình chóp tứ giác đều có tất cả các cạnh bằng nhau là

A. $\frac{1}{3} .$

B. $\frac{1}{\sqrt{3}} .$

C. $\frac{\sqrt{3}}{2} .$

D. $\frac{1}{\sqrt{2}} .$

Xem đáp án

Câu 2:

16/07/2024

Điều kiện xác định của phương trình $\sqrt{x - 2} + \frac{6}{x - 3} = 4$ là tập nào sau đây?

A. $R \ \{3\} .$

B. $[2; + \infty) .$

C.R

D. $[2; + \infty) \ \{3\} .$

Xem đáp án

Câu 3:

Cho M là trung điểm của đoạn AB. Khẳng định nào sau đây đúng?

A. $\vec{I A} + \vec{I B} = \vec{A B}$ với I là điểm bất kì

B. $\vec{A M} + \vec{B M} = \vec{0} .$

C. $\vec{I A} + \vec{I B} = \vec{I M}$ với I là điểm bất kì.

D. $\vec{A M} + \vec{M B} = \vec{0} .$

Xem đáp án

Câu 4:

Trong các hàm số sau hàm số nào nghịch biến trên R ?

A. $y = \log_{3} x^{2} .$

B. $y = {(\frac{e}{4})}^{x} .$

C. $y = \log (x^{3}) .$

D. $y = {(\frac{π}{4})}^{- x} .$

Xem đáp án

Câu 5:

Véc tơ nào trong các véc tơ dưới đây là véc tơ pháp tuyến của đường thẳng $y + 2 x - 1 = 0 ?$

A.(2;-1)

B(1;2)

C.(-2;1)

D.(-2;-1)

Xem đáp án

Câu 6:

Cho lăng trụ tam giác ABC.A'B'C' , biết thể tích lăng trụ là V. Tính thể tích khối chóp C.ABB'A' ?

A. $\frac{2}{3} V .$

B. $\frac{1}{3} V .$

C. $\frac{3}{4} V .$

D. $\frac{1}{2} V .$

Xem đáp án

Câu 7:

Tìm số điểm cực trị của đồ thị hàm số $y = \frac{x - 2}{x + 1}$ ?

A.4

B.1

C.0

D.3

Xem đáp án

Câu 8:

Dãy số nào sau đây là cấp số cộng?

A. $(u_{n}) : u_{n} = \frac{1}{n} .$

B. $(u_{n}) : u_{n} = u_{n - 1} - 2, \forall n \geq 2 .$

C. $(u_{n}) : u_{n} = 2^{n} - 1 .$

D. $(u_{n}) : u_{n} = 2 u_{n - 1}, \forall n \geq 2 .$

Xem đáp án

Câu 9:

Đạo hàm của hàm số $y = \ln (\sqrt{x^{2} + 1} - x)$ là

A. $\frac{1}{\sqrt{x^{2} + 1}} .$

B. $\frac{1}{\sqrt{x^{2} + 1} - x} .$

C. $\frac{1}{\sqrt{x^{2} + 1} + x} .$

D. $\frac{- 1}{\sqrt{x^{2} + 1}} .$

Xem đáp án

Câu 10:

Tập hợp tất cả các số thực x thỏa mãn ${(\frac{2}{3})}^{4 x} \leq {(\frac{3}{2})}^{2 - x}$ là

A. $[\frac{- 2}{3}; + \infty) .$

B. $[\frac{5}{2}; + \infty) .$

C. $(- \infty; \frac{2}{5}] .$

D. $(- \infty; \frac{2}{3}] .$

Xem đáp án

Câu 11:

Tập xác định của hàm số $y = \log_{2} x .$

A. $(0; + \infty) .$

B. $[0; + \infty) .$

C. $R \ \{0\} .$

D.R

Xem đáp án

Câu 12:

Cho hàm số y=f(x) có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $(- 1; + \infty) .$

B.(-1;1)

C. $(- \infty; 1) .$

D. $(1; + \infty) .$

Xem đáp án

Chọn D

Câu 13:

Cho A là tập hợp khác $\emptyset (\emptyset$ là tập hợp rỗng). Xác định mệnh đề đúng trong các mệnh đề sau

A. $\emptyset \in A .$

B. $A \cap \emptyset = A .$

C. $\emptyset \subset A .$

D. $A \cup \emptyset = \emptyset .$

Xem đáp án

Chọn C.

Câu 14:

20/07/2024

Khẳng định nào sai trong các khẳng định sau?

A.y=cosx tuần hoàn với chu kỳ $π .$

B.y=cosx nghịch biến trên khoảng $(0; π .)$

C.y=cosx là hàm chẵn

D.y=cosx có tập xác định là R

Xem đáp án

Câu 15:

19/07/2024

Số cách chọn ra ba bạn bất kỳ từ một lớp có 30 bạn là

A. $C_{30}^{3} .$

B. $\frac{A_{30}^{3}}{3} .$

C. $3! . A_{30}^{3} .$

D. $A_{30}^{3} .$

Xem đáp án

Chọn A

Câu 16:

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = - x^{4} + 2 x^{2} - 1$ trên đoạn [-2;1]. Tính M + m

A.0

B.-9

C.-10

D.-1

Xem đáp án

Câu 17:

18/07/2024

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, biết $V_{S . A B C D} = \frac{a^{3}}{3 \sqrt{3}} .$ Tính góc giữa SA và mặt phẳng (SCD).

A. $60^{0} .$

B. $45^{0} .$

C. $30^{0} .$

D. $90^{0} .$

Xem đáp án

Câu 18:

17/07/2024

Số nghiệm thuộc đoạn $[0; 2018 π]$ của phương trình cos2x-2xinx+3=0 là

A.2017

B.1009

C.1010

D.2018

Xem đáp án

Câu 19:

Tìm m để hệ phương trình $\{\begin{cases} m x - 2 y = 1 \\ 2 x + y = 2 \end{cases}$ có nghiệm.

A. $m \neq 4 .$

B. $m \neq - 2 .$

C. $m \neq 2 .$

D. $m \neq - 4 .$

Xem đáp án

Câu 20:

15/07/2024

Cho a, b, c là các số thực dương và khác 1. Hình vẽ bên là đồ thị của hàm số $y = \log_{a} x, y = \log_{b} x, y = \log_{c} x .$ Khẳng định nào sau đây là đúng?

A.b<c<a

B.b<a<c

C.a<b<c

D.c<a<b

Xem đáp án

Câu 21:

Tìm m để hàm số $y = \{\begin{cases} \frac{2 \sqrt[3]{x} - x - 1}{x - 1} khix \neq 1 \\ mx + 1 khix = 1 \end{cases}$ liên tục trên R

A. $- \frac{4}{3} .$

B. $- \frac{1}{3} .$

C. $\frac{4}{3} .$

D. $\frac{2}{3} .$

Xem đáp án

Câu 22:

19/07/2024

Gọi d là tiếp tuyến tại điểm cực đại của đồ thị hàm số $y = x^{4} - 3 x^{2} + 2 .$ Mệnh đề nào dưới đây đúng?

A.d có hệ số góc âm.

B.d song song với đường thẳng x = 3

C.d có hệ số góc dương

D.d song song với đường thẳng y = 3

Xem đáp án

Chọn D.

Điểm cực đại của đồ thị hàm số là A(0;2).

Phương trình tiếp tuyến tại A(0;2) là y = 2 (d).

Vậy d song song với đường thẳng y =3.

Câu 23:

Trong các mệnh đề sau, mệnh đề nào sai?

A.Hàm số $y = \ln (x + \sqrt{x^{2} + 1})$ là hàm số chẵn

B.Tập giá trị của hàm số $y = \ln (x^{2} + 1)$ là $[0; + \infty) .$

C.Hàm số $y = \ln (\sqrt{x^{2} + 1} - x)$ có tập xác định là R

D. $[\ln (x + \sqrt{x^{2} + 1})] = \frac{1}{\sqrt{x^{2} + 1}} .$

Xem đáp án

Câu 24:

Lý thuyết Khoảng cách (mới + Bài Tập) - Toán 11

Giá trị của m để phương trình có ba nghiệm phân biệt lập thành một cấp số cộng $x^{3} - 3 x^{2} + x - m = 0$ thuộc khoảng nào trong các khoảng dưới đây?

A.(2;4)

B.(-2;0)

C.(0;2)

D.(-4;2)

Xem đáp án

Câu 25:

01/11/2024

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OC = 2a, OA = OB = a. Gọi M là trung điểm của AB. Tính khoảng cách giữa hai đường thẳng OM và AC

A. $\frac{2 a}{3} .$

B. $\frac{2 \sqrt{5} a}{5} .$

C. $\frac{\sqrt{2} a}{3} .$

D. $\frac{\sqrt{2} a}{2} .$

Xem đáp án

Đáp án đúng: A

*Lời giải

*Phương pháp giải

- áp dụng công thức tính khoảng cách giữa đường thẳng và mặt phẳng

*Lý thuyến cần nắm và các dạng bài toán về khoảng cách:

Khoảng cách từ một điểm đến một đường thẳng

Cho điểm O và đường thẳng a. Trong mặt phẳng (O; a), gọi H là hình chiếu vuông góc của O lên a. Khi đó, khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến đường thẳng a.

Kí hiệu: d(O; a).

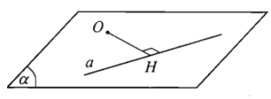
Khoảng cách từ một điểm đến một mặt phẳng

Cho điểm O và mặt phẳng (α). Gọi H là hình chiếu vuông góc của O lên mặt phẳng (α). Khi đó khoảng cách giữa hai điểm O và H được gọi là khoảng cách từ điểm O đến mặt phẳng (α) và được kí hiệu là d(O; (α)).

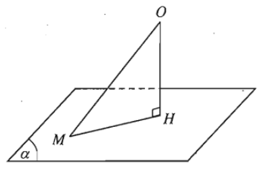
Khoảng cách giữa đường thẳng và măt phẳng song song.

- Định nghĩa: Cho đường thẳng a song song với mặt phẳng (α). Khoảng cách giữa đường thẳng a và mặt phẳng (α) là khoảng cách từ một điểm bất kì thuộc a đến mặt phẳng (α).

Kí hiệu là d(a; (α)) .

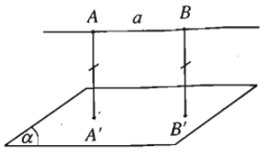
Khoảng cách giữa hai mặt phẳng song song.

Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng này đến mặt phẳng kia.

- Kí hiệu: d((α); (β)).

Như vậy: d((α); (β)) = d(M; (β)) = d(M’; (α)).

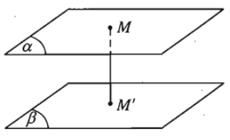
Cách tìm đường vuông góc chung của hai đường thẳng chéo nhau.

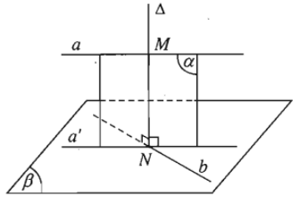
- Cho hai đường thẳng chéo nhau a và b. Gọi (β) là mặt phẳng chứa b và song song với a; a’ là hình chiếu vuông góc của a trên mặt phẳng (β).

Vì a// (β) nên a// a’. Do đó; a’ cắt b tại 1 điểm là N

Gọi (α) là mặt phẳng chứa a và a’; ∆ là đường thẳng đi qua N và vuông góc với (β). Khi đó, (α) vuông góc (β).

Như vậy.∆ nằm trong (α) nên cắt đường thẳng a tại M và cắt đường thẳng b tại N.Đồng thời, ∆ vuông góc với cả a và b.

Do đó, ∆ là đường vuông góc chung của a và b.

Xem thêm các bài viết liên quan hay, chi tiết:

Sách bài tập Toán 11 (Kết nối tri thức): Bài tập cuối chương 7

Câu 26:

Tìm tập xác định của hàm số $f (x) = \log_{2} \frac{x + \sqrt{x} - 2}{x - 2} .$

A. $R^{+} \ \{2\} .$

B. $[0; 1) \cup (2; + \infty) .$

C. $(2; + \infty) .$

D. $[0; + \infty) \ \{2\} .$

Xem đáp án

Câu 27:

Một nhóm học sinh gồm 5 bạn nam, và 3 bạn nữ cùng đi xem phim, có bao nhiêu cách xếp 8 bạn vào 8 ghế hàng ngang sao cho 3 bạn nữ ngồi cạnh nhau?

A.5!.3!

B. 8! – 5.3!.

C.6!.3!.

D. $\frac{8!}{3!} .$

Xem đáp án

Chọn C.

Ta coi 3 bạn nữ là vị trí thì số cách sắp xếp 6 là 6!, sau đó xếp 3 bạn nữ vào vị trí đó là 3! Nên số cách sắp xếp là 6!.3!

Câu 28:

Tính thể tích của khối bát diện đều có tất cả các cạnh bằng 2a

A. $\frac{\sqrt{2}}{6} a^{3} .$

B. $\frac{4 \sqrt{2}}{3} a^{3} .$

C. $\frac{8 \sqrt{2}}{3} a^{3} .$

D. $\frac{2 \sqrt{2}}{3} a^{3} .$

Xem đáp án

Câu 29:

Cho hàm số $y = a x^{3} + b x^{2} + c x + d$ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

A. $a < 0, b < 0, c < 0, d > 0 .$

B. $a > 0, b > 0, c < 0, d > 0 .$

C. $a > 0, b < 0, c < 0, d > 0 .$

D. $a > 0, b < 0, c > 0, d > 0 .$

Xem đáp án

Câu 30:

15/07/2024

Tìm số đường tiệm cận đứng của đồ thị hàm số $y = \frac{\sqrt{x + 9} - 3}{x^{2} + x} .$

A.3

B.1

C.0

D.2

Xem đáp án

Câu 31:

Cho hình lập phương ABCD.A'B'C'D' có tất cả các cạnh bằng 1. Gọi M là trung điểm của BB' .Tính thể tích khối A'MCD

A. $\frac{1}{12} .$

B. $\frac{2}{15} .$

C. $\frac{4}{15} .$

D. $\frac{1}{28} .$

Xem đáp án

Câu 32:

Với $a = \log_{2} 7, b = \log_{5} 7 .$ Tính giá trị của $\log_{10} 7 .$

A. $\frac{a b}{a + b} .$

B. $\frac{1}{a + b} .$

C.a+b

D. $\frac{a + b}{a b} .$

Xem đáp án

Câu 33:

20/07/2024

Một cái phễu có dạng hình nón, chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng 10 cm. Nếu bịt kín miệng phễu và lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng nhất với giá trị nào sau đây

A.1,07 cm

B.10cm

C.9,35cm

D.0,87cm

Xem đáp án

Câu 34:

Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm tất cả các giá trị của m để phương trình $f (4 x - x^{2}) = \log_{2} m$ có 4 nghiệm thực phân biệt

A. $m \in (0; 8) .$

B. $m \in (\frac{1}{2}; 8) .$

C. $m \in (- 1; 3) .$

D. $m \in (0; \frac{1}{2}) .$

Xem đáp án

Câu 35:

Tập tất cả các giá trị của m để phương trình $2 x \sqrt{1 - x^{2}} - m (x + \sqrt{1 - x^{2}}) + m + 1 = 0$ không có nghiệm thực là tập (a;b). Khi đó

A. $a - b = 2 + 2 \sqrt{2} .$

B. $a - b = - 2 - 2 \sqrt{2} .$

C. $a - b = \sqrt{2} .$

D. $a - b = - 2 \sqrt{2} .$

Xem đáp án

Câu 36:

Gọi S là tập nghiệm của phương trình $\log_{\sqrt{2}} {(x - 1)}^{3} - \log_{2} {(x - 3)}^{2} = 2 \log_{2} (x - 1)$ trên R Tìm số phần tử của S

A.1

B.3

C.4

D.2

Xem đáp án

Câu 37:

Tính tổng của tất cả các số có 5 chữ số đôi một khác nhau được lập thành từ tập $A = \{1; 2; 3; 4; 5\} .$

A.333.330

B. 7.999.920.

C.1.599.984.

D. 3.999.960.

Xem đáp án

Câu 38:

Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các nghiệm của phương trình $\cos^{2} x + 3 \sin x . \cos x = 1 .$

A. $\sqrt{3} .$

B. $\frac{3 \sqrt{10}}{10} .$

C. $\frac{3 \sqrt{10}}{5} .$

D. $\sqrt{2} .$

Xem đáp án

Câu 39:

19/07/2024

Tìm tất cả các giá trị của m để hàm số $y = \frac{m x + 16}{x + m}$ đồng biến trên $(0; + \infty)$ ?

A. $m \in (- \infty; - 4) .$

B. $m \in (- \infty; - 4) \cup (4; + \infty) .$

C. $m \in [4; + \infty) .$

D. $m \in (4; + \infty) .$

Xem đáp án

Câu 40:

Cho tam giác ABC vuông tại A, điểm M thuộc cạnh AC sao cho AB = 2AM, đường tròn tâm I đường kính CM cắt BM tại D, đường thẳng CD có phương trình x-3y-6=0 Biết I(1;-1), điểm $E (\frac{4}{3}; 0)$ thuộc đường thẳng BC, $x_{C} \in Z$ Biết điểm B có tọa độ (a;b). Khi đó:

A.a+b=1

B.a+b=0

C.a+b=-1

D.a+b=2

Xem đáp án

Câu 41:

Quay hình chữ nhật ABCD quanh trục AB cố định, đường gấp khúc ADBC cho ta hình trụ (T). Gọi $Δ M N P$ là tam giác đều nội tiếp đường tròn đáy (không chứa điểm A). Tính tỷ số giữa thể tích khối trụ và thể tích khối chóp A.MNP.

A. $\frac{4}{3 \sqrt{3}} π .$

B. $\frac{4}{\sqrt{3}} π .$

C. $\frac{\sqrt{3}}{4} π .$

D. $\frac{4}{3} π .$

Xem đáp án

Câu 42:

Một người mua một căn hộ với giá 900 triều đồng. Người đó trả trước với số tiền là 500 triệu đồng. Số tiền còn lại người đó thanh toán theo hình thức trả góp với lãi suất tính trên tổng số tiền còn nợ là 0,5% mỗi tháng. Kể từ ngày mua, sau đúng mỗi tháng người đó trả số tiền cố định là 4 triệu đồng (cả gốc lẫn lãi). Tìm thời gian (làm tròn đến hàng đơn vị) để người đó trả hết nợ

A.133 tháng

B.139 tháng

C.136 tháng

D.140 tháng

Xem đáp án

Câu 43:

Một con châu chấu nhảy từ gốc tọa độ đến điểm có tọa độ là A(9;0) dọc theo trục Ox của hệ trục tọa độ Oxy. Hỏi con châu chấu có bao nhiêu cách nhảy để đến điểm A, biết mỗi lần nó có thể nhảy 1 bước hoặc 2 bước (1 bước có độ dài 1 đơn vị).

A.47

B.51

C.55

D.54

Xem đáp án

Câu 44:

Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi E, F lần lượt là trung điểm các cạnh SB, SC. Biết mặt phẳng (AEF) vuông góc với mặt phẳng (SBC).

Thể tích của khối chóp S.ABC

A. $\frac{a^{3} \sqrt{5}}{8} .$

B. $\frac{a^{3} \sqrt{5}}{24} .$

C. $\frac{a^{3} \sqrt{6}}{12} .$

D. $\frac{a^{3} \sqrt{3}}{24} .$

Xem đáp án

Câu 45:

17/07/2024

Cho hình chóp đều S.ABC có $A B = a, \hat{A S B} = 30^{0} .$ Lấy các điểm B',C' lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác AB'C' nhỏ nhất. Tính chu vi đó

A. $(\sqrt{3} - 1) a .$

B. $\sqrt{3} a .$

C. $\frac{a}{1 + \sqrt{3}} .$

D. $(1 + \sqrt{3}) a .$

Xem đáp án

Câu 46:

18/07/2024

Cho hàm số y=f(x) có đúng ba điểm cực trị là 0; 1; 2 và có đạo hàm liên tục trên R. Khi đó hàm số $y = f (4 x - 4 x^{2})$ có bao nhiêu điểm cực trị?

A.5

B.2

C.3

D.4

Xem đáp án

Câu 47:

15/07/2024

Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai mặt phẳng (A'B'C) và (C'D'A)

A. $45^{0} .$

B. $30^{0} .$

C. $60^{0} .$

D. $90^{0} .$

Xem đáp án

Câu 48:

23/07/2024

Điểm nằm trên đường tròn $(C) : x^{2} + y^{2} - 2 x + 4 y + 1 = 0$ có khoảng cách ngắn nhất đến đường thẳng d:x-y+3=0 có tọa độ M(a;b). Khẳng định nào sau đây là đúng?

A. $\sqrt{2} a = - b .$

B.a=-b

C. $\sqrt{2} a = b .$

D.a=b

Xem đáp án

Câu 49:

17/07/2024

Cho m, n là các số nguyên dương khác 1. Gọi P là tích các nghiệm của phương trình $2018 (\log_{m} x) (\log_{n} x) = 2017 \log_{m} x + 2018 \log_{n} x + 2019 .$ P nguyên và đạt giá trị nhỏ nhất khi:

A. $m . n = 2^{2020} .$

B. $m . n = 2^{2017} .$

C. $m . n = 2^{2019} .$

D. $m . n = 2^{2018} .$

Xem đáp án

Câu 50: