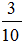Câu hỏi:
18/04/2025 15Cho tam giác ABC có a = 10, . Tính R, b, c.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải:
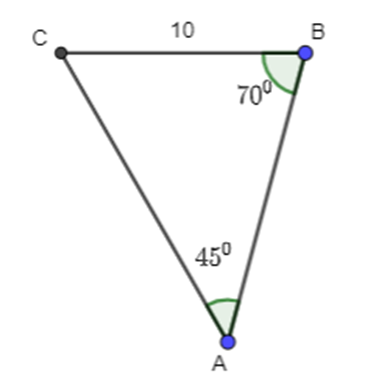
Xét ΔABC, có:
asinA=bsinB⇔b=a.sinBsinA=10sin700sin450≈13,29 (định lí sin)
Ta lại có: asinA=2R⇔R=a2sinA=102sin450=5√2.
Ta có: ˆC=1800−ˆA−ˆB=1800−450−700=650.
asinA=csinC⇔c=a.sinCsinA=10sin650sin450≈12,82.
Vậy R=5√2, b = 13,29, c = 12,82.
* Phương pháp giải:
Áp dụng hệ thức lượng trong tam giác để tính
* Một số dạng bài về hệ thức lượng trong tam giác:
Mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Đối với hai góc bù nhau, α và 180° – α, ta có:
sin (180° – α) = sin α;
cos (180° – α) = – cos α;
tan (180° – α) = – tan α (α ≠ 90°);
cot (180° – α) = – cot α (0° < α < 180°).
Định lí côsin
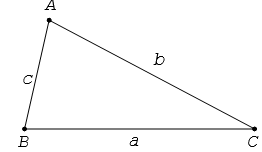
Cho tam giác ABC có BC = a, AC = b và AB = c:
a2 = b2 + c2 – 2bc.cosA; b2 = c2 + a2 – 2ca.cosB; c2 = a2 + b2 – 2ab.cosC.
Hệ quả
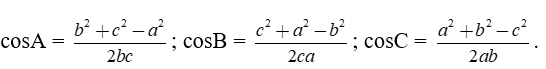
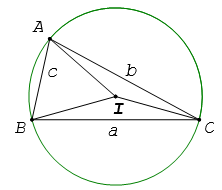
Định lí sin
Cho tam giác ABC có BC = a, AC = b, AB = c và R là bán kính đường tròn ngoại tiếp.
Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
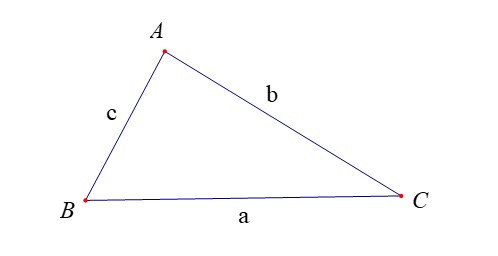
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
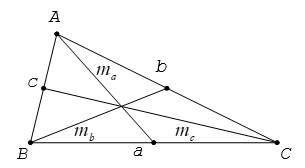
Độ dài đường trung tuyến
Cho tam giác ABC có ma, mb, mc lần lượt là các trung tuyến kẻ từ A, B, C.
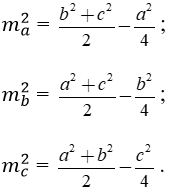
Xem thêm các bài viết liên quan hay, chi tiết
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình thoi ABCD, góc A = 60. Qua C kẻ đường thẳng d bất kì cắt các tia đối của các tia BA, DA theo thứ tự tại E và F. Gọi I là giao điểm của BF và ED. Chứng minh:
a)
b)
c)
Câu 2:
Một ô tô, khối lượng là 4 tấn đang chuyển động đều trên con đường thẳng nằm ngang với vận tốc 10m/s, với công suất của động cơ ô tô là 20kW.
a. Tính hệ số ma sát giữa ô tô và mặt đường.
b. Sau đó ô tô tăng tốc, chuyển động nhanh dần đều và sau khi đi thêm được quãng đường 250m vận tốc ô tô tăng lên đến 54 km/h. Tính công suất trung bình của động cơ ô tô trên quãng đường này và công suất tức thời của động cơ ô tô ở cuối quãng đường. Lấy g = 10m/s2.
Câu 3:
Một tổ công nhân dự định làm xong 240 sản phẩm trong một thời gian nhất định. Nhưng khi thực hiện, nhờ cải tiến kĩ thuật nên mỗi ngày tổ đã làm tăng thêm 10 sản phẩm so với dự định. Do đó tổ đã hoàn thành sớm công việc sớm hơn dự định 2 ngày. Hỏi khi thực hiện, mỗi ngày tổ đã làm được bao nhiêu sản phẩm?
Câu 4:
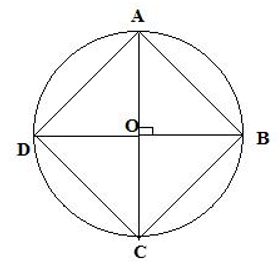
Trong hình bên, biết diện tích hình vuông là 16m2. Tính diện tích hình tròn tâm O.
Câu 5:
Cho phương trình log2(2x-1)2 = 2log2(x-2). Số nghiệm thực của phương trình là:
Câu 8:
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân, cạnh huyền bằng . Thể tích khối nón là:
Câu 9:
Cho khối lăng trụ đứng ABC.A'B'C' có BB'=a, đáy ABC là tam giác vuông cân tại B và AC = . Tính thể tích V của khối lăng trụ đã cho.
Câu 12:
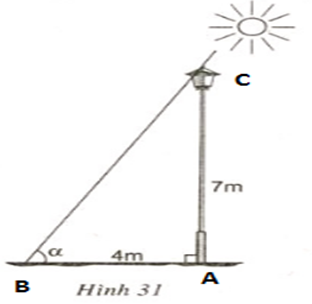
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc α trong hình 31)
Câu 14:
Mỗi tổ gồm 5 người đắp xong một đoạn đường trong 20 ngày. Hỏi nếu tổ đó chỉ có 4 người thì đắp xong đoạn đường đó trong bao nhiêu ngày? (Mức làm của mỗi người như nhau)
Câu 15:
Cho có . Tia phân giác của góc B cắt AC ở D, tia phân giác của góc C cắt AB ở E và cắt BD ở I. Chứng minh IE = ID