Câu hỏi:
18/07/2024 246
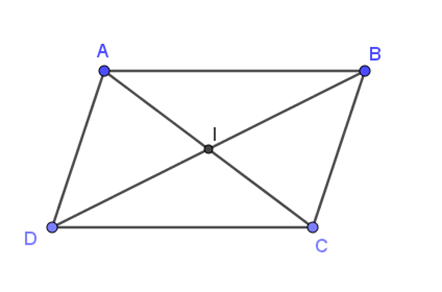
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
Cho hình bình hành ABCD với giao điểm hai đường chéo là I. Khi đó:
A. →AB−→AI=→BI;
A. →AB−→AI=→BI;
B. →AB−→DA=→BD;
B. →AB−→DA=→BD;
C. →AB−→DC=→0;
C. →AB−→DC=→0;
D. →AB−→DB=→0.
D. →AB−→DB=→0.
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
+) Ta có: →AB−→AI=→IB≠→BI nên A sai.
+) →AB−→DA=→AB+→AD=→AC≠→BD (theo quy tắc hình bình hành) nên B sai.
+) Ta có: →AB−→DC=→AB+→CD
Mà →BA=→CD (do ABCD là hình bình hành)
Vậy →AB−→DC=→AB+→CD=→AB+→BA=→AA=→0. Nên C đúng.
+) Ta có: →AB−→DB=→AB+→BD=→AD≠→0. Vậy D sai.
Đáp án đúng là: C
+) Ta có: →AB−→AI=→IB≠→BI nên A sai.
+) →AB−→DA=→AB+→AD=→AC≠→BD (theo quy tắc hình bình hành) nên B sai.
+) Ta có: →AB−→DC=→AB+→CD
Mà →BA=→CD (do ABCD là hình bình hành)
Vậy →AB−→DC=→AB+→CD=→AB+→BA=→AA=→0. Nên C đúng.
+) Ta có: →AB−→DB=→AB+→BD=→AD≠→0. Vậy D sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 2) và B(3; – 1). Độ dài vectơ →AB là:
Trong mặt phẳng tọa độ Oxy, cho điểm A(1; 2) và B(3; – 1). Độ dài vectơ →AB là:
Câu 2:
Hãy viết số quy tròn của số gần đúng a = 15,318 biết ¯a = 15,318 ± 0,05.
Hãy viết số quy tròn của số gần đúng a = 15,318 biết ¯a = 15,318 ± 0,05.
Câu 3:
Cho tam giác ABC vuông tại A có AB = a, AC = 2a. Gọi M là trung điểm của BC, điểm D thuộc AC sao cho AD=a2. Chứng minh rằng BD vuông góc với AM.
Câu 4:
Trong mặt phẳng tọa độ, cho →u=3→i−5→j. Khi đó tọa độ của vectơ →u là
Trong mặt phẳng tọa độ, cho →u=3→i−5→j. Khi đó tọa độ của vectơ →u là
Câu 5:
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính (→CB,→CA).
Cho tam giác ABC vuông tại A có: AB = 4, BC = 8. Tính (→CB,→CA).
Câu 6:
Cho hai vectơ →a và →b đều khác →0. Biết: (→a,→b)=30∘, →a.→b=√3và |→b|=2. Tính độ dài của vectơ →a.
Cho hai vectơ →a và →b đều khác →0. Biết: (→a,→b)=30∘, →a.→b=√3và |→b|=2. Tính độ dài của vectơ →a.
Câu 7:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích →AN qua các vectơ →a và →b ta được biểu thức là:
Cho tam giác ABC. Đặt →AB=→a, →AC=→b. M thuộc cạnh AB sao cho AB = 3AM, N thuộc tia BC và CN = 2BC. Phân tích →AN qua các vectơ →a và →b ta được biểu thức là:
Câu 9:
Để làm đường điện dây cao thế ở Hà Giang từ vị trí bản A đến bản B, người ta phải tránh một ngọn núi nên người ta phải nối thẳng đường dây từ bản A đến bản C dài 12 km rồi nối từ bản C đến bản B dài 8 km. Qua đo đạc người ta xác định được ^ABC=65∘. Hỏi so với việc nối thẳng từ bản A đến bản B, người ta tốn thêm bao nhiêu tiền, biết mỗi km dây có giá 150 000 đồng.
Để làm đường điện dây cao thế ở Hà Giang từ vị trí bản A đến bản B, người ta phải tránh một ngọn núi nên người ta phải nối thẳng đường dây từ bản A đến bản C dài 12 km rồi nối từ bản C đến bản B dài 8 km. Qua đo đạc người ta xác định được ^ABC=65∘. Hỏi so với việc nối thẳng từ bản A đến bản B, người ta tốn thêm bao nhiêu tiền, biết mỗi km dây có giá 150 000 đồng.
Câu 10:
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
Cho tứ giác ABCD. Gọi E, F lần lượt là trung điểm của AB, CD, O là trung điểm của EF. Khẳng định nào sau đây là đúng ?
Câu 11:
Cho β là góc tù. Tìm khẳng định đúng trong các khẳng định dưới đây?
Cho β là góc tù. Tìm khẳng định đúng trong các khẳng định dưới đây?
Câu 15:
Cho mẫu số liệu sau:
24; 16; 12; 5; 9; 3.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
Cho mẫu số liệu sau:
24; 16; 12; 5; 9; 3.
Tìm độ lệch chuẩn của mẫu số liệu trên (làm tròn đến hàng phần trăm).
