Câu hỏi:
14/07/2024 146
Cho hệ bất phương trình {x≥0x−y−1≤0x+2y−10≤0. Diện tích miền nghiệm của hệ bất phương trình bằng:
A. 6;
B. 12;
C. 24;
D. 28.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.
Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d1: x = 0) chứa điểm (1; 0).
• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.
Vẽ đường thẳng d2: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).
Xét điểm O(0; 0) ∉ d2, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d2) chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.
Vẽ đường thẳng d3: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d3) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.
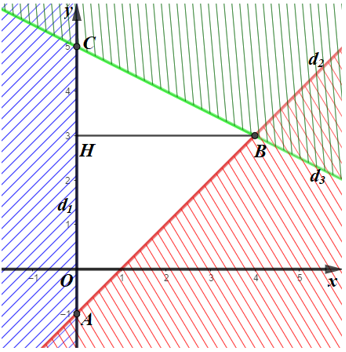
Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(–1; 0), B(4; 3) và C(0; 5).
Gọi BH là đường cao kẻ từ B đến AC.
Khi đó BH = |xB| = 4.
CA = CO + OA = |yC| + |yA| = 5 + 1 = 6.
Diện tích của tam giác ABC là:
S = 12 BH.CA = 12 .4.6 = 12 (đơn vị diện tích).
Vậy ta chọn phương án B.
Hướng dẫn giải
Đáp án đúng là: B
Trên mặt phẳng Oxy:
• Biểu diễn miền nghiệm của bất phương trình: x ≥ 0.
Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng (kể cả đường thẳng d1: x = 0) chứa điểm (1; 0).
• Biểu diễn miền nghiệm của bất phương trình: x – y – 1 ≤ 0.
Vẽ đường thẳng d2: x – y – 1 = 0 đi qua hai điểm (0; –1) và (1; 0).
Xét điểm O(0; 0) ∉ d2, ta có: 0 – 0 – 1 = –1 < 0 nên miền nghiệm của bất phương trình x – y – 1 ≥ 0 là nửa mặt phẳng (kể cả bờ d2) chứa điểm O(0; 0).
• Biểu diễn miền nghiệm của bất phương trình: x + 2y – 10 ≤ 0.
Vẽ đường thẳng d3: x + 2y – 10 = 0 đi qua hai điểm (0; 5) và (10; 0).
Xét điểm O(0; 0) ∉ d1, ta có: 0 + 2.0 – 10 = –10 < 0 nên miền nghiệm của bất phương trình x + 2y – 10 ≤ 0 là nửa mặt phẳng (kể cả bờ d3) chứa điểm O(0; 0).
Miền không gạch chéo (kể cả bờ d1, d2, d3) là giao của các miền nghiệm và cũng là phần biểu diễn miền nghiệm của hệ bất phương trình đã cho.

Miền nghiệm của hệ bất phương trình là miền tam giác ABC với A(–1; 0), B(4; 3) và C(0; 5).
Gọi BH là đường cao kẻ từ B đến AC.
Khi đó BH = |xB| = 4.
CA = CO + OA = |yC| + |yA| = 5 + 1 = 6.
Diện tích của tam giác ABC là:
S = 12 BH.CA = 12 .4.6 = 12 (đơn vị diện tích).
Vậy ta chọn phương án B.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Với giá trị nào của m thì điểm A(1 − m; m) không thuộc miền nghiệm của bất phương trình 2x − 3(y − x) > 4.
Câu 2:
Cho hệ bất phương trình {0≤y≤4x≥0x−y−1≤0x+2y−10≤0. Gọi điểm có toạ độ (x; y) thuộc miền nghiệm của hệ bất phương trình sao cho F(x; y) = x + 2y đạt giá trị lớn nhất. Số điểm thoả mãn là:
Câu 3:
Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 30 giây quảng cáo trên sóng phát thanh là 5 000 000 đồng, trên đài truyền hình là 15 000 000 đồng. Sóng phát thanh chỉ nhận phát các chương trình quảng cáo có thời lượng ít nhất là 30 giây và nhiều dài nhất 2 phút. Đài truyền hình chỉ nhận các chương trình quảng cáo có thời lượng ít nhất là 10 giây và nhiều nhất là 30 giây. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa 20 000 000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất?
Câu 4:
Tất cả các giá trị thực của tham số m để bất phương trình 3x + my − 7 ≥ 0 có miền nghiệm chứa điểm A(√2; 1) là:


