Cho hai đường thẳng d₁: 2x – 3y + 7 = 0 và d₂: 4x – 6y + 10 = 0. Chọn khẳng định đúng trong các khẳng định sau.

Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là

Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là 2 trong 8 điểm đó?

Cho hình dưới đây.

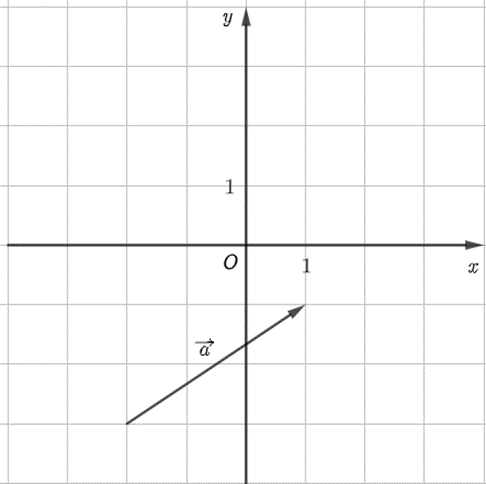
Tọa độ của vectơ \(\overrightarrow a \) trong hình vẽ trên là

Cho các điểm A(3; 7) và B(6; 1). Đường thẳng AB có phương trình là

Nếu một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện (các cách thực hiện của hai hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là

Trong mặt phẳng tọa độ Oxy, cho A(1; 1) và B(5; – 2). Độ dài đoạn thẳng AB là

Ở căn hộ chung cư nhà An người ta thường dùng các chữ số từ 0 đến 9 để thiết lập mật khẩu. Nhà An muốn thiết lập một mật khẩu gồm 4 chữ số khác nhau. Số cách thiết lập mật khẩu cho nhà An là

Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Viết phương trình đường trung trực của cạnh AB.

Góc giữa hai đường thẳng a: \(\sqrt 3 \)x – y + 7 = 0 và b: x – \(\sqrt 3 \)y – 2 = 0 là

Cho tập hợp A gồm n phần tử (n ∈ ℕ^*). Mỗi hoán vị của n phần tử đó là

Trong mặt phẳng tọa độ Oxy, cho M(2; – 1) và N(4; 1). Tọa độ vectơ \(\overrightarrow {NM} \) là

Một tổ có 12 học sinh, trong đó có một học sinh tên Châu. Có bao nhiêu cách chọn một nhóm gồm 5 người trong đó có học sinh tên Châu đi làm trực nhật?

Hệ số của x³ của khai triển (x – 1)⁴ là

Các thành phố A; B; C; D được nối với nhau bởi các con đường như hình vẽ sau:

Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?