Câu hỏi:
16/07/2024 272
Cho đồ thị (C):y=xx−1. Đường thẳng d đi qua điểm I(1; 1) cắt (C) tại hai điểm phân biệt A và B. Khi đó diện tích tam giác MAB với M(0; 3) đạt giá trị nhỏ nhất thì độ dài đoạn AB bằng:
Cho đồ thị (C):y=xx−1. Đường thẳng d đi qua điểm I(1; 1) cắt (C) tại hai điểm phân biệt A và B. Khi đó diện tích tam giác MAB với M(0; 3) đạt giá trị nhỏ nhất thì độ dài đoạn AB bằng:
A. √10
B. √6
C. 2√2
D. 2√3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Sử dụng: Vì I là tâm đối xứng của đồ thị hàm số y=xx−1⇒IA=IB.
- Chứng minh SΔMAB=2SΔMAI
- Kẻ AH⊥MI(H∈MI) ta có SΔMAI=12AH.MI, chứng minh để SΔMAB đạt giá trị nhỏ nhất thì SΔMAI đạt giá trị nhỏ nhất ⇒AH đạt giá trị nhỏ nhất.
- Viết phương trình đường thẳng MI, tính AH=d(A;MI), sử dụng BĐT Cô-si để tìm GTNN.
- Suy ra tọa độ điểm A tính IA và suy ra AB
Cách giải:
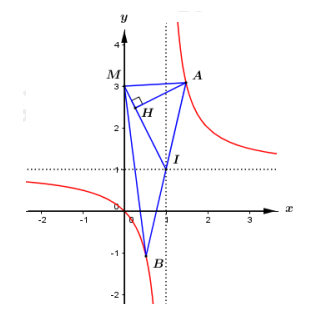
Dễ thấy I là tâm đối xứng của đồ thị hàm số y=xx−1 (giao điểm 2 đường tiệm cận).
Vì d đi qua A và cắt đồ thị y=xx−1 tại 2 điểm phân biệt A, B nên IA=IB=12AB.
Ta có: SΔMAISΔMAB=MIMA=12⇒SΔMAB=2SΔMAI
Kẻ AH⊥MI(H∈MI) ta có SΔMAI=12AH.MI với MI=√(1−0)2+(1−3)2=√5
⇒SΔMAI=12AH.√5=√52AH.
Để SΔMAB đạt giá trị nhỏ nhất thì SΔMAI đạt giá trị nhỏ nhất ⇒AH đạt giá trị nhỏ nhất.
Phương trình đường thẳng MI là x−10−1=y−13−1⇔2(x−1)=−(y−1)⇔2x+y−3=0
Gọi A(x0;x0x0−1)∈(C) ta có AH=d(A;MI)=|2x0+x0x0−1−3|√22+12=|2x0+1x0−1−2|√5.
Giả sử A là điểm nằm bên phải đường thẳng x>1⇒x0>1.
Áp dụng BĐT Cô-si ta có: 2x0+1x0−1−2=2(x0−1)+1x0−1≥2√2⇒AHmin=2√2√5=2√105.
Dấu “=” xảy ra ⇔2(x0−1)=1x0−1⇔(x0−1)2=12⇔x0−1=1√2⇔x0=1+1√2.
Khi đó A(1+1√2;1+√2)⇒IA=√(1+1√2−1)2+(1+√2−1)2=√102⇒AB=2IA=√10.
Vậy để SΔMAB đạt giá trị nhỏ nhất thì AB=√10.
Chọn A.
Phương pháp:
- Sử dụng: Vì I là tâm đối xứng của đồ thị hàm số y=xx−1⇒IA=IB.
- Chứng minh SΔMAB=2SΔMAI
- Kẻ AH⊥MI(H∈MI) ta có SΔMAI=12AH.MI, chứng minh để SΔMAB đạt giá trị nhỏ nhất thì SΔMAI đạt giá trị nhỏ nhất ⇒AH đạt giá trị nhỏ nhất.
- Viết phương trình đường thẳng MI, tính AH=d(A;MI), sử dụng BĐT Cô-si để tìm GTNN.
- Suy ra tọa độ điểm A tính IA và suy ra AB
Cách giải:

Dễ thấy I là tâm đối xứng của đồ thị hàm số y=xx−1 (giao điểm 2 đường tiệm cận).
Vì d đi qua A và cắt đồ thị y=xx−1 tại 2 điểm phân biệt A, B nên IA=IB=12AB.
Ta có: SΔMAISΔMAB=MIMA=12⇒SΔMAB=2SΔMAI
Kẻ AH⊥MI(H∈MI) ta có SΔMAI=12AH.MI với MI=√(1−0)2+(1−3)2=√5
⇒SΔMAI=12AH.√5=√52AH.
Để SΔMAB đạt giá trị nhỏ nhất thì SΔMAI đạt giá trị nhỏ nhất ⇒AH đạt giá trị nhỏ nhất.
Phương trình đường thẳng MI là x−10−1=y−13−1⇔2(x−1)=−(y−1)⇔2x+y−3=0
Gọi A(x0;x0x0−1)∈(C) ta có AH=d(A;MI)=|2x0+x0x0−1−3|√22+12=|2x0+1x0−1−2|√5.
Giả sử A là điểm nằm bên phải đường thẳng x>1⇒x0>1.
Áp dụng BĐT Cô-si ta có: 2x0+1x0−1−2=2(x0−1)+1x0−1≥2√2⇒AHmin=2√2√5=2√105.
Dấu “=” xảy ra ⇔2(x0−1)=1x0−1⇔(x0−1)2=12⇔x0−1=1√2⇔x0=1+1√2.
Khi đó A(1+1√2;1+√2)⇒IA=√(1+1√2−1)2+(1+√2−1)2=√102⇒AB=2IA=√10.
Vậy để SΔMAB đạt giá trị nhỏ nhất thì AB=√10.
Chọn A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Một khối trụ có đường cao bằng 2, chu vi thiết diện qua trục gấp 3 lần đường kính đáy. Thể tích của khối trụ đó bằng:
Câu 5:
Có 10 học sinh, gồm 5 bạn lớp 12A và 5 bạn lớp 12B tham gia một trò chơi. Để thực hiện trò chơi, người điều khiển ghép ngẫu nhiên 10 học sinh đó thành 5 cặp. Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng
Câu 6:
Có bao nhiêu số nguyên a để phương trình z2−(a−3)z+a2+a=0 có hai nghiệm phức z1,z2 thỏa mãn |z1+z2|=|z1−z2|.
Có bao nhiêu số nguyên a để phương trình z2−(a−3)z+a2+a=0 có hai nghiệm phức z1,z2 thỏa mãn |z1+z2|=|z1−z2|.
Câu 7:
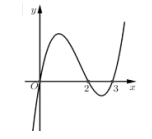
Giả sử f(x) là một đa thức bậc bốn. Đồ thị hàm số y = f'(1 - x) được cho như hình bên. Hỏi đồ thị hàm số g(x)=f(x2−3) nghịch biến trên khoảng nào trong các khoảng sau?

Câu 8:
Giả sử f(x) là một hàm số có đạo hàm liên tục trên ℝ. Biết rằng G(x)=x3 là một nguyên hàm của g(x)=e−2xf(x) trên ℝ.Họ tất cả các nguyên hàm của hàm số e−2xf' là:
Câu 9:
Giả sử f(x) là hàm liên tục trên và diện tích hình phẳng được kẻ sọc ở hình bên bằng 3. Tích phân bằng:
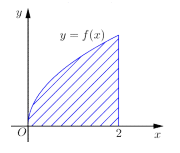
Giả sử f(x) là hàm liên tục trên và diện tích hình phẳng được kẻ sọc ở hình bên bằng 3. Tích phân bằng:

Câu 10:
Cho hình lập phương ABCD.A'B'C'D'. Góc giữa hai đường thẳng AB và B'D' bằng:
Câu 11:
Cho góc ở đỉnh của một hình nón bằng Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
Cho góc ở đỉnh của một hình nón bằng Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
Câu 13:
Hàm số y = sin x đồng biến trên khoảng nào trong các khoảng sau:
Hàm số y = sin x đồng biến trên khoảng nào trong các khoảng sau:
Câu 14:
Có bao nhiêu số nguyên a để phương trình có hai nghiệm thực phân biệt.
Có bao nhiêu số nguyên a để phương trình có hai nghiệm thực phân biệt.
Câu 15:
Cho hàm số y = f(x) liên tục trên và có bảng xét dấu đạo hàm như hình bên. Hỏi hàm số đã cho có bao nhiêu điểm cực trị?

Cho hàm số y = f(x) liên tục trên và có bảng xét dấu đạo hàm như hình bên. Hỏi hàm số đã cho có bao nhiêu điểm cực trị?




![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)